Метод узловых напряжений (МУН)

Линейные резистивные цепи (РЛЦ)

РЛЦ - это цепи, содержащие зависимые и независимые источники и только резистивное сопротивление.

Методы анализа РЛЦ.

Метод эквивалентного преобразования (МЭП)

МЭП используется при расчете цепей с одним источником.

Схема 1 Схема 2

1. Определяем Rэкв относительно зажимов источника.

2. Вне схемы 1 определяем ток по закону Ома через источник, а для схемы 2 по закону Ома определяем напряжение U₁₂ на зажимах источника тока.

3. Определяем токи и напряжения в ветвях цепи по закону Ома и законам Киркгофа.

Метод наложения (МН)

 

МН основан на принципе наложения (суперпозиции), используется в цепях, содержащих не более трех источников. В цепях, содержащих более трех источников, расчет с помощью МН возможен, но расчеты неоправданно громоздки.

1. Нарисовать схемы с каждым источником в отдельности. При исключении источника остаются их внутренние сопротивления.(R_{внутр. ист тока}=∞, следовательно источник тока заменяют обрывом, R_{внутр. ист напряжения}=0, следовательно источник напряжения заменяют проводом).

2. Каждую схему решают с помощью МЭП, находят частичные токи и напряжения,

3. Нахождение токов и напряжений в заданной цепи путем алгебраического суммирования токов и напряжений.

 

Метод токов ветвей (МТВ)

 

Метод, в котором переменными системы уравнений являются токи в ветвях, метод основан на составлении уравнений по первому и второму законам Киркгофа.

Алгоритм:

1. Определить количество уравнений для расчета неизвестных токов в цепи

N_I= Nу-1

N_II= Nв –Nу+1-N_{ист. тока}

N= N_I+ N_II= Nв –-N_{ист. тока}

2. Произвольно показать направления токов ветвей (с учетом первого закона Киркгофа)

3. Выбрать независимые контуры, произвольно показать положительные направления обхода этих контуров и составить уравнения по второму закону Киркгофа

4. Решить полученную систему уравнений любым известным методом и определить токи ветвей

5. Сделать проверку с помощью первого закона Киркгофа или с помощью баланса мощностей

 

Цепи с U₀, R

1)

N_I= Nу-1

N_I= 4-1=3

N_II= Nв –Nу+1

N_II= 6 –4+1=3

N= N_I+ N_II

2) Произвольно покажем положительные направления течения токов, составим уравнения по первому закону Киркгофа

(1) I₁+I₂-I₄=0

(2) - I₂+I₅+I₃=0

(3) -I₃-I₁+I₆=0

3) Выбираем независимые контуры, произвольно показываем направления обхода и составляем уравнения по второму закону Киркгофа

Независимый контур – это контур, в котором есть хотя бы одна ветвь, не входящая в какой другой контур.

(1) I₁R₁+U₀₁+U₀₃- I₃R₃- I₂R₂=0

(2) I₄R₄+I₂R₂+I₅R₅+U₀₅ =0

(3) I₃R₃- U₀₃ +I₆R₆ - U₀₅ - I₅R₅=0

4) Решить систему полученных уравнений любым известным методом и определить токи ветвей

5) Сделать проверку с помощью первого закона Киркгофа или с помощью баланса мощностей

Цепи с U₀, R, i₀

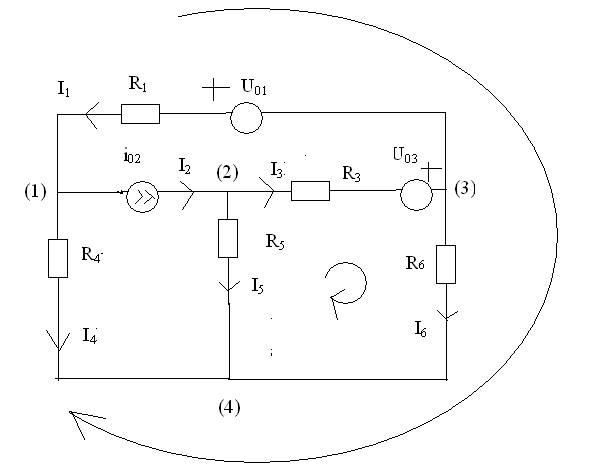
1)

N_I= Nу-1

N_I= 4-1=3

N_II= Nв –Nу+1-N_{ист. тока}

N_II= 6 –4+1-1=2

N= N_I+ N_II= Nв –-N_{ист. тока}

2) Произвольно покажем положительные направления течения токов, составим уравнения по первому закону Киркгофа

(1) i₀₂+I₄-I₁=0

(2) I₅+I₃- i₀₂=0

(3) I₁+I₆-I₃=0

3) Выбираем независимые контуры, произвольно показываем направления обхода и составляем уравнения по второму закону Киркгофа

(1) I₃R₃+ I₆R₆- U₀₆- I₅R₅ =0

(2) –I₁R₁- U₀₁ +I₆R₆ - U₀₆ - I₄R₄=0

4) Решить систему полученных уравнений любым известным методом и определить токи ветвей

Баланс мощностей

 

P_отд=P_потр Мощность отдаваемая равна мощности потребляемой.

P_потр=

P_отд= +

n-количество сопротивлений

m -количество источников напряжения

l -количество сопротивлений источников тока

погрешность ≤3%

-U₀₁I₁+U₀₆I₆+U₂₁i₀₂=I₁²R₁+ I₃²R₃+ I₄²R₄+ I₅²R₅+ I₆²R₆

U₂₁= I₅R₅- I₄R₄

Метод узловых напряжений (МУН)

МУН – метод, в котором переменными системы уравнений являются узловые напряжения. Основан на законе Ома и первом законе Киркгофа (алгебраическая сумма токов в ветвях, сходящихся к любому узлу ЭЦ, тождественно равна 0)

Узловые напряжения U_k - напряжения в узлах, рассчитанные относительно базисного (опорного) узла.

G=1/R

U₁=µ₁- µ₀= µ₁- 0= µ₁

U_k=µ_k- µ₀= µ₁- 0= µ_k

U_1k=µ₁- µ_k= µ₁-µ_k= U₁- U_k

I₁=U₁G₁₀

I_k=U_kG_k0

I_1k=U_1kG_1k =G_1k (U₁- U_k)

Цепи с i₀, R

1)

N_I= Nу-1

N_I= 4-1=3

2)

(1) i₀₁+ i₀₆-I₅-I₂=0

(2) -i₀₁- i₀₃+I₅+I₄=0

(3) i₀₃+ i₀₈-I₄+I₅ +I₇=0

I₂=U₂₁G_1k =G₂ (U₂- U₁)

I₄=U₂₃G₄ =G₄ (U₂- U₃)

I₅=U₃₁G₅ =G₅ (U₃- U₁)

I₇=U₃G₇ =G₄ (U₂- U₃)

Подставим переменные в уравнения

i₀₁+ i₀₆- G₂(U₂- U₁) - G₅ (U₃- U₁)=0

-i₀₁- i₀₃+ G₂(U₂- U₁)+ G₄ (U₂- U₃)=0

- G₄ (U₂- U₃) +i₀₃+ G₅ (U₃- U₁)+ U₃G₇+ i₀₈=0

Перегруппируем

U₁ (G₂+ G₅) - U₂ G₂- U₃G₅ =-i₀₁- i₀₆

-U₁ G₂ +U₂(G₂+ G₄)- U₃ G₄=i₀₁+ i₀₃

-U₁ G₅ - U₂ G₄+U₃(G₄+ G₅+G₆)=i₀₃ -i₀₈

Переходим к канонической системе узловых уравнений третьего порядка

U₁ G₁₁ - U₂ G₁₂- U₃G₁₃ =i₁₁

-U₁ G₂₁ +U₂G₂₂- U₃ G₂₃=i₂₂

-U₁ G₃₁- U₂ G₃₂+U₃G₃₃=i₃₃

Cобственная проводимость G_kk k-ого узла - алгебраическая сумма проводимостей в ветвях, сходящихся к k-ому узлу, всегда положительна

Взаимная проводимость G_ki - алгебраическая сумма проводимостей в ветвях между k-ым и i-ым узлами, при этом ветви не пересекают другие узлы, всегда отрицательна

G_ki= G_ik

Собственные токи источников i_kk -собственные токи в k-той ветви, создаваемые источником в данной ветви.

Узел отрицательное значение

Узел положительное значение

 

 

Цепи с U₀, R, i₀

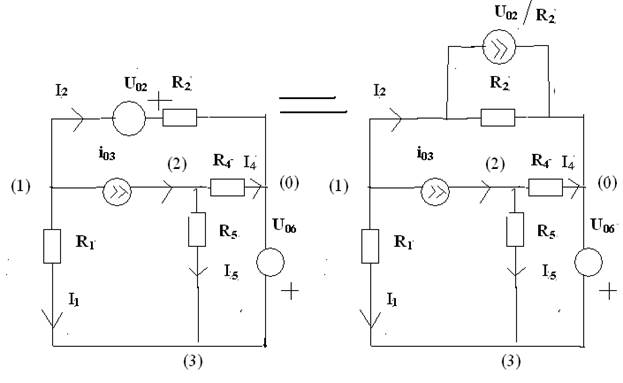
U₁(1/R₁+1/R₂)-U₂*0-U₃*1/R₁=-U₀₂*1/R₂-i₀₃

-U₁*0+U₂(1/R₄+1/R₅) -U₃*1/R₅=i₀₃

U₃=U₀₆

U₁(1/R₁+1/R₂) =-U₀₂*1/R₂-i₀₃+ U₀₆*1/R₁

U₂(1/R₄+1/R₅) =i₀₃ + U₀₆*1/R₅

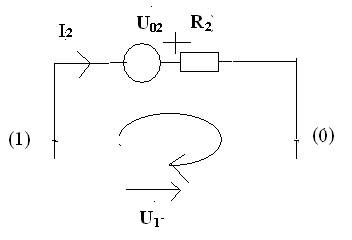
i₂R₂ -U₀₂- U₁=0 i₂=(U₀₂+ U₁)/ R₂ i_k=(U_вых+ U_вх ± U_0k)/ R_k

Ток, текущий через источник напряжения, находится по первому закону Киркгофа

Алгоритм:

1 Выбрать базисный узел (опорный узел): для цепей с источниками тока i₀ и с сопротивлениями – произвольно, для цепей с источниками тока i₀, источниками напряжения U₀ и с сопротивлениями выбрать один из узлов, к которому подключен источник напряжения.

2 Определить порядок системы уравнений N_I= Nу-1-N_{ист. тока}

3 Записать каноническую систему уравнений первого порядка

4 Рассчитать собственные проводимости G_kk, взаимные проводимости G_ki, собственные токи источников i_kk

5 Рассчитать узловые напряжения U_k

6 Рассчитать токи ветвей i_k по закону Ома

7 Осуществить проверку по балансу мощностей (или по первому закону Киркгофа)

 

МУН с зависимыми источниками

Зависимые источники – результат идеализации активных устройств(операционных усилителей, резисторов, ламп)

На первом этапе необходимо нарисовать схему замещения, где активный прибор заменяется зависимым четырехполюсником.

U₂=kU₃

U₁(1/R₁+1/R₂)-U₂*0-U₃*1/R₁=i₀

-U₁*1/R₂-U₂*1/R₃+U₃(1/R₂+1/R₃) =0

U₃=U₂/k

U₁(1/R₁+1/R₂)-U₂*1/(kR₂)=i₀

-U₁*1/R₂-U₂*1/(kR₃)+U₃(1/(kR₂)+1/(kR₃)-1/R₃) =0

U₂=Δ2/Δ

Δ=

Поделиться:

Воспользуйтесь поиском по сайту: