Тема: Смеси идеальных газов.

I. Понятие об идеальном газе. Состояние системы.

Предыдущая лекция была посвящена вопросам методов исследования свойств тел на основе молекулярно-кинетической теории.

Используя выводы рассмотренных вопросов, разберем основные законы для газов.

Все газы делятся на два основных вида:

 

Идеальным газом называется газ, удовлетворяющий следующим условиям:

1) размеры молекул пренебрежительно малы

2) соударения молекул происходят как соударения упругих шариков

3) между молекулами не проявляются силы взаимодействия

Пример идеального газа – сильно разряженные газы (не превышающие атмосферное в 100 раз) при не очень низких температурах.

Реальным газом называется газ, между молекулами которого существуют заметные силы межмолекулярного взаимодействия, и учитывается размер молекул.

Понятие об идеальном газе является практически удобной абстракцией. Такое понятие дало возможность построить молекулярно-кинетическую теорию, рассмотреть вопросы о вычислении теплоемкостей, явления переноса и др. В определенных границах выводы этой теории хорошо подтверждаются экспериментами.

Введем некоторые понятия, необходимые для рассмотрения вопросов лекции.

Термодинамическая система – совокупность макроскопических объектов, обменивающихся энергией в форме работы и в форме теплоты как друг с другом, так и с внешней средой. Макроскопические объекты – компоненты (число от 1 до ¥).

 

Состояние системы определяется, как уже говорилось совокупностью её термодинамических параметров (параметров состояния).

 

Время перехода системы из неравновесного состояния в равновесное называется временем релаксации.

Термодинамическим процессом (процессом) называется всякое изменение состояния системы.

II. Процессы.

	1) Равновесный, при котором система проходит непрерывный ряд равновесных состояний: Этот процесс бесконечно медленный
	2) Обратимый, при котором возможно осуществить обратный переход через те же промежуточные состояния так, чтобы не осталось никаких изменений в окружающих телах. Пример: колебания тяжелого маятника. Необратимый, при котором в теле или в окружающих телах есть изменения. Примеры: передача тепла от более нагретого тела к менее нагретому; любой процесс с трением.
	3) Круговой (цикл), в результате совершения которого система возвращается в исходное состояние.

4) Адиабатный, осуществляемый системой без теплообмена с внешней средой.

5) Политропный, при котором идеальная теплоемкость газа постоянна (общий процесс, его частными случаями являются адиабатный и все изопроцессы).

6) Изопроцессы, протекающие при неизменном значении какого-либо параметра состояния при m = const.

 

III. Основные газовые законы.

Из основного уравнения кинетической теории газов можно вывести все газовые законы, ранее установленные экспериментально. Для вывода каждого закона используем конкретную формулу основного уравнения.

а) Закон Бойля-Мариотта (изотермический процесс)
	, т.к. , получим основное уравнение: , (из уравнения (8) лекции 7), где N – число молекул в единице объема m – масса газа – средняя квадратичная скорость молекул при t = const и m = const, следовательно, правая часть const, т.е. PV = const (1)
б) закон Гей-Люссака (изобарический процесс)
	(*) (**) поделив (*) на (**), получим: (2) или Vt = V0(1+ αt0), где Vt – температура при t0C; V0 – температура при 00С; – температурный коэффициент

в) Закон Шарля (изохорический процесс)

Получается аналогичным рассуждением:

(3)

или P_t = Р₀(1 + αt₀)

г) Объединенный газовый закон

(4)

Во всех выше рассмотренных законах масса газа считается постоянной.

Для примера приведем графики различных процессов в разных системах координат:

 

 

 

IV. Уравнение состояния идеальных газов и газовая постоянная.

Уравнением состояния газа называется уравнение, связывающее основные параметры, характеризующие состояние газа.

Согласно объединенному газовому закону

,

где С – газовая постоянная.

С зависит от массы, химического состава и выбора единиц измерения P, V, T.

– называется удельная газовая постоянная.

Получим уравнение, выведенное Клапейроном в 1834г. для произвольной массы газа:

PV=mBT (5)

B для системы СИ: ,

где ρ – плотность газа.

Однако гораздо удобнее пользоваться уравнением состояния в универсальном виде, что и было сделано Менделеевым в 1874г.

– уравнение Менделеева-Клапейрона, (6)

где μ – масса киломоля газа;

R – универсальная газовая постоянная.

R = 8,32∙10³ Дж/Кмоль∙К

или R = 8,32 ДЖ/моль∙К

– число молей.

Выясним физический смысл универсальной газовой постоянной. В цилиндре заключен 1 моль газа. Нагреваем газ на 10 при Р = const. Вычислим работу расширения газа. A = F(ℓ1– ℓ) = ps(ℓ1– ℓ)= pV1–pV = R(T + 1) – RT = R A = R (7)

Физический смысл R: R численно равна работе при изобарическом расширении 1 моля газа при нагревании его на 1 градус.

Уравнение Менделеева-Клапейрона широко используется для решения многих практических задач (вплоть до давлений, немного превышающих атмосферное и не очень низких температурах).

V. Смесь газов. Закон Дальтона.

Все зависимости, полученные выше для идеальных газов, справедливы и для их смесей, если в них подставлять газо­вую постоянную, молекулярную массу и теплоемкость смеси.

Закон Дальтона. В инженерной прак­тике часто приходится иметь дело с газо­образными веществами, близкими по свойствам к идеальным газам и пред­ставляющими собой механическую смесь отдельных компонентов различных газов, химически не реагирующих между собой. Это так называемые газовые сме­си. В качестве примера можно назвать продукты сгорания топлива в двигателях внутреннего сгорания, топках печей и па­ровых котлов, влажный воздух в сушиль­ных установках и т. п.

Основным законом, определяющим поведение газовой смеси, является закон Дальтона: полное давление смеси иде­альных газов равно сумме парциальных давлений всех входящих в нее компо­нентов:

Парциальное давление pi — давление, которое имел бы газ, если бы он один при той же температуре занимал весь объем смеси.

Способы задания смеси. Состав га­зовой смеси может быть задан массовы­ми, объемными или мольными долями.

Массовой долей называется отношение массы отдельного компонента Мi, к массе смеси М:

.

Очевидно, что и .

Массовые доли часто задаются в процентах. Например, для сухого воздуха ; .

Объемная доля представляет собой отношение приведенного объема газа V, к полному объему смеси V: .

Приведенным называется объем, который занимал бы компонент газа, ес­ли бы его давление и температура равня­лись давлению и температуре смеси.

Для вычисления приведенного объема запишем два уравнения состоя­ния i -го компонента:

; (2.1)

.

Первое уравнение относится к состоянию компонента газа в Смеси, когда он имеет парциальное давление pi и занимает пол­ный объем смеси, а второе уравнение — к приведенному состоянию, когда давле­ние и температура компонента равны, как и для смеси, р и Т. Из уравнений следует, что

. (2.2)

Просуммировав соотношение (2.2) для всех компонентов смеси, получим с учетом закона Дальтона ,откуда . Объемные доли также часто задаются в процентах. Для воз­духа , .

Иногда бывает удобнее задать со­став смеси мольными долями. Моль­ной долей называется отношение количества молей Ni рассматриваемого компонента к общему количеству молей смеси N.

Пусть газовая смесь состоит из N1 молей первого компонента, N2 молей вто­рого компонента и т. д. Число молей смеси , а мольная доля компонента будет равна .

В соответствии с законом Авогадро объемы моля любого газа при одинако­вых р и Т, в частности при температуре и давлении смеси, в идеально газовом состоянии одинаковы. Поэтому приве­денный объем любого компонента может быть вычислен как произведение объема моля на число молей этого компо­нента, т. е. а объем смеси — по формуле . Тогда , и, следовательно, задание смесильных газов мольными долями равно заданию ее объемными долями.

Газовая постоянная смеси газов. Просуммировавуравнения (2.1) для всех компонен­тов смеси, получим . Учитывая , можно записать

, (2.3)

где

. (2.4)

Из уравнения (2.3) следует, что смесь идеальных газов также подчиняется уравнению Клапейрона. Поскольку то из (2.4) следует, что газовая постоянная смеси [Дж/(кг-К)] имеет вид

(2.5)

Кажущаяся молекулярная масса смеси. Выразим формально газовую постоянную смеси R, введя кажущуюся окулярную массу смеси : (2.6)

Сравнивая правые части соотношений (2.5) и (2.6), найдем

.

Изопределения массовых долей следует, что

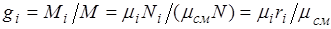
Просуммировав это соотношение для всех компонентов и учитывая, что , получим выражение для кажущейся молекулярной и массы смеси, заданной объемными долями:

. (2.7)

Соотношение между объемными и массо­выми долями. Учитывая (2.7), получаем .

Поскольку , то

Разделив числитель и знаменатель этой формулы на массу смеси М, получим

.

Аналитическое выражение первого закона термодинамики

Первый закон термодинамики пред­ставляет собой частный случай всеобще­го закона сохранения и превращения энергии применительно к тепловым явле­ниям. В соответствии с уравнением Эйн­штейна надо рассматривать единый закон сохранения и превращения массы и энергии. Однако в технической термодинамике мы имеем дело со столь малыми скоростями объекта, что дефект массы равен нулю, и поэтому закон со­хранения энергии можно рассматривать независимо.

Закон сохранения и превращения энергии является фундаментальным за­коном природы, который получен на ос­нове обобщения огромного количества экспериментальных данных и применим ко всем явлениям природы. Он утвер­ждает, что энергия не исчезает и не воз­никает вновь, она лишь переходит из одной формы в другую, причем убыль энергии одного вида дает эквивалентное количество энергии другого вида.

В числе первых ученых, утверждав­ших принцип сохранения материи и энер­гии, был наш соотечественник М. В. Ло­моносов (1711 — 1765 гг.).

Пусть некоторому рабочему телу с объемом V и массой М, имеющему тем­пературу Т и давление р, сообщается из­вне бесконечно малое количество тепло­ты . В результате подвода теплоты тело нагревается на dT и увеличивается в объеме на dV.

Повышение температуры тела свиде­тельствует об увеличении кинетической энергии его частиц. Увеличение объема тела приводит к изменению потенциаль­ной энергии частиц. В результате внут­ренняя энергия тела увеличивается на dU. Поскольку рабочее тело окружено средой, которая оказывает на него дав­ление, то при расширении оно произво­дит механическую работу против сил внешнего давления. Так как никаких других изменений в системе не происхо­дит, то по закону сохранения энергии

(2.8)

т. е. теплота, сообщаемая системе, идет на приращение ее внутренней энергии и на совершение внешней работы.

Полученное уравнение является ма­тематическим выражением первого зако­на термодинамики. Каждый из трех чле­нов этого соотношения может быть поло­жительным, отрицательным или равным нулю. Рассмотрим некоторые частные случаи.

1. — теплообмен системы с ок­ружающей средой отсутствует, т. е. теп­лота к системе не подводится и от нее не отводится. Процесс без теплообмена на­зывается адиабатным. Для него уравнение (2.8) принимает вид:

.

Следовательно, работа расширения, совершаемая системой в адиабатном процессе, равна уменьшению внутренней энергии данной системы. При адиабат­ном сжатии рабочего тела затрачивае­мая извне работа целиком идет на увели­чение внутренней энергии системы.

2. — при этом объем тела не изменяется, dV =0. Такой процесс на­зывается изохорным, для него

,

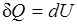т. е. количество теплоты, подведенное к системе при постоянном объеме, равно увеличению внутренней энергии данной системы.

3. dU=0 – внутренняя энергия системы не изменяется и

,

т.е. сообщаемая системе теплота пре­вращается в эквивалентную ей внешнюю работу.

Для системы, содержащей 1 кг рабо­чего тела

. (2.9)

Проинтегрировав уравнения (2.8) и (2.9) для некоторого процесса, полу­чим выражение первого закона термоди­намики в интегральной форме:

; .

Поделиться:

Воспользуйтесь поиском по сайту: