Комплексная огибающая. Векторное представление сигнала

Общая запись для полосового радиосигнала. Комплексная огибающая

Полосовые радиосигналы. Виды модуляции

При передаче информации в радиотехнике используются полосовые радиосигналы. Введем несколько понятий, для строгости рассуждений. Модулирующим сигналом будем называть низкочастотный информационный сигнал (речь, цифровая информация и т.д.), который требуется передать на частоте , где - верхняя частота спектра модулирующего сигнала. Полосовыми сигналами назовем сигналы, чьи спектры сосредоточены в некоторой полосе около несущей частоты . На рисунке 1 наглядно приведены спектры вещественного модулирующего (красный) и полосового (синий) сигналов.

 

Рисунок 1: Спектр модулирующего и полосового сигналов

 

Поскольку сигналы вещественные, то их спектры симметричны относительно нулевой частоты. Перенос модулирующего сигнала на несущую частоту называется модуляцией.

Рассмотрим способы модуляции, для этого рассмотрим несущее колебание :

(1)

где 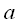- амплитуда несущего колебания, - начальная фаза. Также можно ввести понятие полной фазы несущего колебания:

(2)

а также мгновенной частоты сигнала, как производную от полной фазы:

(3)

Мгновенная частота несущего сигнала — постоянная величина равная . Таким образом при модуляции мы можем управлять всего двумя параметрами несущего колебания: амплитудой и полной фазой. При управлении только амплитудой получим амплитудную модуляцию и все ее производные, при управлении полной фазой получим угловую модуляцию (фазовая и частотная). При управлении и амплитудой и полной фазой можно получить все известные виды модуляции. Теперь можно рассмотреть общую запись полосового сигнала:

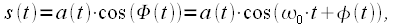
(4)

где — закон изменения амплитуды несущего колебания, а — изменение фазы несущего колебания в соответствии в с модулирующим сигналом.

 

Комплексная огибающая. Векторное представление сигнала

Введем понятие комплексной огибающей и векторного представления сигнала. Для этого рассмотрим комплексный сигнал

(5)

Из выражения (5) можно заметить, что 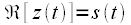, то есть реальная часть комплексного сигнала совпадает с полосовым радиосигналом. По формуле Эйлера можно представить:

(6)

Таким образом:

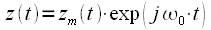
(7)

Выделенный сигнал носит название комплексной огибающей сигнала . Рассмотрим свойства этого сигнала. Сигнал является комплексным, с изменяющимися во времени амплитудой и фазой, причем изменение амплитуды сигнала полностью совпадает с изменением амплитуды радиосигнала , а изменение фазы полностью совпадает с изменением фазы радиосигнала . Однако отсутствие множителя говорит о том что сигнал представляет собой «перенесенный на нулевую частоту комплексный сигнал ». Комплексная огибающая сигнала существенно упрощает анализ сигнала.

Любое комплексное число можно представить в виде точки на комплексной плоскости или вектора выходящего из 0 до этой точки, а комплексный сигнал можно трактовать как комплексную функцию времени, т.е. вектор который описывает на комплексной плоскости некоторую траекторию в течении времени, как это показано на рисунке 2.

 

Рисунок 2: Векторное представление комплексного сигнала

 

Тогда комплексную экспоненту на комплексной плоскости можно представить вектором единичной амплитуды поворачивающегося за одну секунду на угол , совершая при этом оборотов в секунду. Таким образом при наблюдении за мы увидим окружность единичного радиуса которую вычерчивает вектор с частотой . При этом единичная окружность будет искажаться сигналом , а именно в течении времени вектор , будет менять амплитуду в соответствии с и скорость вращения в соответствии с . Так вот комплексная амплитуда позволяет нам остановить вращение вектора с частотой и посмотреть как меняется его амплитуда и фаза во время вращения. Это равносильно тому что ученый пытается рассмотреть муху когда она летает по комнате выписывая круги. Делать это не очень удобно, в то время как ее можно очень детально рассмотреть если поймать. Так же и комплексная огибающая это как бы пойманная неподвижная муха, мы можем детально изучить траекторию вектора комплексной огибающей.

Теперь вернемся к рассмотрению комплексной огибающей. можно представить в виде реальной и мнимой частей:

(8)

где - синфазная составляющая комплексной огибающей (или координата по оси абсцисс), а - квадратурная составляющая (или координата по оси ординат, как это показано на рисунке 3)

 

Рисунок 3: Векторное представление комплексной огибающей

 

Поделиться:

Воспользуйтесь поиском по сайту: