 |
Нахождение коэффициентов отражения и трансформации
|
|
|
|
Федеральное агентство по образованию РФ
Санкт-Петербургский Государственный электротехнический
университет “ЛЭТИ” им. В.И. Ульянова (Ленина)
Кафедра ЭУТ
Пояснительная записка
к курсовой работе по дисциплине:
“Волновые задачи акустики”
вариант № 3.1
Выполнил: студент Марусиченко В.А.
Преподаватель: Степанов Б.Г.
Санкт-Петербург
2009
Содержание
Исходные данные. 3
Введение. 4
Граничные условия. 5
Представление полей смещений и напряжений через потенциалы.. 5
Нахождение коэффициентов отражения и трансформации. 6
Численный анализ коэффициентов отражения и трансформации. 9
Графики коэффициентов отражения и трансформации. 11
Литература. 13
Исходные данные
Задание 3
Вариант 1
На бесконечную плоскую границу раздела двух сред 1 и 2, под углом θ, отсчитываемым от нормали к границе раздела, из среды 1 падает плоская поперечная гармоническая волна, поляризованная в плоскости падения.
1. Найти аналитическое выражение для коэффициентов отражения и прохождения по смещению.
2. Определить критические углы.
3. Получить аналитическое выражение для неоднородных волн.
4. Численно проанализировать модуль и фазу коэффициентов отражения и прохождения по смещению и по энергии в диапазоне углов падения от 0о до 90о.
Результаты расчетов представить в графической форме. Физические параметры рассматриваемых сред приведены в таблице 1.
Таблица 1
| Среда | ρ, кг/м3 | с l, м/с | с t, м/с | |
| Среда 1 | Сталь | |||
| Среда 2 | Вода | - |
Литература: Егоров Н.Н., Яковлев Л.А. «Колебания и волны» - Учебное пособие, изд. С-Пб ГЭТУ, С-Пб, 1997г.
|
|
|
Введение
При падении плоской поперечной волны, поляризованной в плоскости падения из твердого тела на бесконечную плоскую границу раздела твердая среда – жидкость порождается отраженная поперечная волна, поляризованная в плоскости падения, отраженная продольная волна и преломленная продольная волна. Задачу будем решать в терминах потенциалов смещения ( - скалярный потенциал смещения,
- скалярный потенциал смещения, 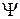 - векторный потенциал смещения). В соответствии с рис.1 опишем волны, участвующие в процессе отражения – преломления:
- векторный потенциал смещения). В соответствии с рис.1 опишем волны, участвующие в процессе отражения – преломления:
 (1)
(1)
где 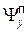 ,
,  - y- компоненты векторных потенциаловсмещения продольных падающей и отраженной волн соответственно,
- y- компоненты векторных потенциаловсмещения продольных падающей и отраженной волн соответственно, 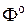 ,
, 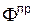 - скалярные потенциалы смещения продольных отраженной и преломленной волн соответственно,
- скалярные потенциалы смещения продольных отраженной и преломленной волн соответственно, 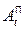 - амплитуда векторного потенциала падающей волны,
- амплитуда векторного потенциала падающей волны, 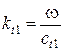 ,
,  ,
, 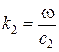 ,
,  - круговая частота,
- круговая частота, 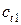 - скорость распространения поперечной волны в среде 1,
- скорость распространения поперечной волны в среде 1,  - скорость распространения продольной волны в среде 1,
- скорость распространения продольной волны в среде 1, 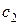 -скорость распространения продольной волны в среде 2,
-скорость распространения продольной волны в среде 2, 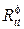 -коэффициент отражения поперечной волны по потенциалу,
-коэффициент отражения поперечной волны по потенциалу, 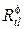 коэффициент трансформации падающей поперечной волны в отраженную продольную волну по потенциалу,
коэффициент трансформации падающей поперечной волны в отраженную продольную волну по потенциалу,  - коэффициент трансформации падающей поперечной волны в преломленную продольную волну по потенциалу,
- коэффициент трансформации падающей поперечной волны в преломленную продольную волну по потенциалу,

Процесс подчиняется закону Снеллиуса
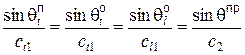 .
.
Следовательно,  .
.
Граничные условия
Запишем граничные условия:
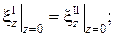 (2)
(2) 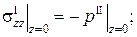 (3)
(3) 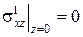 , (4)
, (4)
где  ,
, 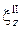 - проекции упругих смещений на ось z в средах 1 и 2 соответственно,
- проекции упругих смещений на ось z в средах 1 и 2 соответственно, 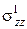 ,
, 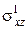 - упругие напряжения, возникающие в среде 1,
- упругие напряжения, возникающие в среде 1,  - давление, создаваемое в среде 2.
- давление, создаваемое в среде 2.
Представление полей смещений и напряжений через потенциалы
 (5)
(5)
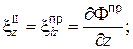 (6)
(6)
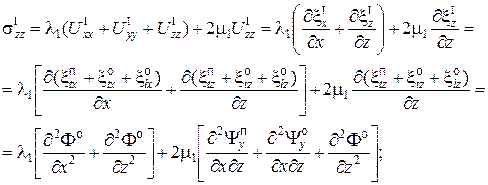 (7)
(7)
 (8)
(8)
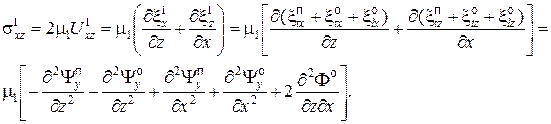 (9)
(9)
Нахождение коэффициентов отражения и трансформации
Подставив (1) в (5) – (9), а результаты этой подстановки в (2) – (4), получим систему уравнений:
 (10)
(10)
Решим систему уравнений методом Крамера:


Аналогично для 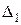 получим:
получим:
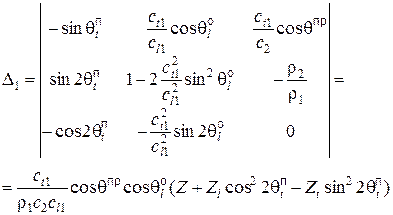
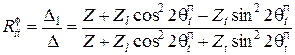 (11)
(11)
|
|
|

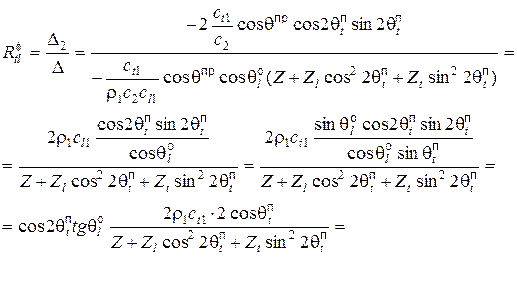
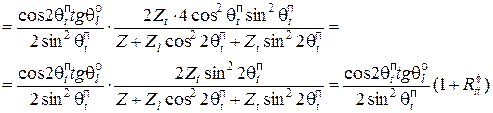
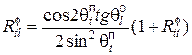 (12)
(12)
Выражение для коэффициента трансформации падающей поперечной волны в преломленную продольную волну по потенциалу найдем из системы уравнений (10):
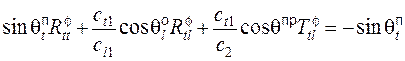
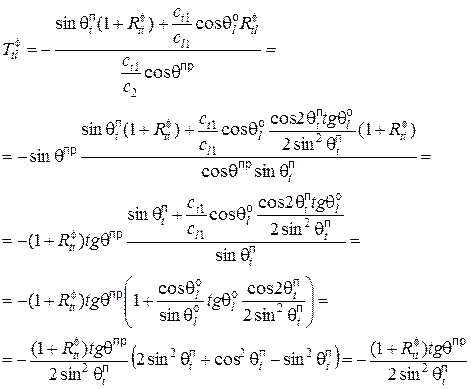
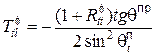 (13)
(13)
Коэффициенты отражения, трансформации и прохождения по смещения будут иметь вид:
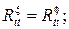 (14)
(14)
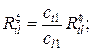 (15)
(15)
 (16)
(16)
Коэффициенты отражения, трансформации и прохождения по z-компоненте плотности потока энергии будут иметь вид:
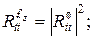 (17)
(17)
 (18)
(18)
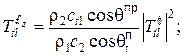 (19)
(19)
|
|
|


