 |
Меры информации синтаксического уровня
|
|
|
|
Количество и качество информации
Уровни проблем передачи информации
При реализации информационных процессов всегда происходит перенос информации в пространстве и времени от источника информации к приемнику (получателю) с помощью сигналов. Сигнал — физический процесс (явление), несущий сообщение (информацию) о событии или состоянии объекта наблюдения.
Сообщение — форма представления информации в виде совокупности знаков (символов), используемая для передачи.
Сообщение как совокупность знаков с точки зрения семиотики — науки, занимающейся исследованием свойств знаков и знаковых систем, — может изучаться на трех уровнях:
1) синтаксическом, где рассматриваются внутренние свойства сообщений, т. е. отношения между знаками, отражающие структуру данной знаковой системы.
2) семантическом, где анализируются отношения между знаками и обозначаемыми ими предметами, действиями, качествами, т. е. смысловое содержание сообщения, его отношение к источнику информации;
3) прагматическом, где рассматриваются отношения между сообщением и получателем, т. е. потребительское содержание сообщения, его отношение к получателю.
Проблемы синтаксического уровня касаются создания теоретических основ построения информационных систем. На этом уровне рассматривают проблемы доставки получателю сообщений как совокупности знаков, учитывая при этом тип носителя и способ представления информации, скорость передачи и обработки, размеры кодов представления информации, надежность и точность преобразования этих кодов и т. п., полностью абстрагируясь от смыслового содержания сообщений и их целевого предназначения. На этом уровне информацию, рассматриваемую только с синтаксических позиций, обычно называют данными, так как смысловая сторона при этом не имеет значения.
|
|
|
Проблемы семантического уровня связаны с формализацией и учетом смысла передаваемой информации, определения степени соответствия образа объекта и самого объекта. На данном уровне анализируются те сведения, которые отражает информация, рассматриваются смысловые связи, формируются понятия и представления, выявляется смысл, содержание информации, осуществляется ее обобщение.
На прагматическом уровне интересуют последствия от получения и использования данной информации потребителем. Проблемы этого уровня связаны с определением ценности и полезности использования информации при выработке потребителем решения для достижения своей цели. Основная сложность здесь состоит в том, что ценность, полезность информации может быть совершенно различной для различных получателей и, кроме того, она зависит от ряда факторов, таких, например, как своевременность ее доставки и использования.
Меры информации
Меры информации синтаксического уровня
Для измерения информации на синтаксическом уровне вводятся два параметра: объем информации (данных) – VД (объемный подход) и количество информации — I (энтропийный подход).
Объем информации VД. При реализации информационных процессов информация передается в виде сообщения, представляющего собой совокупность символов какого-либо алфавита. Если количество информации, содержащейся в сообщении из одного символа, принять за единицу, тообъем информации (данных) VД в любом другом сообщении будет равен количеству символов (разрядов) в этом сообщении.
Так, в десятичной системе счисления один разряд имеет вес, равный 10, и соответственно единицей измерения информации будет дит (десятичный разряд). В этом случае сообщение в виде n -разрядного числа имеет объем данных VД = п дит. Например, четырехразрядное число 2003 имеет объем данных VД = 4 дит.
|
|
|
В двоичной системе счисления один разряд имеет вес, равный 2, и соответственно единицей измерения информации будет бит (bit (binary digit) - двоичный разряд). В этом случае сообщение в виде n -разрядного числа имеет объем данных VД = п бит. Например, восьмиразрядный двоичный код 11001011 имеет объем данных VД = 8 бит.
В современной вычислительной технике наряду с минимальной единицей измерения данных бит широко используется укрупненная единица измерения байт, равная 8 бит. При работе с большими объемами информации для подсчета ее количества применяют более крупные единицы измерения, такие как килобайт (кбайт), мегабайт (Мбайт), гигабайт (Гбайт), терабайт (Тбайт):
1 кбайт = 1024 байт = 210 байт;
1 Мбайт = 1024 кбайт = 220 байт = 1 048 576 байт;
1 Гбайт = 1024 Мбайт = 230 байт = 1 073 741 824 байт;.
1 Тбайт = 1024 Гбайт = 240 байт = 1 099 511 627 776 байт.
Количество информации I (энтропийный подход). В теории информации и кодирования принят энтропийный подход к измерению информации. Этот подход основан на том, что факт получения информации всегда связан с уменьшением разнообразия или неопределенности (энтропии) системы. Исходя из этого количество информации в сообщении определяется как мера уменьшения неопределенности состояния данной системы после получения сообщения. Как только наблюдатель выявил что-нибудь в физической системе, энтропия системы снизилась, так как для наблюдателя система стала более упорядоченной.
Таким образом, при энтропийном подходе под информацией понимается количественная величина исчезнувшей в ходе какого-либо процесса (испытания, измерения и т. д.) неопределенности. При этом в качестве меры неопределенности вводится энтропия Н, и количество информации равно:
(2.1)
где Hapr — априорная энтропия о состоянии исследуемой системы;
Haps — апостериорная энтропия.
Апостериори — происходящее из опыта (испытания, измерения).
Априори — понятие, характеризующее знание, предшествующее опыту (испытанию), и независимое от него.
В случае, когда в ходе испытания имевшаяся неопределенность снята (получен конкретный результат, т. е. Haps = 0), количество полученной информации совпадает с первоначальной энтропией
|
|
|
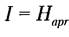
Рассмотрим в качестве исследуемой системы дискретный источник информации (источник дискретных сообщений), под которым будем понимать физическую систему, имеющую конечное множество возможных состояний. Это множество А = {a 1, a 2,..., ап} состояний системы в теории информации называют абстрактным алфавитом или алфавитом источника сообщений.
Отдельные состояния а1, а2,..., а„ называют буквами или символами алфавита.
Такая система может в каждый момент времени случайным образом принять одно из конечных множеств возможных состояний аi.
Поскольку одни состояния выбираются источником чаще, а другие реже, то в общем случае он характеризуется ансамблем А, т. е. полной совокупностью состояний с вероятностями их появления, составляющими в сумме единицу:
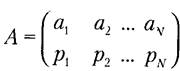, причем 
(2.2)
Введем меру неопределенности выбора состояния источника. Ее можно рассматривать и как меру количества информации, получаемой при полном устранении неопределенности относительно равновероятных состояний источника.
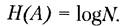(2.3)
Тогда при N = 1 получаем Н(А) = 0.
Указанная мера была предложена американским ученым Р. Хартли в 1928 г. Основание логарифма в формуле (2.3) не имеет принципиального значения и определяет только масштаб или единицу измерения В зависимости от основания логарифма применяют следующие единицы измерения.
1. Биты — при этом основание логарифма равно 2:
(2.4)
2. Ниты — при этом основание логарифма равно е:
3. Диты — при этом основание логарифма равно 10:
В информатике в качестве меры неопределенности обычно используют формулу (2.4). При этом единица неопределенности называется двоичной единицей, или битом, и представляет собой неопределенность выбора из двух равновероятных событий.
Формулу (2.4) можно получить эмпирически: для снятия неопределенности в ситуации из двух равновероятных событий необходим один опыт и соответственно один бит информации, при неопределенности, состоящей из четырех равновероятных событий, достаточно 2 бит информации, чтобы угадать искомый факт. Для определения карты из колоды, состоящей из 32 карт, достаточно 5 бит информации, т. е достаточно задать пять вопросов с ответами «да» или «нет», чтобы определить искомую карту.
|
|
|
Предложенная мера позволяет решать определенные практические задачи, когда все возможные состояния источника информации имеют одинаковую вероятность.
В общем случае степень неопределенности реализации состояния источника информации зависит не только от числа состояний, но и от вероятностей этих состояний. Если источник информации имеет, например, два возможных состояния с вероятностями 0,99 и 0,01, то неопределенность выбора у него значительно меньше, чем у источника, имеющего два равновероятных состояния, так как в этом случае результат практически предрешен (реализация состояния, вероятность которого равна 0,99).
Американский ученый К. Шеннон обобщил понятие меры неопределенности выбора H на случай, когда H зависит не только от числа состояний, но и от вероятностей этих состояний (вероятностей рi выбора символов аi, алфавита A). Эту меру, представляющую собой неопределенность, приходящуюся в среднем на одно состояние, называют энтропией дискретного источника информации:
(2.5)
Если снова ориентироваться на измерение неопределенности в двоичных единицах, то основание логарифма следует принять равным двум:
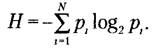(2.6)
При равновероятных выборах вероятность pi=1/N формула (2.6) преобразуется в формулу Р. Хартли (2.3):
Предложенная мера была названа энтропией не случайно. Дело в том, что формальная структура выражения (2.5) совпадает с энтропией физической системы, определенной ранее Больцманом.
Используя формулы (2.4) и (2.6), можно определить избыточность D алфавита источника сообщений А, которая показывает, насколько рационально применяются символы данного алфавита:
(2.7)
где Нmax(А) - максимально возможная энтропия, определяемая по формуле (2.4);
Н(А) — энтропия источника, определяемая по формуле (2.6).
Суть данной меры заключается в том, что при равновероятном выборе ту же информационную нагрузку на знак можно обеспечить, используя алфавит меньшего объема, чем в случае с неравновероятным выбором.
|
|
|
