 |
Вставить третье изображение.
|
|
|
|
Аналоги скоростей и ускорений
Аналоги скоростей и ускорений есть функции в удобной форме, позволяющие представить перемещение скорости и ускорения ведомых звеньев в зависимости от перемещения скоростей и ускорений ведущих звеньев.
Наиболее простой способ представить движение ведущего звена является функция: 
, 
.
В случае, если для звена R необходимо найти параметры движения, то можно записать формулу:
, где
– угловая скорость звена R; 
– угловая скорость ведущего звена;
t – время;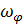 
– безразмерная угловая скорость или аналог угловой скорости.
Для функции ускорений можно продифференцировать последнее уравнение:
Аналогично могут быть получены уравнения для скоростей и ускорений какой-либо точки M и звена R. Из теоретической механики известно, что скорость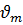 
и ускорение 
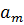могут быть получены последовательным дифференцированием радиус-вектора 
по времени.
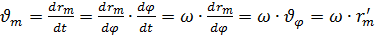, где
– угловая скорость ведущего звена; 
– аналог линейной скорости.
Дифференцируя по времени последнее уравнение получим ускорение 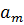. Это ускорение в общем случае состоит из четырех основных составляющих:
· Нормальное ускорение – направлено вдоль вектора к его началу.
· Касательное ускорение – перпендикулярно радиус-вектору .
· Относительное ускорение (релятивное) – направлено по радиусу .
· Ускорение Кориолиса – перпендикулярно радиусу .
Так как аналоги скорости и ускорения зависят только от обобщенных координат и не зависят от времени, то кинематическое исследование механизма можно вести чисто геометрическим способом.
Если ведущее звено движется с постоянной угловой скоростью (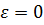
), то мы получим следующие уравнения:
|
|
|
Индекс П показывает, что движение перманентное или основное.
В случае, если в ранее приведенных формулах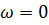 
, то и 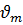также равны нулю, то мы получим движение, называемое начальным:
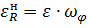
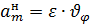
Любое движение звена может быть представлено как совокупность перманентного и начального движения звена:
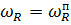
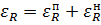
Определение положения звеньев и построение их траектории
Для определения положения звеньев и их точек необходимо иметь кинематическую схему механизма, а также закон изменения движения ведущего звена, а также момент времени, для которого происходит исследование.
Пусть необходимо определить положение механизма:
Вставить первое изображение.
Здесь присутствует основной механизм и дополнительная (присоединительная) группа FE. Основной механизм реализуется в виде кривошипно-шатунного (рычажного) механизма. Дополнительная (присоединительная) группа в данном случае группа 2(2). Звено 1 является входным. Для данного механизма степень подвижности равна 1.
Задано 
и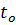 
. Подставив 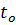в эту формулу найдём 
. В некоторых задачах может быть задана по условию.
Определение положений реализуется через план положений механизма, который в выбранном масштабе характеризуется самостоятельным механизмом.
Вставить второе изображение.
Дано: 
, 
, 
, 
, .
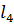1) Выбираем масштабный коэффициент плана и с учётом этого коэффициента проводим окружность радиуса AB из произвольно выбранной точки A.
Вставить третье изображение.
2) Выбираем систему координат таким образом, чтобы центр координат находился в точке A. Из условия работоспособности принимаем 
(
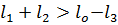) и откладываем точку D с учётом масштаба 
.
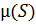3) Радиусом DC проводим из точки D окружность,
4) Их точки A под углом проводим прямую и получаем точку B.
5) Из точки B радиусом BC проводим окружность. Получаем две точки: 
и 
. В результате получаем два варианта исполнения основного механизма.
|
|
|
6) Путём принятия компромиссных решений выбирается какой-либо один вариант решения. Пусть это вариант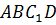 
.
7) Отмечаем точку F радиусом FE. Получаем точку E.
|
|
|
