Комплексная огибающая. Векторное представление сигнала

Введем понятие комплексной огибающей и векторного представления сигнала. Для этого рассмотрим комплексный сигнал

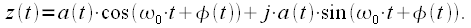
(5)

Из выражения (5) можно заметить, что , то есть реальная часть комплексного сигнала совпадает с полосовым радиосигналом. По формуле Эйлера можно представить:

(6)

Таким образом:

(7)

Выделенный сигнал носит название комплексной огибающей сигнала . Рассмотрим свойства этого сигнала. Сигнал 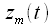является комплексным, с изменяющимися во времени амплитудой и фазой, причем изменение амплитуды сигнала 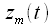полностью совпадает с изменением амплитуды радиосигнала , а изменение фазы полностью совпадает с изменением фазы радиосигнала . Однако отсутствие множителя говорит о том что сигнал 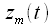представляет собой «перенесенный на нулевую частоту комплексный сигнал ». Комплексная огибающая сигнала существенно упрощает анализ сигнала.

Любое комплексное число можно представить в виде точки на комплексной плоскости или вектора выходящего из 0 до этой точки, а комплексный сигнал можно трактовать как комплексную функцию времени, т.е. вектор который описывает на комплексной плоскости некоторую траекторию в течении времени, как это показано на рисунке 2.

 

Рисунок 2: Векторное представление комплексного сигнала

 

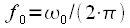Тогда комплексную экспоненту на комплексной плоскости можно представить вектором единичной амплитуды поворачивающегося за одну секунду на угол , совершая при этом оборотов в секунду. Таким образом при наблюдении за мы увидим окружность единичного радиуса которую вычерчивает вектор с частотой . При этом единичная окружность будет искажаться сигналом , а именно в течении времени вектор , будет менять амплитуду в соответствии с и скорость вращения в соответствии с . Так вот комплексная амплитуда позволяет нам остановить вращение вектора с частотой и посмотреть как меняется его амплитуда и фаза во время вращения. Это равносильно тому что ученый пытается рассмотреть муху когда она летает по комнате выписывая круги. Делать это не очень удобно, в то время как ее можно очень детально рассмотреть если поймать. Так же и комплексная огибающая это как бы пойманная неподвижная муха, мы можем детально изучить траекторию вектора комплексной огибающей.

Теперь вернемся к рассмотрению комплексной огибающей. 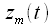можно представить в виде реальной и мнимой частей:

(8)

где 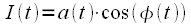- синфазная составляющая комплексной огибающей (или координата по оси абсцисс), а - квадратурная составляющая (или координата по оси ординат, как это показано на рисунке 3)

 

Рисунок 3: Векторное представление комплексной огибающей

 

 

Теорема найквиста.Формирующий фильтр.

Теорема Найквиста – Если синхронные короткие импульсы с частотой следования f_s символов в секунду податься в канал, имеющий идеальную прямоугольную частотную характеристику с частотой среза f_n= f_s/2 гц, отклики на эти импульсы можно наблюдать независимо, т.е без межсимвольных искажений

Пример искажений

На практике для передачи без мси надо не менее 1 Гц на 1 бит/с

Минимальная полоса канала связи на низкой частоте для дискретного канала ровна половине символьной скорости

Принцип работы фильтра - меняя импульсную характеристику формирующего фильтра мы можем сужать или расширять полосу сигнала

 

Формирующий фильтр Найквиста

Свойства h(t) необходимые для обеспечения минимальной ширины полосы передаваемого сигнала, рассмотрим b(t). Сигнал b(t) представляет собой последовательность дельта импульсов, соотвветствующих бит передаваемой инф. И отстоящих друг от друга на интервал Т/В

При прохождении формирующего фильтра очень важно, чтобы в моменты (т. е. в узлах дискретизации) было равно , как это показано на рисунке 5.

 

 

 

Тогда при демодуляции и декодировании можно исключить влияние МСИ, если производить оценку передаваемого бита точно в моменты времени , где точно соответствует передаваемой информации для всех бит.

 

Рисунок 6: Условия импульсной характеристики формирующего фильтра для исключения МСИ при декодировании

 

обеспечивать минимальную ширину полосы сформированного сигнала. Таковой импульсной характеристикой формирующего фильтра является

(7)

показанная на рисунке 7 (верхний график), которая соответствует идеальному ФНЧ с полосой (нижний график).

 

Рисунок 7: Импульсная характеристика идеального формирующего фильтра

 

Сигнал на выходе формирующего фильтра можно представить как отклик формирующего фильтра на входные дельта-импульсы соответствующие входному битовому потоку, что наглядно показано на рисунке 8.

 

Рисунок 8: Формирующий фильтр как интерполятор

 

На верхнем графике рисунка 8 каждый символ информации умножается на импульсную характеристику (7), тогда в узлах дискретизации импульсные характеристики от других информационных импульсов равны нулю и МСИ в моменты взятия отсутствует. По сути мы получили интерполятор в виде идеального ФНЧ, который «соединяет» плавной кривой, при этом сами не искажает.

 

 

Фильтр приподнятого косинуса

АЧХ фильтра «Приподнятый косинус»

а-Фактор скругления

Вблизи фронта идеальная АЧХ аппроксимируется функцией приподнятого Косинуса.а меняется от 0 до 1, а-задает интервал на котором происходит аппроксимация

а=0 идеальный ФНЧ

H(f)= f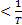

H(f)=0 f

 

 

а - регулирует степень сглаживания фронта АЧХ идеального фильтра, что соответствует уровню боковых лепестков импульсной характеристики . При а=1 АЧХ фильтра принимает вид приподнятого косинуса, а импульсная характеристика имеет минимальные боковые лепестки. Можно заметить, что полоса фильтра Найквиста по уровню 0.5 (-3 дБ) остается постоянной и равна .

 

 

 

Формирующий фильтр для согласованого приема сигнала.

dk dx

Для повышения помехоустойчивости систем применяют согласованную итерацию поэтому,

Фильтр приподнятого косинуса стоит на приеме

Фильтр корень из приподнятого косинуса стоит на передаче

Если импульсную характеристику этих фильтров сложить, то получиться функция приподнятого косинуса

АЧХ фильтра Корень из приподнятого косинуса

Для устранения МСИ ставят 2 таких фильтра.

 

17. Реальная спектральная эффективность ЦСРС

 

18. Структурные схемы модуляторов BFSK. Индекс модуляции для BFSK.

		несущей частоты.
	Г1 и Г2 (два генератора так как две несущих) ПК (преобразователь кода)   Наличие разрывов несущей частоты на границах max приводит к дискрет. спектра модул. сигнала, следовательно снижается спектральная эффективность. (применяется в низкоскоростных схемах, где спектральная эффективность не играет большой роли)

 

В лекциях(кратко) о индексе модуляции BFSK: m=∆ω/(2π(B/2)) =∆ω/πB Т.е. индекс модуляции показывает во сколько разнос несущих больше скорости передачи данных. По определению для частотной модуляции индекс модуляции равен отношению девиации несущей к верхней частоте модулирующего сигнала.

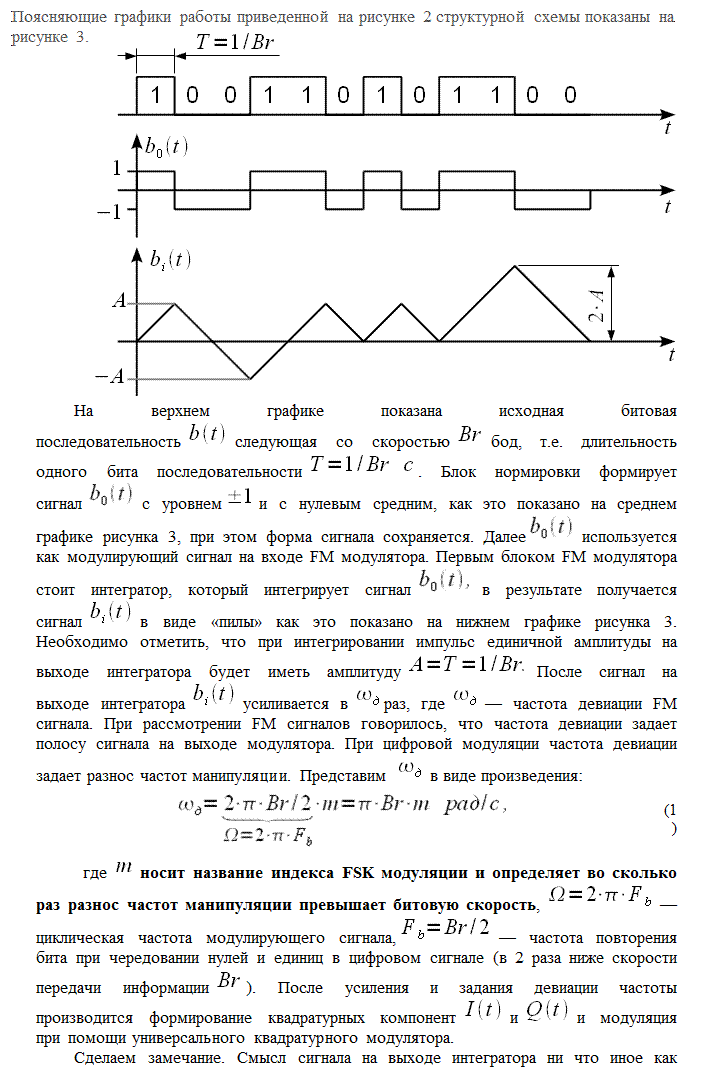
Вариант двоичной FSK модуляции,когда исходный модулирующий сигнал представляет собой двоичную бинарную последовательность нулей и единиц следующую с битовой скоростью 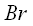. Формирователь FSK сигнала и принцип его функционирования можно условно представить, как это показано на рисунке

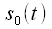На рисунке 1 показано два генератора, формирующие колебания и на различных частотах (смотри поясняющие осциллограммы рисунка 1). Также имеется электронный ключ, управляемый цифровым сигналом , таким образом, что при передаче логической «1» на выход подается сигнал , а при передаче логического «0» - сигнал . Таким образом, частота выходного сигнала «манипулируется» в зависимости от битовой последовательности. Не смотря на простоту приведенной схемы, она на практике не применяется, поскольку требуется очень быстродействующий ключ с минимальным переходным процессом, а также при произвольной начальной фазе генераторов возможны скачки по фазе при смене символа, что в свою очередь приводит к расширению спектра. На практике получила распространение FSK модуляция с непрерывной фазой CPFSK. Рассмотрим данный вид модуляции более подробно. FSK сигналы являются частным случаем сигналов с частотной модуляцией (FM) при модулирующем сигнале в виде двоичной битовой последовательности . Таким образом, для модуляции FSK можно использовать схему FM модулятора на базе универсального квадратурного модулятора, как это показано на рисунке 2.

 

 

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: