 |
Цифровая системотехника. Комбинационная логика
|
|
|
|
ЦЕЛЬ И ЗАДАЧИ РАБОТЫ
Целью данной лабораторной работы является изучение работы комбинационных схем, методов преобразования и упрощения цифровых схем при их реализации.
ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Цифровая электроника оперирует электрическими эквивалентами цифр. При этом числа чаще всего представляются в двоичной системе, в которой существуют только два знака: единица и нуль, им соответствуют сигналы “логическая единица” и “логический нуль”.
Теоретической основой цифровой схемотехники является булева алгебра или алгебра логики.
Основное понятие булевой алгебры – переключательная (булева) функция. Ее аргументы и она сама могут принимать только два значения: 0 и 1. С помощью булевых функций можно описать действие целого класса схем цифровой электроники, а также функционирование сочетаний этих схем. Такого рода схемы называются комбинационными, так как сигналы на выходе (1 или 0) определяются комбинацией сигналов на их входах (1 или 0).
Простейшими булевыми функциями являются функции одной переменной. Их может быть только 4:
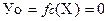 ;
;
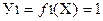 ;
;
 ;
;
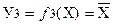 .
.
Эти функции описывают работу одновходных цифровых схем, а именно функции 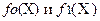 описывают схемы, выходы которых постоянно присоединены к уровням логического нуля и логической единицы соответственно; функция
описывают схемы, выходы которых постоянно присоединены к уровням логического нуля и логической единицы соответственно; функция  - схему, выход которой постоянно соединен с выходом. Функция
- схему, выход которой постоянно соединен с выходом. Функция  описывает инвертор, или схему отрицания (схема “НЕ”).
описывает инвертор, или схему отрицания (схема “НЕ”).
Если булева функция имеет две переменные, то в этом случае получается 16 видов функций. Запишем основные из них
 - конъюнкция;
- конъюнкция;
 - отрицательные конъюнкции;
- отрицательные конъюнкции;
 - дизъюнкция;
- дизъюнкция;
 - отрицательные дизъюнкции;
- отрицательные дизъюнкции;
Теорема. Булева функция любого количества переменных может быть
|
|
|
получена методом суперпозиции из функций двух переменных.
Метод суперпозиции состоит в подстановке на место переменных других булевых функций или пере нумерации переменных, т.е. в перестановке их местами.
Теорема позволяет ограничиться рассмотрением булевых функций только двух переменных и строить многовходовые комбинации схемы только из двухвходовых схем.
В булевой алгебре установлено, что любая булева функция двух переменных может быть получена из некоторого количества функций двух переменных. Набор функций двух переменных, из которого методом суперпозиции можно получить все остальные булевы функции двух переменных, а значит и все булевы функции любого числа переменных, называется функционально полным набором.
Примерами таких наборов являются У4 и У3, У6 и У3. Функционально полный набор представляет даже одна отрицательно взятая функция  или
или  .
.
Таким образом, на базе электронных схем одного типа, работа которых описывается, например, булевой функцией  или
или  можно построить любую цифровую комбинационную схему при условии, что выходы таких схем модно подключать ко входам других таких же схем.
можно построить любую цифровую комбинационную схему при условии, что выходы таких схем модно подключать ко входам других таких же схем.
Набор логических элементов, реально используемых в цифровой электронике, соответствует избыточно полному функциональному набору булевых функций. Избыточность набора позволяет получить несколько вариантов одинаково функционирующих схем и выбирать те из них, которые лучше подходят для решения конкретных задач.
Так, например, наиболее распространенное семейство цифровых интегральных микросхем 155 серии содержит 2 И-НЕ, НЕ, 2И, 2ИЛИ, 2ИЛИ-НЕ, 2И-НЕ, 8И-НЕ, 2-2И-2ИЛИ-НЕ.
ОБЪЕКТЫ ИССЛЕДОВАНИЯ И ОБОРУДОВАНИЕ
Объектами исследования в данной лабораторной работе являются логические элементы транзисторно-транзисторной логики:
2И-НЕ, 3И-НЕ, 2И-НЕ, 2-2И-2ИЛИ-НЕ (рисунок).
155ΛА3 155ΛА4 133ΛА1
|
|
|
 |
2И-НЕ 3И-НЕ 4И-НЕ
155ΛР1 155ΛА2
 |
2-2И-2ИЛИ-НЕ 8И-НЕ
основные параметры этих элементов приведены в табл.1.
| Рном МВт | U'вых В | Uºвых В | t  нс
нс
| t  нс
нс
| Краз | |
| 155ЛА1 155ЛА2 155ЛА3 155ЛА4 | 2,4 2,4 2,4 2,4 | 0,4 0,4 0,4 0,4 |
При выполнении работы используются лабораторный стенд типа УМ11 и осциллограф.
ЗАДАНИЕ НА РАБОТУ
Используя лабораторный стенд и осциллограф, рассмотреть работу основных логических элементов стенда и исследовать их основные параметры.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Подавая на входы элементов все возможные комбинации всех логических нулей и единиц, составьте таблицу истинности для каждого элемента.
2. Используя полученные таблицы, дать алгебраическое описание рассмотренных элементов.
3. Для логических функций, записанных в табл.2
а) записать алгебраическое выражение логической функции;
б) преобразовать это выражение к логическому базису, включающему элемент И-НЕ;
в) реализовать логическую функцию на стенде и проверить результат.
Таблица
| Х1 | Х2 | Х3 | У1 | У2 | У3 | У4 | У5 | У6 | У7 |
4. Для логических функций, заданных алгебраически,
1)  ;
;
2)  ;
;
3)  ;
;
4)  :
:
а) составить таблицу;
б) упростить, используя основные аксиомы и теоремы;
в) составить схему;
г) реализовать схему на стенде и проверить результат.
5. Для логической функции, заданной табл.3.
Таблица 3
| Входы | Выходы | ||
| Х1 | Х2 | S | P |
Проделать то же, что и по п.3.
УКАЗАНИЕ ПО ОФОРМЛЕНИЮ ОТЧЕТА
Отчет оформляется каждым студентом и должен содержать подробное описание всех этапов выполнения работы с соответствующими схемами и таблицами.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие режимы работы транзисторов используется в элементах ТТЛ?
2. Можно ли на дискретных элементах реализовать, например, ТТЛ схему 2И-НЕ?
3. Какой вывод можно сделать, если сигнал на выходе ТТЛ схемы равен 1,5 В?
Лабораторная работа №6
Изучение основных элементов последовательной логики
(триггеры, регистры, и счетчики)
ВВЕДЕНИЕ
После того, как на предыдущих лабораторных работах изучены комбинационные схемы, т.е. схемы, в которых выходные сигналы в любой момент времени определяются только теми сигналами, которые поступают на вход системы в тот же момент времени, перейдем к изучению схем последовательной логики. Схема последовательной логики – это такая схема, в которой текущие значения выходов зависят не только от текущих значений входов, но и от работы схемы до текущего момента. Базовым элементом в последовательной логики является триггер. Триггер является основным компонентом более сложных последовательных устройств, таких, как счетчики, сдвиговые регистры и регистры памяти.
|
|
|
ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Триггер, или бистабильный мультивибратор, - одноразрядный элемент памяти, предназначенный для хранения логической переменной.
В общем случае структуры триггера можно представить следующей схемой:
 |
Х1 S
Q
Хn R
Q
С
Рис.1. Структура триггера
Переключение элемента памяти в то или иное состояние осуществляется сигналами S (set – установка), R (reset – сброс), поступающими с выходов схемы управления. Логическое значение сигналов S, R зависят от комбинации сигналов на внешних управляющих входа Х триггера и от состояния выхода элемента памяти, которое определяется значением сигнала Q, поступающего с выхода ЭП по цепи обратной связи.
Состояние триггера определяется значением выходного сигнала Q. Если изменение Q, т.е. переключение триггера, происходит только при поступлении синхроимпульса на специальный вход синхронизации С, то триггер называется синхронным. Триггеры могут синхронизироваться уровнем или фронтом синхроимпульсов (рис.2).
 С пф уи эф пф уи эф
С пф уи эф пф уи эф
t, c
t1 t2 t3 t4
Рис.2. Пример синхронизирующих сигналов
На рис.2 приняты следующие обозначения: ПФ – передний фронт импульса;
ЭФ – задний фронт импульса; УИ – уровень импульса; t1 и t3 – моменты появления импульса; t2 и t4 – моменты отсечки импульса.
Триггеры, синхронизируемые уровнем, могут изменять свое состояние в течении длительности синхроимпульса (например от момента t1 до момента t2 или от – t3 до t4) при поступлении соответствующих управляющих сигналов Х, т.е. могут переключаться несколько раз за время действия одного импульса. В течении паузы между синхроимпульсами состояние такого триггера сохраняется при любых изменениях управляющих сигналов. Триггеры, синхронизируемые фронтом, изменяют свое состояние при поступлении на синхронизирующий вход соответствующего фронта (переднего или заднего) синхроимпульса, т.е. в моменты времени t1, t2 или t3, t4, а при последующем действии уровня синхроимпульса это состояние сохраняется при любых изменениях управляющих сигналов Х. За время действия одного импульса такой триггер может переключаться только один раз.
|
|
|
Если триггер не имеет синхровхода, а имеет только управляющие входы, то такой триггер называется асинхронным. Переключение асинхронных триггеров происходит как только на управляющие входы поступает соответствующая комбинация управляющих сигналов Х.
В цифровой схемотехнике наиболее часто используются триггеры RS-, JK-, T- и D- типов. Буквами R и S, J и К, T и D принято обозначать управляющие входы Х триггеров соответствующих типов. Рассмотрим каждый из этих триггеров.
RS – триггеры
RS – триггер имеет два управляющих входа R и S, с помощью которых выполняются функции установки в состояние Q=1 (при S=1, R=0) и сброса в состояние Q=0 (при S=0, R=1). При S=R=0 триггер работает в режиме хранения, т.е. сохраняет ранее установленное состояние: либо Q=1, либо Q=0. Комбинация входных сигналов R=S=1 (установка и сброс одновременно) является запрещенной, так как может привести к неопределенному состоянию Q. Во избежание возникновения сбоев в цифровых системах комбинацию S=R=1 исключают. Таблицу состояний RS – триггера можно представить в следующем виде:
| R | S | Qn+1 |
| Qn Х |
Х – неопределенное состояние.
Условное обозначение RS – триггеров – ТР (например, 555ТР2).
RS – триггеры могут быть синхронными и асинхронными. Схемное изображение асинхронного RS – триггера показано на рис.3.
 |
R T Q
S ○ Q
Рис.3. асинхронный RS – триггер.
Работу асинхронного триггера можно пояснить временной диаграммой (рис.4).
 |
R
t
S
t
Q
t
Q
t
Рис.4 Временная диаграмма работы асинхронного RS – триггера
Синхронные триггеры могут быть синхронизируемыми уровнем или фронтом синхросигнала. Схемное изображение их показано на рис.5.
 |
R T R T
Q Q
C C
Q Q
S S
Рис.5. Условные обозначения синхронных RS – триггера, синхронизируемого уровнем.
Работу триггера, синхронизируемого уровнем, можно проиллюстрировать временной диаграммой (рис.6).
|
|
|
 |
R
t
S
t
C
t
Q
t
Q
t
Рис.6. Временная диаграмма работы синхронного RS – триггера,
синхронизируемого уровнем.
По аналогии, работу триггера, синхронизируемого, например, передним фронтом синхроимпульса, можно представить в виде рис.7.
 |
R
t
S
t
C
t
Q
t
Q
t
Рис.7. Временная диаграмма работы синхронного RS – триггера,
Синхронизируемого передним фронтом синхроимпульса.
JК – ТРИГГЕР
JК – триггер характеризуется следующей таблицей состояний:
| J | К | Qn+1 |
 0 0
| Qn Qn |
Он отличается от RS – триггера тем, что при поступлении на входы комбинации J=К=1 меняет состояние входа на противоположное
 |
Qn+1 = Qn.
Таким образом, JК – триггер не имеет запрещенных комбинаций входных сигналов. Так же как и RS – триггер, JК- триггер может быть как асинхронным, так и синхронизируемым уровнем или фронтом. Однако на практике обычно используются JК – триггеры, синхронизируемые фронтом. Условное обозначение JК – триггеров – ТВ (например, 155ТВ2), и условное графическое изображение дано на рис.8.
 |
J T
Q
C
 ○ Q
○ Q
K
Рис.8. Графическое изображение JК – триггеров
Т- ТРИГГЕР
Т – триггер называют часто счетным триггером, и он характеризуется следующей таблицей состояний:
| T | Qn+1 |

| Qn Qn |
 Состояние его выхода меняется на противоположное при поступлении на вход счетного сигнала Т=1 и сохраняется неизменным при Т=0. Из таблицы состояний для JК – триггера видно что при J=К=1 состояние JК – триггера, синхронизируемого фронтом, будет изменяться на противоположное
Состояние его выхода меняется на противоположное при поступлении на вход счетного сигнала Т=1 и сохраняется неизменным при Т=0. Из таблицы состояний для JК – триггера видно что при J=К=1 состояние JК – триггера, синхронизируемого фронтом, будет изменяться на противоположное
Qn+1=Qn
При поступлении каждого синхроимпульса. Таким образом, JК – триггер в этом случае функционирует как Т- триггер при подаче счетного сигнала Т на вход синхронизации С (рис.9).
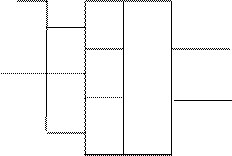 1 ○
1 ○
J Т
Q
Т ○ С
 ○ Q
○ Q
К
Рис.9. JК – триггер в режиме Т – триггера
D – ТРИГГЕР
D – триггер имеет таблицу состояний, в которой отсутствует состояние, соответствующее режиму хранения:
| D | Qn+1 |
D – триггеры бывают только асинхронными, и в соответствии с таблицей состояний, они после поступления синхросигнала устанавливаются в состояние Qn+1=D.
Таким образом, D – триггер выполняет функцию задержки информации, поступающей на управляющий вход D на один период синхросигнала.
В микроэлектронной аппаратуре широко используются как D – триггеры, синхронизируемые фронтом, так и синхронизируемые уровнем. Условное обозначение D – триггеров – ТМ (155ТМ2), а условное графическое изображение приведено на рис.10.
 |  |
D T Q D T Q
 |
 C ● C ○ Q
C ● C ○ Q
Q
Рис.10. Графическое изображение D – триггеров
Согласно таблицам состояний, синхронный JК – триггер будет выполнять функции D – триггера, если исключить комбинации переменных, при которых J=К.
Это получается соединением входов J и К через инвертор (рис.11).
 ○ J Т
○ J Т
D C Q
○ С
 ○ Q
○ Q
1 ○ К
Рис.11. JК – триггер в режиме D – триггера
В свою очередь, D – триггер, синхронизируемый фронтом, выполняет функции Т – триггера, если соединить вход D с инверсным выходом (рис.12).
 |
D T Q
T
 C
C
Q
Рис.12. D – триггер в режиме Т – триггера
Рассмотренные выше триггеры являются основным элементом, используемом при построении более сложных последовательных устройств, таких, как счетчики, регистры памяти, сдвиговые регистры и т.д.
Рассмотрим эти устройства.
СЧЕТЧИКИ
Счетчиком называется функциональный узел, на выводах которого образуется число, соответствующее количеству поступивших на вход импульсов. Основным параметром счетчика является модуль счета Кс. Модуль счета равен максимальному числу импульсов, которое может быть просчитано счетчиком. Счетчики строятся на основе JК -, Т- триггеров. Пример счетчика на D – триггерах показан на рис.13.
 |
D T D T D T
C ○ C ○ C ○
Вх 1 2 3
Рис.13. Счетчик на D – триггерах
Счетчик, содержащий m триггеров, называется m – разрядным.
Он может иметь 2 устойчивых состояния, поэтому его модуль счета Кс<2. Количество поступивших на счетный вход импульсов представляется на выходе счетчика в виде двоичного числа. Так, например, представленного выше трехразрядного счетчика можно проиллюстрировать временной диаграммой (рис.14).
Вх
 t
t
t
2 t
t
000 001 010 011 100 101 110 111 000 001 010 011
Рис.14. Временная диаграмма работы счетчика
Частота импульсов на выходе последнего разряда счетчика в Кс раз меньше, чем частота импульсов, поступающих на вход. Поэтому счетчики используются в качестве делителей частоты, обеспечивающих на выходе в Кс раз меньшую частоту сигнала, чем на входе.
По типу функционирования различают счетчики суммирующие, вычитающие и реверсивные. Суммирующий счетчик выполняет прямой счет, т.е. при поступлении на вход очередного импульса число на выход счетчика увеличивается на единицу. Вычитающий счетчик производит обратный счет, т.е. при поступлении счетного импульса число на выходе уменьшается на единицу. Реверсивный счетчик может работать в режиме прямого и обратного счета.
Если счетные импульсы в счетчике подаются только на вход триггера первого разряда, как в счетчике, представленном выше на рисунке, то такой счетчик называется последовательным.
Для каждого из последующих разрядов сигналы переключения поступают с выхода предыдущих разрядов. В результате происходит последовательное переключение разрядов счетчика.
Если период счетных импульсов соизмерим с временем задержки переключения одного разряда счетчика, то число на выходах последовательного счетчика может не всегда соответствовать количеству поступивших на вход импульсов. В этом случае наиболее подходящими являются параллельные счетчики. В счетчиках этого типа счетные импульсы одновременно (параллельно) поступают на синхровходы С триггеров во всех разрядах.
Условное обозначение счетчиков – ИЕ (например, 555 ИЕ 5),а условное графическое изображение дано на рис.15.
 а б
а б
D1 СТ2 /10
D2
S CT2 1 D4 1
2 D8 2
C 4 4
8 S 8
R
C 9
R
Рис.15. Графическое изображение счетчиков
На рис.15,а показан двоичный счетчик, а на рис.15,б двоично – десятичный с возможностью предварительной установки с помощью параллельного входа D1 – D8. Последний счетчик считается до 10, и далее цикл счета повторяется.
Регистры
Регистром называется функциональный узел, выполняющий хранение двоичных чисел, их сдвиг на определенное число разрядов. Они строятся на основе рассмотренных выше триггеров. По способу приема и выдачи информации регистры делятся на следующие группы: с параллельным приемом и выдачей (рис.16,а), с последовательным приемом и выдачей (рис.16,б), с последовательным приемом и параллельной выдачей (рис.16,б), с параллельным приемом и последовательной выдачей (рис.16,г), а также комбинированные с различными способами приема и выдачи.
 a Qm-1 Qm-2 Q1 Q0
a Qm-1 Qm-2 Q1 Q0
Tm-1 Tm-2... T1 To
Am-1 Am-2 A1 Ao
б
 Qo
Qo
Am-1..Ao
Tm-1 Tm-2 T1 To
C
 в
в
Qm-1 Qm-2 Q1 Qo
Am-1..Ao
 Tm-1 Tm-2 T1 To
Tm-1 Tm-2 T1 To
C
 г Qo
г Qo

Tm-1 Tm-2 T1 To
C
Am-1 Am-2 А1 Ао
Рис.16. Структурные схемы регистров
Регистры с параллельным приемом и выдачей информации используются для хранения информации и называются регистрами памяти. Изменение хранящейся информации, т.е. ввод иной информации происходит после соответствующего изменения сигналов на входах А при поступлении определенного уровня (0 или 1) или фронта синхросигналов С. для построения регистров памяти могут использоваться синхронизируемые уровнем или фронтом D – триггеры или RS – триггеры. В первом случае информация должна поступать в виде однофазных сигналов, а во втором виде парафазных сигналов. Примеры регистров памяти показаны на рис.17.
а б

 Ao
Ao
D T Qo Ao S T
Qo
 C C
C C
Qo ○ Qo
Ao R
A1
 D T Q1
D T Q1
A1 S T
 Q1
Q1
C Q1 C
○ Q1
A1 R
Am-1
D T Qm-1
 C
C
Qm-1 Am-1 S T
Qm-1
C
○ ○ Qm-1
C Am-1 R
C
Рис.17. Регистры памяти на D- и RS- триггерах
Регистры с последовательным приемом или последовательной выдачей информации называют часто сдвиговыми регистрами. В регистре с последовательным приемом и выдачей первый разряд вводимого числа Ао подается на вход одного старшего разряда регистра Тм – 1 и вводится в него
при поступлении первого синхроимпульса, т.е. Qm-1=Ao. При поступлении следующего синхроимпульса значение Ао, поступающее с выхода разряда Pm-1 вводится в разряд Tm-2, т.е. устанавливается Qm-2=Ao, а в разряд
Pm-1 поступает следующий разряд числа, т.е. Qm-1=A1 и т.д. Таким образом, производится последовательный сдвиг поступающей на вход информации на один разряд вправо в каждом такте синхросигналов. После поступления m синхроимпульсов весь регистр оказывается заполненным разрядами числа А, и первый разряд Ао появляется на выходе Qo регистра. В течение последующих m синхроимпульсов производится последовательный разрядный вывод из регистра записанного числа, после чего регистр оказывается полностью очищенным. Сдвиговые регистры обычно реализуются на D – триггерах (рис.18,а) или RS – триггерах (рис.18,б), где для ввода информации в первый разряд включается инвертор.
а
 A
A
D T D T D T Qo
C C C
C
б
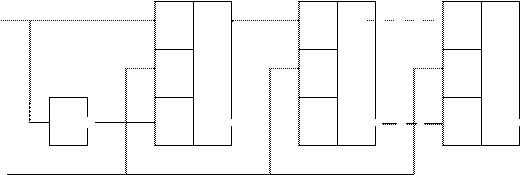 A
A
 S T S T S T Qo
S T S T S T Qo
C C C

 1 ○ R ○ R ○ R ○ Qo
1 ○ R ○ R ○ R ○ Qo
C
○
Рис.18. Сдвиговые регистры на D- и RS- триггерах
Для сдвиговых регистров обязательным является применение триггеров, синхронизируемых фронтом.
Сдвиговые регистры могут быть реверсивными, т.е. выполняющими сдвиг в любом направлении: слева направо или наоборот. Направление сдвига определяется значением управляющего сигнала на специальном входе регистра.
Условное обозначение регистров ИР (например, 155 ИР 1), и условное графическое изображение дано на рис.19.

D1 RG
D1
D3 1
D4 2
R 8
C
S
Рис.19. Графическое изображение четырехразрядного регистра
КРАТЕОЕ ОПИСАНИЕ ЛАБОРАТОРНОГО СТЕНДА УМ11
Для изучения работы триггеров, счетчиков и регистров используется лабораторный стенд УМ11. В верхней части стенда размещаются элементы комбинационной логики. Они имеют стандартные обозначения в виде прямоугольников синего цвета и пронумерованы от 1 до 31. Например, 15 – й по порядку элемент 4И – НЕ представлен на рис.20.
 |
&
○
Рис.20. Элемент 4И – НЕ
Эти элементы можно использовать при выполнении лабораторной работы в качестве вспомогательных логических элементов при построении сложных схем на основе триггеров.
В нижней части стенда расположены JK и D – триггеры. Они имеют на стенде стандартные обозначения в виде прямоугольников красного цвета и также пронумерованы по порядку от 1 до 12. Например, D – триггер 5 – й по порядку представлен на рис.21.
 |
R T Q
○
D
C Q
S Б
Рис.21. D – триггер
В самой нижней части стенда находятся 8 индикаторов и 8 тумблеров. Индикаторы используются при выполнении лабораторной работы для индикации логического уровня на выходе исследуемого логического элемента. Для этого необходимо выход логического элемента соединить с помощью специального коммутационного проводника с выходом одного из свободных индикаторов. Если на выходе элемента логическая “1”, то индикатор будет гореть, а если логический “0”, то индикатор погаснет. Вход индикатора имеет два равноценных гнезда, находящихся непосредственно над индикатором. С помощью индикаторов можно одновременно и независимо наблюдать за восемью логическими сигналами.
Тумблеры используются для задания требуемых логических сигналов при выполнении лабораторной работы. Каждый тумблер имеет два фиксированных положения и два выходных гнезда, расположенных над ним для съема логического сигнала. При верхнем положении тумблера верхнее гнездо дает логическую “1”, а нижнее – логический “0”. При нижнем положении тумблера все наоборот. Т.о. выходы каждого тумблера дают парафазный сигнал и всего можно задать восемь независимых парафазных сигналов.
В левом верхнем углу стенда имеется генератор синхроимпульсов, дающий парафазные сигналы фиксированной частоты 1 МГц и 500 кГц. Непосредственное использование этих синхроимпульсов в сочетании с индикаторами стенда не дает наглядной картины в силу высокой частоты синхроимпульсов. Например, если подать сигнал с генератора на индикатор, то индикатор будет просто тускло гореть. В этом случае необходимо привлекать дополнительную аппаратуру для наблюдения, например, осциллограф.
Если же использовать синхрогенератор в сочетании с генератором одиночных импульсов, который расположен на стенде ниже последнего, то можно получать одиночные синхроимпульсы в нужный момент времени, что позволит в статическом режиме наблюдать работу триггеров, регистров и счетчиков. Для этого необходимо на вход “синхр” генератора одиночных импульсов подать сигнал с генератора синхроимпульсов частоты 500 кГц или 1 МГц. Теперь при нажатии кнопки “ПУСК” на выходе генератора будет появляться один импульс. Для получения N импульсов необходимо на кнопку нажать N раз.
ЗАДАНИЕ НА РАБОТУ
Используя лабораторный стенд УМ11, изучить работу триггеров, счетчиков и регистров.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Изучение работы триггеров
а) Изучить работу RS – триггеров.
Для выполнения этой части работы необходимо, во – первых, собрать RS – триггер на элементах 2И – НЕ и снять для него таблицу истинности. Во – вторых, включая JK- и D- в режиме RS- триггера также снять таблицу истинности. Затем сравнить полученные результаты и сделать соответствующие выводы.
б) Изучить работу JK – триггера.
Собрать на стенде схему для исследования работы триггера и снять его таблицу истинности.
в) Изучить работу D – триггера.
Собрать на стенде схему для исследования работы триггера и снять его таблицу истинности.
2. Изучение работы счетчиков
Собрать на стенде трехразрядный суммирующий счетчик сначала на JK -, а затем на D- триггерах и зарисовать временные диаграммы его работы.
Затем собрать на стенде трехразрядный вычитающий счетчик на JK- и на
D- триггерах и зарисовать временные диаграммы его работы.
Используя дополнительные логические элементы собрать схему трехразрядного реверсивного счетчика.
3. Изучить работы регистров
Собрать схему регистра с параллельным вводом и параллельным выводом информации сначала на JK-, а затем на D- триггерах и показать его работоспособность.
Собрать схему регистра с последовательным вводом и последовательным выводом информации сначала на JK-, а затем на D- триггерах и показать его работоспособность.
Собрать схему кольцевого регистра.
|
|
|


