 |
Конструкция и расчет захватного устройства
|
|
|
|
При конструировании наиболее распространенных захватных устройств (ЗУ) роботов необходимо учитывать конкретный тип детали или группы деталей, их форму, материал и условия ТП. Важные критерии при этом – необходима точность удержания детали и допустимое усилие на губках. Исходя из этого разработано большое количество разных ЗУ, которые различаются кинематической схемой и другими конструктивными параметрами.
Усилие ЗУ должно соответствовать одному из значений ряда Ra10 в пределах 1 – 8000 Н: 1,0; 1,2; 1,6; 2,0; 2,5; 3,2; 4,0; 5,0; 6,3; 8,0; 10; 12; 16; 20; 25; 32; 40; 50; 63; 80; 100; 125; 160; 200; 250; 320; 400; 500; 630; 800; 1000; 1250; 1600; 2000; 2500; 3200; 4000; 5000; 6300; 8000.
Расчет ЗУ включает нахождение сил, которые действуют в местах контакта заготовки и губок; определение усилий привода; проверку отсутствия повреждений поверхности объекта при схвате; расчет на прочность деталей устройства.
 |
Рисунок 1.1 - Расчетная схема захвата
Усилие контактирования между деталью и губкой определяется по формуле
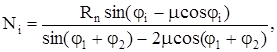(1.1)
где i, j = 1,2; i 
j,
Т.к. рассчитываемый захват симметричный, рассмотрим схему нагрузки одной из губок (см. рис. 1.2)
 |
Рисунок 1.2 - Схема нагрузки
Рабочие губки 4 соединены тягами с зубчатыми секторами 3, которые находятся в зацеплении с рейкой 2, связанной с тягой 1 привода. При перемещении рейки 2 под действием усилия F электромагнита происходит поворот губок 4 в направлении центра на одинаковые углы и охват объекта манипулирования.
Рассчитываем усилие контактирования между объектом и губкой. Пусть объект манипулирования будет в виде цилиндра массой m = 1кг.
Реакция на одну губку захвата.
(1.2)
где g – ускорение свободного падения.
|
|
|
Усиление контактирования между деталью и губкой определим по формуле (1.1).
При 
получим:
(1.3)
Коэффициент трения для пары фторопласт – керамика 0,2.
Усилие зажима на губке схвата равно:
(1.4)
Усилия, которые возникают в звеньях схвата при его работе, обозначены на рис. 1.2. Передаточный коэффициент механизма можно найти из условия:
(1.5)
Для определения этой зависимости составим условия равновесия системы относительно точки А (см. рис. 1.2).
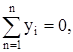(1.6)
т.е. сумма проекций всех сил на произвольно выбранные оси прямоугольных координат x,y и сумма моментов этих сил относительно точки А равняются нулю.
В нашем случае условия равновесия системы относительно точки А записуется в виде:
(1.7)
Решив систему относительно G и F получим уравнение:
, (1.8)
преобразовав которое получим:
или 
(1.9)
Задавшись соотношением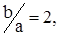 
коэффициентом запаса 
и коэффициентом полезного действия механизма 0,9, найдем:
(1.10)
Что мы проигрываем в рычажном механизме, в силе 
то мы выигрываем в расстоянии. Ход губок 20 мм, ход штока электромагнита 10мм.
Таким образом усилие электромагнита должно быть F=65H, а ход 
мм.
Для расчета электромагнита берем короткоходовую магнитную систему постоянного тока (Рис. 1.3).
Прямоходовые системы постоянного тока исполняются, как правило, в виде соленоидов. Поэтому такие системы часто называются соленоидными. В устарелых конструкциях соленоидные системы выполняются с открытым магнитопроводом.
Для удобства выбора формы электромагнита вводится понятие о конструктивном факторе (к. ф.), представляющим собой отношение
к.ф.= 
, (1.11)
где 
- сила электромагнита, кг;
- ход штока электромагнита, см.
Выбор формулы определяется на основании следующих соображений:
а) длина электромагнита пропорциональна требуемой величине хода - ;
б) поперечное сечение стали электромагнита определяется величиной требуемой начальной силы 
.
|
|
|
Каждой форме электромагнита соответствует определенная зона величины к.ф., при которых эта система выполняется с оптимальными данными по расходу материала.
Короткоходовые системы – предусматриваются для получения больших значений сил при относительно малом ходе якоря. Такие системы принимаются при больших значениях конструктивного фактора.
Исходными являются следующие данные:
начальная сила на якоре 
;
рабочий ход 
мм;
рабочее напряжение 
24В.
При проведении предварительного расчета не учитывают соленоидной силы, а принимают только силу притяжения якоря к стопу.
Некоторыми значениями параметров, определяющих собой габариты системы, приходится задаваться: индукцией 
в якоре рабочего зазора, падением магнитного потенциала в стали и в нерабочих зазорах - 
, температурой превышения катушки, отношением длины намотки катушки к толщине ее. Правильный выбор указанных параметров определяет экономичность конструкции.
 |
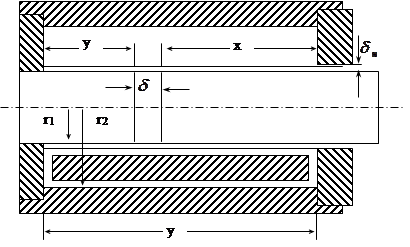Рисунок 1.3 Прямоходовая система с плоским стопом
Отношение длины катушки к толщине намотки.
Площадь сечения меди катушки 
принимают в зависимости от требуемого значения н.с. F. Значение 
может быть получено при разных отношениях 
.
При изменении этого отношения получают разные условия в отношении расхода меди и стали:
1) увеличение приводит к уменьшению расхода меди, так как при этом уменьшается объем меди и увеличивается поверхность охлаждения катушки;
2) уменьшение приводит к увеличению расхода стали, так как при этом увеличивается длина магнитопровода.
Минимальный вес всей конструкции достигается для различных видов электромагнитов и условий их работы разными путями.
Практикой установлено следующее: при относительно большом ходе якоря и малом значении силы принимаются большие значения , при увеличении силы и уменьшении хода – это отношение уменьшается.
Таким образом, и отношение можно фиксировать в функции значения к.ф. Значение колеблется в практически выполненных конструкциях в пределах 1 
8.
Значение 
выбирается в зависимости от конструктивного фактора и от режима работы катушки: чем больше значение к.ф., тем больше значение 
(см. Рис. 1.4)
|
|
|
Рисунок 1.4 - Кривые зависимости 
для магнитных систем: масштаб I – сплошные линии; масштаб II – пунктирные.
Короткоходовые системы предусматриваются для получения больших значений сил при относительно малом ходе якоря.
Рассчитаем коэффициент формы к.ф. для взятой короткоходовой системы:
(1.11)
Уравнение силы электромагнита имеет вид:
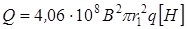(1.12)
Согласно графика рисунка 4 (масштаб 1) принимаем индуктивность в якоре
(1.13)
В рационально построенных конструкциях падение магнитного магнитного потенциала в стали магнитопровода составляется при начальном положении якоря 10-20% от величины н.с. катушки, а в нерабочих зазорах 5-10%
Следовательно
(1.14)
Индукция в стали кожуха
(1.15)
Нерабочий зазор 
определяется толщиной латунной направляющей трубки (порядка 0,5 мм) и зазор между трубкой и якорем. Этот зазор принимают порядка 0,125 мм для случая, когда внутренняя поверхность трубки не обработана, и 0,05 мм для трубки с обработанной внутренней поверхностью.
Отношение 
бывает в пределах 5 
8 и выбирается также в зависимости от значения к.ф. (график рис. 1.4). Толщина намотки 
принимается из условия 
, тогда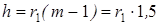 
Принимаем 
=0,7 тогда сила притяжения электромагнита будет равна
(1.12)
В процессе выполнения расчета короткоходовой системы мы получили силу притяжения электромагнита равной 70 Н.
Литература
1. Аш Ж., Андре П., Бофрон Ж. Датчики измерительных систем. В 2 т. Пер с фр. М.:Мир, 2002;
2. Бауман Э. Измерение сил электрическими методами: Пер. с нем. Мир, 1978. Энергоатомиздат, 2007;
3. Воротников С.А. Информационные устройства робототехнических систем. М.: Изд. МГТУ им. Н.Э.Баумана, 2005
4. Вульвет Дж. Датчики в цифровых системах: Пер. с англ. М.:Энергоиздат, 2001;
5. Гориневский Д.М. Формальский А.М., Шнейдер А.Ю. Управление манипуляционными системами на основе информации об усилиях. М.:Изд.фирма «Физико-математическая литература», 2004;
6. Погребной В.О., Рожанковский И.В., Юрченко Ю.П. Основы информационных процессов в роботизированном производстве;
|
|
|
7. Письменный Г.В., Солнцев В.И., Воротников С.А. Системы силомоментного очувствления роботов. М.: Машиностроение, 2000
8. Системы очувствления и адаптивные промышленные роботы. Под ред.Попова Е.П., Клюева В.В.;
9. Фу К., Гонсалес Р., Ли К. Робототехника. Пер. с англ.; Под ред В.Г. Градецкого. Мир, 2009.
|
|
|
