 |
Графическое решение квадратного уравнения
|
|
|
|
Введение
Необходимость решать квадратные уравнения еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения вавилоняне умели решать еще около 2000 лет до н.э. Правило решения этих уравнений, изложенное в Вавилонских текстах, совпадает по существу с современными, однако неизвестно, каким образом дошли вавилоняне до этого правила.
Формулы решения квадратных уравнений в Европе были впервые изложены в «Книге абака», написанной в 1202 году итальянским математиком Леонардо Фибоначчи. Его книга способствовала распространению алгебраических знаний не только в Италии, но и Германии, Франции и других странах Европы.
Но общее правило решения квадратных уравнений, при всевозможных комбинациях коэффициентов b и c было сформулировано в Европе лишь в 1544 году М. Штифелем.
В 1591 году Франсуа Виет ввел формулы для решения квадратных уравнений.
В древнем Вавилоне могли решить некоторые виды квадратных уравнений.
Диофант Александрийский и Евклид, Аль-Хорезми и Омар Хайям решали уравнения геометрическими и графическими способами.
В 7 классе мы изучали функции у = С, у = kx, у = kx + m, у = x 2, у = – x 2, в 8 классе – у = √ x, у = | x |, у = ax 2 + bx + c, у = k / x. В учебнике алгебры 9 класса я увидела ещё не известные мне функции: у = x 3, у = x 4, у = x 2n, у = x - 2n, у = 3√ x, (x – a) 2 + (у – b) 2 = r 2 и другие. Существуют правила построения графиков данных функций. Мне стало интересно, есть ли ещё функции, подчиняющиеся этим правилам.
Моя работа заключается в исследовании графиков функций и графическом решении уравнений.
|
|
|
Какие бывают функции
График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргументов, а ординаты – соответствующим значениям функции.
Линейная функция задаётся уравнением у = kx + b, где k и b – некоторые числа. Графиком этой функции является прямая.
Функция обратной пропорциональности у = k / x, где k ¹ 0. График этой функции называется гиперболой.
Функция (x – a)2 + (у – b)2 = r 2, где а, b и r – некоторые числа. Графиком этой функции является окружность радиуса r с центром в т. А (а, b).
Квадратичная функция y = ax 2 + bx + c где а, b, с – некоторые числа и а ¹ 0. Графиком этой функции является парабола.
Уравнение у 2(a – x) = x 2 (a + x). Графиком этого уравнения будет кривая, называемая строфоидой.
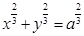Уравнение (x 2 + y 2)2 = a (x 2 – y 2). График этого уравнения называется лемнискатой Бернулли.
Уравнение. График этого уравнения называется астроидой.
Кривая (x2 y2 – 2 a x)2 =4 a2 (x2 + y2). Эта кривая называется кардиоидой.
Функции: у = x 3 – кубическая парабола, у = x 4, у = 1/ x 2.
Понятие уравнения, его графического решения
Уравнение – выражение, содержащее переменную.
Решить уравнение – это значит найти все его корни, или доказать, что их нет.
Корень уравнения – это число, при подстановке которого в уравнение получается верное числовое равенство.
Решение уравнений графическим способом позволяет найти точное или приближенное значение корней, позволяет найти количество корней уравнения.
При построении графиков и решении уравнений используются свойства функции, поэтому метод чаще называют функционально-графическим.
Для решения уравнение «делим» на две части, вводим две функции, строим их графики, находим координаты точек пересечения графиков. Абсциссы этих точек и есть корни уравнения.
Алгоритм построения графика функции
Зная график функции у = f (x), можно построить графики функций у = f (x + m), у = f (x)+ l и у = f (x + m)+ l. Все эти графики получаются из графика функции у = f (x) с помощью преобразования параллельного переноса: на │ m │ единиц масштаба вправо или влево вдоль оси x и на │ l │ единиц масштаба вверх или вниз вдоль оси y.
|
|
|
Графическое решение квадратного уравнения
На примере квадратичной функции мы рассмотрим графическое решение квадратного уравнения. Графиком квадратичной функции является парабола.
Что знали о параболе древние греки?
Современная математическая символика возникла в 16 веке.
У древнегреческих же математиков ни координатного метода, ни понятия функции не было. Тем не менее, свойства параболы были изучены ими подробно. Изобретательность античных математиков просто поражает воображение, – ведь они могли использовать только чертежи и словесные описания зависимостей.
Наиболее полно исследовал параболу, гиперболу и эллипс Аполоний Пергский, живший в 3 веке до н.э. Он же дал этим кривым названия и указал, каким условиям удовлетворяют точки, лежащие на той или иной кривой (ведь формул-то не было!).
Существует алгоритм построения параболы:
• Находим координаты вершины параболы А (х0; у0): х0 =- b /2 a;
• y0=ахо2+вх0+с;
• Находим ось симметрии параболы (прямая х=х0);
• Составляем таблицу значений для построения контрольных точек;
• Строим полученные точки и построим точки им симметричные относительно оси симметрии.
1. По алгоритму построим параболу y = x 2 – 2 x – 3. Абсциссы точек пересечения с осью x и есть корни квадратного уравнения x 2 – 2 x – 3 = 0.
Существует пять способов графического решения этого уравнения.
2. Разобьём уравнение на две функции: y = x 2 и y = 2 x + 3. Корни уравнения – абсциссы точек пересечения параболы с прямой.
3. Разобьём уравнение на две функции: y = x 2 –3 и y =2 x. Корни уравнения – абсциссы точек пересечения параболы с прямой.
4. Преобразуем уравнение x 2 – 2 x – 3 = 0 при помощи выделения полного квадрата на функции: y = (x –1)2 и y =4. Корни уравнения – абсциссы точек пересечения параболы с прямой.
5. Разделим почленно обе части уравнения x 2 – 2 x – 3 = 0 на x, получим x – 2 – 3/ x = 0, разобьём данное уравнение на две функции: y = x – 2, y = 3/ x. Корни уравнения – абсциссы точек пересечения прямой и гиперболы.
|
|
|
|
|
|
