Главная | Обратная связь | Поможем написать вашу работу!

Свойства от синусоидальной спирали

Спирали

Спирали (франц., единственное число spirale, от лат. spira, греч. speira — виток), плоские кривые линии, бесчисленное множество раз обходящие некоторую точку, с каждым обходом приближаясь к ней или с каждым обходом удаляясь от неё.

Если выбрать точку за полюс полярной системы координат, то полярное уравнение спирали

r = f (j) таково, что f (j + 2p) > f (j) или f (j + 2p) < f (j) при всех j. В частности, спирали получаются, если f (j) — монотонно возрастающая или убывающая положительная функция.

Наиболее простой вид имеет уравнение архимедовой спирали: r = а j, изученной древнегреческим математиком Архимедом (3 в. до н. э.) в связи с задачами трисекции угла и квадратуры круга в сочинении "О спиралях".

Из других спиралей практическое значение имеет спираль Корню (или клотоида), применяемая при графическом решении некоторых задач дифракции. Параметрическое уравнение этой С. имеет вид:

Спираль Корню является идеальной переходной кривой для закругления железнодорожного пути, так как её радиус кривизны возрастает пропорционально длине дуги. Спиралями являются также эвольвенты замкнутых кривых, например эвольвента окружности.

Названия некоторым спиралям даны по сходству их полярных уравнений с уравнениями кривых в декартовых координатах, например:

· параболическая спираль (а - r)² = b j,

· гиперболическая спираль: r = а /j.

· Жезл: r² = a/j

· si-ci-cпираль, параметрические уравнения которой имеют вид:

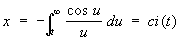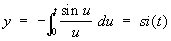
[si (t) и ci (t) —интегральный синус и интегральный косинус]. Кривизна si-ci-cпирали изменяется с длиной дуги по закону показательной функции. Такие спирали применяют в качестве профиля для лекал.

Напоминает спираль кривая 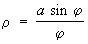, называемая кохлеоидой. Она бесконечное множество раз проходит через полюс, причём каждый следующий завиток лежит в предыдущем.

Спирали встречаются также при рассмотрении особых точек в теории дифференциальных уравнений

Спиралями иногда называют также пространственные кривые, делающие бесконечно много оборотов вокруг некоторой оси, например винтовая линия.

Кардиоиды

Кардиоида (греч. καρδία — сердце, греч. εἶδος — вид) — плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом. Получила своё название из-за схожести своих очертаний со стилизованным изображением сердца.

Кардиоида является частным случаем улитки Паскаля, эпициклоиды и синусоидальной спирали.

Так же можно сказать, что Кардиоида-это плоская кривая, описываемая точкой М окружности, которая извне касается неподвижной окружности того же радиуса и катится по ней без скольжения. Принадлежит к эпициклоидам (плоская кривая, описываемая точкой окружности, которая извне касается неподвижной окружности и катится по ней без скольжения, к ним относятся кардиоиды, циклоиды, гипоциклоиды). Является алгебраической кривой второго порядка.

Уравнения кардиоиды:

· В прямоугольной системе координат:

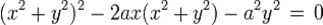
· В прямоугольной системе координат (параметрическая запись):

x = 2 r cos t (1 + cos t)

y = 2 r sin t (1 + cos t)

· В полярной системе координат:

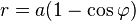
· Длина дуги одного витка кардиоиды, заданной формулой:

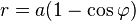
равна:

s = 8 a.

· Площадь фигуры, ограниченной кардиоидой, заданной формулой:

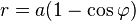равна: .

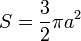Свойства кардиоиды:

1. Касательная в произвольной точке кардиоиды проходит через точку окружности производящего круга, диаметрально противоположной точке касания кругов, а нормаль — через точку их касания.2. Угол, составляемый касательной к кардиоиде с радиус-вектором точки касания, равен половине угла, образуемого этим радиус-вектором с полярной осью.3. Касательные к кардиоиде, проведенные в концах хорды, проходящей через полюс, взаимно перпендикулярны. Циклоиды

Циклоида (от греч. κυκλοειδής — кругообразный) — плоская трансцендентная кривая. Циклоида определяется кинематически как траектория фиксированной точки производящей окружности радиуса r, катящейся без скольжения по прямой.

Свойства:

1. Циклоида — периодическая функция по оси абсцисс, с периодом 2π r. За границы периода удобно принять особые точки (точки возврата) вида t = 2π k, где k — произвольное целое число.

2. Для проведения касательной к циклоиде в произвольной её точке A достаточно соединить эту точку с верхней точкой производящей окружности. Соединив A с нижней точкой производящей окружности, мы получим нормаль.

3. Длина арки циклоиды равна 8 r. Это свойство открыл Кристофер Рен (1658).

4. Площадь под каждой аркой циклоиды втрое больше, чем площадь порождающего круга. Торричелли сообщил, что этот факт Галилей открыл экспериментально: сравнил вес пластинок с кругом и с аркой циклоиды.

5. Радиус кривизны у первой арки циклоиды равен .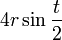

6. «Перевёрнутая» циклоида является кривой скорейшего спуска (брахистохроной). Более того, она имеет также свойство таутохронности: тяжёлое тело, помещённое в любую точку арки циклоиды, достигает горизонтали за одно и то же время.

7. Период колебаний материальной точки, скользящей по перевёрнутой циклоиде, не зависит от амплитуды, этот факт был использован Гюйгенсом для создания точных механических часов.

8. Эволюта циклоиды является циклоидой, конгруэнтной исходной, а именно — параллельно сдвинутой так, что вершины переходят в «острия».

9. Детали машин, которые совершают одновременно равномерное вращательное и поступательное движение, описывают циклоидальные кривые (циклоида, эпициклоида, гипоциклоида, трохоида, астроида) (ср. построение лемнискаты Бернулли).

Уравнения

Примем горизонтальную ось координат в качестве прямой, по которой катится производящая окружность радиуса r.

· Циклоида описывается параметрически:

x = rt − r sin t,

y = r − r cos t.

· Уравнение в декартовой прямоугольной системе координат:

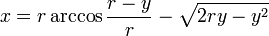
Циклоида может быть получена как решение дифференциального уравнения:

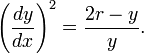
Астроида

Астроида — плоская кривая, описываемая точкой M окружности радиуса r, катящейся по внутренней стороне окружности радиуса R = 4 r. Иначе говоря, астроида — это гипоциклоида с модулем m = 4.

Так же можно сказать, что Астроида- это плоская кривая, описываемая точкой окружности, которая касается изнутри неподвижной окружности вчетверо большего радиуса и катится по ней без скольжения. Принадлежит к гипоциклоидам. Является алгебраической кривой шестого порядка.

Свойства

1. Имеются четыре каспа.

2. Длина дуги от точки с 0 до

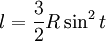
4. Длина всей кривой 6 R.

5. Радиус кривизны:

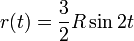
7. Площадь, ограниченная кривой:

9. Астроида является огибающей семейства отрезков постоянной длины, концы которых расположены на двух взаимно перпендикулярных прямых.

10. Астроида является алгебраической кривой 6-го порядка.

Уравнения

· Уравнение в декартовой прямоугольной системе координат:

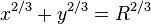
· параметрическое уравнение:

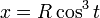
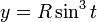
Лемниската Бернулли

Лемниската Бернулли — плоская кривая, геометрическое место точек, произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату половины расстояния между фокусами.

Так же можно сказать, что Лемниската Бернулли- это плоская кривая, имеющая вид «восьмерки»; множество точек М, произведение расстояний r1 и r2 которых до двух данных точек F1 и F2 (фокусов) равно квадрату междуфокусного расстояния. Алгебраическая кривая 4-го порядка, рассмотренная Я. Бернулли (1964 г).

Уравнения

Рассмотрим простейший случай: если расстояние между фокусами 2 c, расположены они на оси OX, и начало координат делит отрезок между ними пополам, то следующие уравнения задают лемнискату:

· в прямоугольной декартовой системе координат:

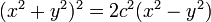
Фокусы лемнискаты — F ₁(− c;0) и F ₂(c;0). Возьмём произвольную точку M (x; y). Произведение расстояний от фокусов до точки M есть

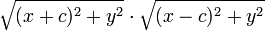и по определению оно равно c ²:

Возводим в квадрат обе части равенства:

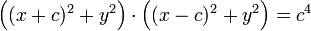
Раскрываем скобки в левой части:

Раскрываем скобки и свёртываем новый квадрат суммы:

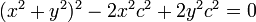
Выносим общий множитель и переносим:

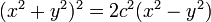
Далее можно сделать замену a ² = 2 c ², хотя это не обязательно:

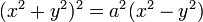
В данном случае a — радиус окружности, описывающей лемнискату.

Проведя несложные преобразования, можно получить явное уравнение:

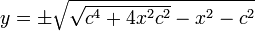
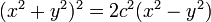
Возводим в квадрат и раскрываем скобки:

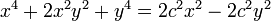
Приводим к виду

Это квадратное уравнение относительно y ². Решив его, получим

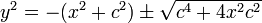
Взяв корень и отбросив вариант с отрицательным вторым слагаемым, получим:

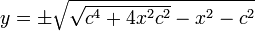
где положительный вариант определяет верхнюю половину лемнискаты, отрицательный — нижнюю.

·в полярной системе координат:

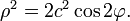
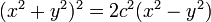
Используя формулы перехода к полярной системе координат 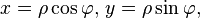получим:

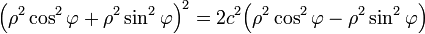
Выносим общие множители и используем тригонометрическое тождество sin²α + cos²α = 1:

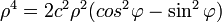
Используем ещё одно тождество: cos²α − sin²α = cos 2α:

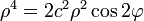
Делим на ρ², предполагая, что :

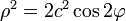Как и в случае прямоугольной системы можно заменить a ² = 2 c ²:

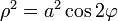
Плотность точек кривой при равномерном изменении параметра

· Параметрическое уравнение в прямоугольной системе:

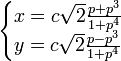, где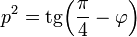

Это единственный вариант рациональной параметризации кривой. Уравнение полностью описывает кривую, когда параметр пробегает всю вещественную прямую: от 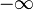до 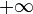. При этом, когда параметр стремится к 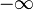, точка кривой стремится к (0;0) из второй координатной четверти, а когда параметр стремится к , то — из четвёртой. Распределение точек, которые даёт параметрическое уравнение, при изменении его параметра с фиксированным шагом показано на рисунке.

Свойства

Лемниската Бернулли является частным случаем овала Кассини при a = c, синусоидальной спирали с индексом n = 2 и лемнискаты Бута при c = 0, поэтому она наследует некоторые свойства этих кривых.

Свойства от овала Кассини

· Лемниската — кривая четвёртого порядка.

· Она симметрична относительно двойной точки — середины отрезка между фокусами.

· Кривая имеет 2 максимума и 2 минимума. Их координаты:

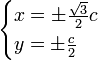
· Расстояние от максимума до минимума, находящихся по одну сторону от серединного перпендикуляра отрезка между фокусами равно расстоянию от максимума (или от минимума) до двойной точки.

· Лемнискату описывает окружность радиуса 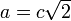, поэтому иногда в уравнениях производят эту замену.

Свойства от синусоидальной спирали

· Точка, где лемниската пересекает саму себя, называется узловой или двойной точкой.

· Касательные в двойной точке составляют с отрезком F ₁ F ₂ углы .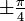

· Угол μ, составляемый касательной в произвольной точке кривой с радиус-вектором точки касания равен .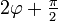

· Касательные в точках пересечения кривой и хорды, проходящей через двойную точку, параллельны друг другу.

· Инверсия относительно окружности с центром в двойной точке, переводит лемнискату Бернулли в равнобочную гиперболу.

· Радиус кривизны лемнискаты есть

Есть частный случай формулы радиуса кривизны синусоидальной спирали:

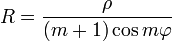при m = 2,

однако, легко вывести и по определению.

Уравнение лемнискаты в полярной системе:

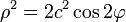
Формулы перехода к полярной системе координат:

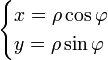
Выражаем :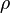

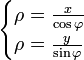
Подставляем в уравнение лемнискаты и выражаем x и y:

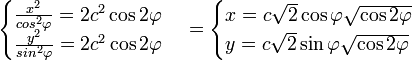
—- это параметрическое уравнение относительно 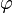. Проведя некоторые тригонометрические преобразования, можно получить уравнение относительно 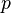, указанное выше в разделе Уравнения.

Формула радиуса кривизны кривой, заданной параметрически:

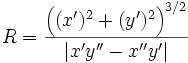
Находим производные по :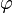

Подставляем в формулу радиуса:

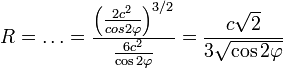
Возвращаемся к уравнению лемнискаты:

Подставляем это выражение в полученную формулу радиуса и получаем:

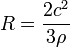
·Натуральное уравнение кривой имеет вид

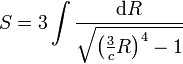
· Подерой лемнискаты является синусоидальная спираль

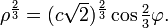
· Лемниската сама является подерой равносторонней гиперболы.

Собственные свойства:

Гравитационное свойство лемнискаты

· Кривая является геометрическим местом точек, симметричных с центром равносторонней гиперболы относительно её касательных.

· Отрезок биссектрисы угла между фокальными радиус-векторами точки лемнискаты равен отрезку от центра лемнискаты до пересечения её оси с этой биссектрисой.

· Материальная точка, движущаяся по кривой под действием однородного гравитационного поля, пробегает дугу за то же время, что и соответствующую хорду. При этом ось лемнискаты составляет угол 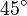с вектором напряжённости поля, а центр лемнискаты совпадает с исходным положением движущейся точки.

· Площадь полярного сектора 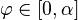, при :

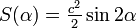
o В частности, площадь каждой петли 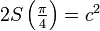, то есть площадь, ограниченная кривой, равна площади квадрата со стороной .

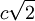· Перпендикуляр, опущенный из фокуса лемнискаты на радиус-вектор какой-либо её точки, делит площадь соответствующего сектора пополам.

· Длина дуги лемнискаты между точкам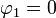и и 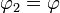выражается эллиптическим интегралом рода:

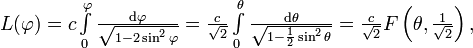где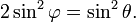

o В частности, длина всей лемнискаты

Приложение

В геометрии, синусоидальная спираль — семейство кривых, определяемое уравнением в полярной системе координат:

rⁿ = aⁿ cos(n θ),

где a — ненулевая константа и n — рациональное число, не равное нулю. С учетом возможности поворота кривой относительно начала координат уравнение также может быть записано в виде:

rⁿ = aⁿ sin(n θ)

Использование термина «спираль» в данном случае не является точным, т. к. получаемые кривые по форме скорее напоминают цветок. Многие известные кривые являются частными случаями синусоидальной спирали:

· Прямая (n = −1)

· Окружность (n = 1)

· Гипербола (n = −2)

· Парабола (n = −1/2)

· Кардиоида (n = 1/2)

· Лемниската Бернулли (n = 2)

Впервые была изучена Маклореном.

Воспользуйтесь поиском по сайту: