При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.

35.

Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.

1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:

Пример. Число перевести в десятичную систему счисления.

2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:

Пример. Число 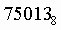перевести в десятичную систему счисления.

3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:

Пример. Число перевести в десятичную систему счисления.

Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.

Пример. Число перевести в двоичную систему счисления.

Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.

Пример. Число 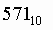перевести в восьмеричную систему счисления.

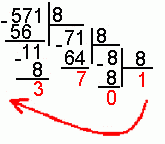
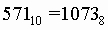
Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.

Пример. Число перевести в шестнадцатеричную систему счисления.

7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).

Пример. Число перевести в восьмеричную систему счисления.

8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).

Пример. Число перевести в шестнадцатеричную систему счисления.

Для перевода восьмеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой.

Пример. Число перевести в двоичную систему счисления.

Для перевода шестнадцатеричного числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.

Пример. Число перевести в двоичную систему счисления.

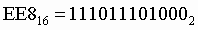
При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.

Пример 1. Число перевести в восьмеричную систему счисления.

Пример 2. Число перевести в шестнадцатеричную систему счисления.

65 оперативная память. Из нее процессор берет программы и исходные данные для обработки, в нее он записывает полученные результаты. Название «оперативная» эта память получила потому, что она работает очень быстро, так что процессору практически не приходится ждать при чтении данных из памяти или записи в память. Однако содержащиеся в ней данные сохраняются только пока компьютер включен.

Кэш-память. Для ускорения доступа к оперативной памяти на быстродействующих компьютерах используется специальная кэш-память, которая располагается как бы «между микропроцессором и оперативной памятью и хранит копии наиболее часто используемых участков оперативной памяти.

ВIOS (постоянная память). В компьютере имеется также и постоянная память, в которую данные занесены при изготовлении. Как правило, эти данные не могут быть изменены, выполняемые на компьютере программы могут только их считывать.

CMOS (полупостоянная память). Кроме обычной оперативной памяти и постоянной памяти, в компьютере имеется также небольшой участок памяти для хранения параметров конфигурации компьютера. Его часто называют CMOS -памятью, поскольку эта память обычно выполняется по технологии, обладающей низким энергопотреблением. Содержимое CMOS -памяти не изменяется при выключении энергопитания компьютера, поскольку для ее электропитания используется специальный аккумулятор.

Видеопамять. Еще один вид памяти в компьютерах это видеопамять, то есть память, используемая для хранения изображения, выводимого на экран монитора. Эта память обычно входит в состав видеоконтроллера - электронной схемы, управляющей выводом изображения на экран.

 

66 Контроль четности означает, что при записи байта информации в запоминающее устройство определяется дополнительный контрольный бит, в который записывается 0, если это число — четное, и 1 — если оно нечетное. Таким образом, при чтении ранее записанного байта, вновь получив контрольный бит и сравнив его с уже имеющимся, можно говорить о достоверности получаемой информации. Такая операция особенно актуальна для запоминающих устройств невысокой надежности, в частности, для дисковых накопителей. Современные технологические успехи в области полупроводниковой памяти позволяют в ряде случаев обходиться без контроля четности. Некоторые материнские платы хотя и допускают использование модулей памяти с контролем четности, но саму проверку могут не поддерживать.

В ответственных приложениях, требующих повышенной надежности хранения информации, применяются более серьезные, чем контроль четности, методы обеспечения целостности данных. К ним относятся корректирующие коды (ECC — Error Correction Code), позволяющие не только обнаруживать ошибки, но и восстанавливать искаженную информацию за счет ее избыточности. Так, существуют модули памяти со схемами ECC, в которых для хранения контрольной информации используются не один, а два бита, в которых хранится остаток от деления числа на 4. Благодаря этим данным схема ECC умеет обнаруживать и исправлять одиночные искаженные биты, а также обнаруживать (но не исправлять) двойные ошибки. Модули памяти с ECC обычно стоят заметно дороже и применяются в основном в серверах.

В общем случае ECC применяются во всех современных дисковых и ленточных накопителях. За счет информационной избыточности закодированных данных удается восстанавливать поврежденные блоки информации длиной в сотни байт. Наиболее широко применяются помехоустойчивые коды Рида-Соломона (Reed-Solomon). Например, благодаря использованию этих кодов в стримере на базе бытового видеомагнитофона «АрВид» удается годами хранить информацию на обычных видеокассетах VHS без потери данных, несмотря на очень низкую надежность физического носителя информации. Коды Рида-Соломона применяются и в жестких дисках.

Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.

Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение. Сегодня, я опишу самый простой алгоритм Хемминга, который может исправлять лишь одну ошибку.

Также стоит отметить, что существуют более совершенные модификации данного алгоритма, которые позволяют обнаруживать (и если возможно исправлять) большее количество ошибок.

Сразу стоит сказать, что Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.

50 Синтез вычислительных схемсводится к Трем этапам:

1.Образование СДНФ функции по заданной таблице истинности.

Таблица истинности- табличное представление вычислительной схемы.

2.Упрощение этой функции(преобразование СДНФ в формулу с наименьшим числом вхождений переменных).

3.Построение соответствующей схемы.

1.Образование СДНФ функции по заданной таблице истинности:

1.В таблице выделяются наборы значений аргументов, при которых функция принимает единичное значение.

2.для каждого выделенного набора образуется конституэнта единицы, принимающая единичное значение при данном наборе значений аргумента.

3.составляется логическая сумма образованных конституэнт единицы.

При составления совершенной конъюнктивной нормальной формы функции:

1.в таблице выделяются наборы значений аргументов, при которых функция принимает нолевое значение.

2.для каждого выделенного набора образуется конституэнта ноля, принимавшая нолевое значение при данном наборе значений аргументов.

3.составляется логическое произведение образованнх конституэнт ноля.

2. Упрощение этой функции. При преобразование СДНФ в формулу с наименьшим числом вхождений переменных(минимизация формулы) используются следующие основные приемы:

-вынос за скобки

-полное склеивание

-поглощение

-Минимизация по методу Квайна

-минимизация с использование карт Карто или диаграмм Вейча

При минимизации по методу Квайна предполагается,что исходная функция задана в СДНФ. Конъюнкция, получаемая в результате склеивания двух конституэнт единицы, называется импликантой. Импликанта поглащает конституэнты единицы, при склеивании которых она образовалась.

Диаграмма Вейча или карта Карто - таблица, облегчающая нахождение склеивающихся конституэнт единицы и получение набора простых импликант.

Задача минимизации по методу Квайна:

1. В СДНФ функции выполняются всевозможные склеивания конституэнт единицы и получаемых импликант, и выделяются все простые импликанты.

2. Из набора простых импликант выделяется наименьший по числу импликант поднабора простых импликант, поглащающих в совокупности наибольшее число конституэнт единицы

3.Образовывается логическая сумма простых импликант, вошедших в выделенный поднабор, и конституэнт единиц, не учавствующих в склеивании.

3.Построение схемы. В качестве примера логического синтеза вычислительных схем выделим построение одноразрядного двоичного сумматора, имеющего два выхода и два входа

 

Поделиться:

Воспользуйтесь поиском по сайту: