 |
Расчет вероятности безотказной работы системы
|
|
|
|
Предмет: «Надежность, эргономика и качество АСОИУ»
Расчетное задание
Вариант 39
Студент: Девяткин Е. А.
Группа: АС-05-1
Преподаватель: Прохоров В. С.
Новомосковск 2009 г.
Задание
По структурной схеме надежности технической системы в соответствии с вариантом задания, требуемому значению вероятности безотказной работы системы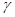 
и значениям интенсивностей отказов ее элементов 
требуется:
1. Построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0.1 - 0.2.
2. Определить 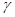- процентную наработку технической системы.
3. Обеспечить увеличение 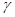- процентной наработки не менее, чем в 1.5 раза за счет:
а) повышения надежности элементов;
б) структурного резервирования элементов системы.
Все элементы системы работают в режиме нормальной эксплуатации (простейший поток отказов). Резервирование отдельных элементов или групп элементов осуществляется идентичными по надежности резервными элементами или группами элементов. Переключатели при резервировании считаются идеальными.
На схемах обведенные пунктиром m элементов являются функционально необходимыми из n параллельных ветвей.
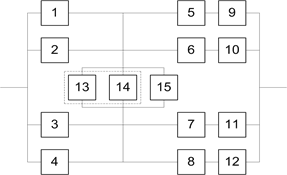
| № | , | Интенсивности отказов элементов, , x10-6 1/ч | ||||||||||||||
| вар. | % | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 39 | 90 | 8.0 | 3.0 | 5.0 | 2.0 | |||||||||||
Расчетная часть
Расчет начинаем с упрощения исходной схемы.
Элементы 1-2 и 3-4 соединены параллельно. Заменяем 1-2 на элемент A, а 3-4 на элемент B.
Рисунок 2.1 – Преобразованная схема
По условию, интенсивности отказов элементов 1-4 равны. Следовательно, вероятность безотказной работы каждой пары элементов одинакова.
|
|
|
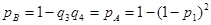
Элементы 5-9, 6-10, 7-11, 8-12 соединены последовательно. Заменяем их на элементы C, D, E и F.
Рисунок 2.2 – Преобразованная схема
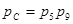
Интенсивности отказов элементов 5-8 и 9-12 соответственно равны. Значит, что для каждого из этих последовательных соединений вероятность безотказной работы одинакова:
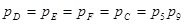
Элементы C-D, E-F соединены параллельно. Заменяем их элементами G и H.
Рисунок 2.3 – Преобразованная схема
Вероятность их безотказной работы одинакова и равна:
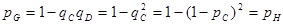
Заменяем оставшиеся элементы 13, 14 и 15 на элемент I:
Рисунок 2.4 – Преобразованная схема
Элементы 13,14 и 15 образуют соединение «2 из 3». Интенсивность отказов этих элементов равна. Следовательно, для определения вероятности безотказной работы можно воспользоваться комбинаторным методом:
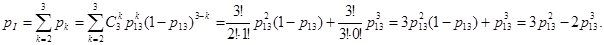
Элементы A, B, G, H и I образуют мостиковую схему (рис. 2.4). Вероятность ее безотказной работы определяется по теореме разложения:
Учитывая, что pA=pB и pG=pH, получаем:
Согласно расчетам в Microsoft Excel и исходным данным наименее надежными элементами являются 1-4 и 9-12.
Наработку необходимо увеличить с γ=0,07973805*106 ч. до 0,119607075*106 ч.
Повышение надежности системы можно провести двумя способами:
1) Заменой малонадежных элементов на более надежные.
2) Структурным резервированием элементов.
Первый способ
Заменяем элементы 1-4, имеющие λ=8*10-6 1/ч, на элементы с λ=4*10-6 1/ч; элементы 9-12 с λ=5*10-6 1/ч на элементы с λ=3*10-6 1/ч. Новые значения рассчитаны в Excel.
При этом вероятность безотказной работы системы вырастет с 0,7199967 до 0,9061834.
Второй способ
Используем постоянно включенный резерв. Подключаем параллельно дополнительные элементы:
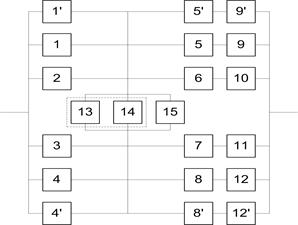
Рисунок 2.5 – Система с резервированием
При этом увеличивается вероятность безотказной работы каждого из квазиэлементов A, B, G и H. Новые значения рассчитаны в Excel.
|
|
|
При этом вероятность безотказной работы системы вырастет с 0,7199967 до 0,9235133.
Расчет вероятности безотказной работы системы
|
|
|
|
|
|
|
|
|
|
|
|
| |
| Элемент | i | Наработка t, x 106 ч | ||||||||||
| x10-6 ч-1 | 0,01 | 0,045 | 0,08 | 0,115 | 0,15 | 0,185 | 0,22 | 0,255 | 0,0797381 | 0,1196071 | ||
| Исходная система | ||||||||||||
| 1, 2, 3, 4 | 8 | 0,9231163 | 0,6976763 | 0,5272924 | 0,398519 | 0,3011942 | 0,2276377 | 0,1720449 | 0,1300287 | 0,5283986 | 0,3840984 | |
| 5, 6, 7, 8 | 3 | 0,9704455 | 0,8737159 | 0,7866279 | 0,7082204 | 0,6376282 | 0,5740723 | 0,5168513 | 0,4653339 | 0,7872463 | 0,6984992 | |
| 9, 10, 11, 12 | 5 | 0,9512294 | 0,7985162 | 0,67032 | 0,5627049 | 0,4723666 | 0,3965314 | 0,3328711 | 0,279431 | 0,6711986 | 0,5498909 | |
| 13, 14, 15 | 2 | 0,9801987 | 0,9139312 | 0,8521438 | 0,7945336 | 0,7408182 | 0,6907343 | 0,6440364 | 0,6004956 | 0,8525903 | 0,7872463 | |
| A, B | - | 0,9940889 | 0,9086004 | 0,7765476 | 0,6382207 | 0,5116705 | 0,4034565 | 0,3144903 | 0,24315 | 0,7775921 | 0,6206652 | |
| C, D, E, F | - | 0,9231163 | 0,6976763 | 0,5272924 | 0,398519 | 0,3011942 | 0,2276377 | 0,1720449 | 0,1300287 | 0,5283986 | 0,3840984 | |
| G, H | - | 0,9940889 | 0,9086004 | 0,7765476 | 0,6382207 | 0,5116705 | 0,4034565 | 0,3144903 | 0,24315 | 0,7775921 | 0,6206652 | |
| I | - | 0,9988393 | 0,9790516 | 0,9408803 | 0,8906988 | 0,8332956 | 0,7722238 | 0,7100781 | 0,6487135 | 0,9412175 | 0,8834678 | |
| P | 0,99993 | 0,9830731 | 0,899071 | 0,7437079 | 0,5591191 | 0,3885224 | 0,2540314 | 0,1586875 | 0,9 | 0,7199967 | ||
| Повышение надежности заменой малонадежных элементов | ||||||||||||
| (1, 2, 3, 4)' | 4 | 0,9607894 | 0,8352702 | 0,726149 | 0,6312836 | 0,5488116 | 0,4771139 | 0,4147829 | 0,3605949 | 0,7269103 | 0,6197567 | |
| (9, 10, 11, 12)' | 3 | 0,9704455 | 0,8737159 | 0,7866279 | 0,7082204 | 0,6376282 | 0,5740723 | 0,5168513 | 0,4653339 | 0,7872463 | 0,6984992 | |
| (A, B)' | - | 0,9984625 | 0,9728641 | 0,9250057 | 0,8640483 | 0,7964291 | 0,7265901 | 0,657521 | 0,5911612 | 0,925422 | 0,855415 | |
| (C, D, E, F)' | - | 0,9417645 | 0,7633795 | 0,6187834 | 0,5015761 | 0,4065697 | 0,329559 | 0,2671353 | 0,2165357 | 0,6197567 | 0,4879012 | |
| (G, H)' | - | 0,9966086 | 0,9440107 | 0,8546739 | 0,7515736 | 0,6478404 | 0,5505088 | 0,4629093 | 0,3861836 | 0,855415 | 0,7377548 | |
| P' | 0,9999861 | 0,9960727 | 0,9723562 | 0,9161476 | 0,8273495 | 0,7159142 | 0,5956128 | 0,4788057 | 0,9726461 | 0,9061834 | ||
| Повышение надежности с помощью резервирования элементов | ||||||||||||
| (A, B)'' | - | 0,9995455 | 0,9723677 | 0,8943723 | 0,7823966 | 0,6587525 | 0,5392523 | 0,4324287 | 0,3415622 | 0,8951121 | 0,7663671 | |
| (G, H)'' | - | 0,9998025 | 0,9867518 | 0,9445993 | 0,8761783 | 0,7910178 | 0,6986427 | 0,6063852 | 0,5190968 | 0,9450225 | 0,8657045 | |
| P'' | 0,9999998 | 0,9990464 | 0,9852233 | 0,9340052 | 0,8325726 | 0,6923442 | 0,5388721 | 0,3960116 | 0,9854358 | 0,9235133 | ||
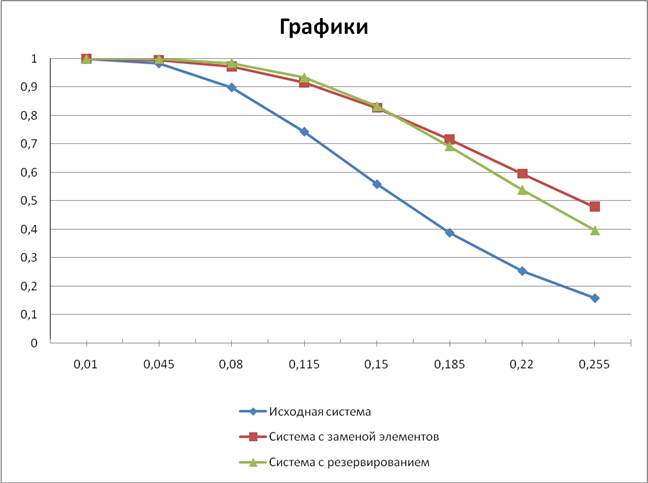
Рисунок 2.6 – Графики
Вывод: по полученным графикам видно, что замена элементов более эффективна для повышения надежности, если систему планируется использовать в течение продолжительного времени. Если же критичным является надежная работа системы в первое время, то резервирование предпочтительней. Но разница не столь значительна, как в первом случае.
|
|
|
|
|
|
