Лекция 6. Статические задачи нелинейной теории упругости.

6.1.Неупругие и нелинейно упругие системы. Упругие тела и системы делятся на два класса: линейно деформируемые и нелинейно деформируемые. У линейно деформируемых систем зависимость между внешними нагрузками (или вообще воздействиями) и перемещениями (или другими внутренними силовыми факторами) линейна, и все основные уравнения: равновесия, совместности деформаций и физические соотношения, - линейные. Для них справедлив принцип независимости действия сил (принцип наложения или суперпозиции): суммарный эффект от нескольких воздействий равен сумме эффектов от отдельных воздействий. Это относится к усилиям, деформациям, перемещениям и любым другим силовым характеристикам – конструкцию можно рассчитывать на отдельные единичные усилия, а затем результаты умножить на значения этих усилий и сложить друг с другом.

Например, перемещение какой-либо i- ой точки (или сечения) связано с действующими нагрузками зависимостью

w_i= , (6.1)

где – параметры, характеризующие внешние нагрузки; – коэффициенты влияния нагрузок на перемещения w_i, численно равные значению этого перемещения, вызванному действием соответствующей нагрузки при единичном значении характеризующего ее параметра =1. В случае нелинейно деформируемой системы значения коэффициентов влияния изменяются по мере изменения внешних нагрузок.

Нелинейная зависимость будет иметь место между прогибом консольной балки и приложенной на ее конце силой Р при больших прогибах. С ростом величины силы балка изгибается все больше и больше, что приводит к уменьшению плеча силы. В результате изгибающие моменты, а, значит, напряжения, деформации и перемещения будут возрастать медленнее, чем сила Р, т.е. зависимость между силой Р и перемещением конца балки будет нелинейной.

Большинство строительных материалов или совсем не подчиняется закону Гука, или подчиняется ему при напряжениях, не превосходящих предела упругости материала, в то время как в работе инженерных сооружений часто напряжения в отдельных точках или даже в целой области превосходят предел упругости и приближаются к пределу прочности материала.

Расчет конструкций за пределом упругости является значительно более сложным, чем в линейной постановке, поэтому в практике проектирования пока еще используют простые и хорошо разработанные методы линейной и теории упругости. Другая причина широкого применения расчета по упругой стадии – такой расчет полностью гарантирует безопасность конструкций как при однократных, так и при многократных и переменных воздействиях, что приводит к излишним запасам прочности и заведомому перерасходу материалов. Цель расчетов за пределом упругой работы конструкций – гарантировано, насколько это возможно, уменьшить этот перерасход, получив существенную экономию.

Основное, что отличает неупругую работу материала от упругой, - это отсутствие потенциала внутренних сил, обусловленное частичным рассеиванием механической энергии, которая переходит в другие виды энергии, и полностью не возвращается при разгрузке конструкции. Это наглядно видно на обычной диаграмме работы образца при растяжении или сжатии, т.е. зависимость «деформация – напряжение», форма кривой которой отвечает определенному режиму нагружения; при иных скоростях нагружения, остановках на этапах и т.п. вид диаграммы несколько меняется. При переходе же от нагружения к разгрузке и последующем нагружении диаграмма принимает совершенно другой вид. Следовательно, между напряжениями и деформациями за пределом упругости нет функциональной связи.

Очень важным в теории упругости, как линейной, так и нелинейной, является предположение о том, что внутренние упругие силы имеют потенциал, т.е. что работа упругих сил полностью затрачивается на формирование потенциальной энергии, накапливаемой телом при получении им упругих деформаций и возвращаемую ему в виде работы сил при исчезновении деформации. Это допущение – прямое следствие всеобщего закона сохранения материи (энергии), - позволяе т получать напряжения как частные производные от потенциальной энергии по соответствующим деформациям.

Гипотетически можно представить себе материал с нелинейной зависимостью напряжений от деформаций, который полностью при разгрузке возвращает накопленную механическую энергию. Диаграмма разгрузки для такого материала совпадает с диаграммой нагружения, и поглощения механической энергии не происходит. Если известно, что напряжения в конструкции в процессе ее нагружения нигде не будут уменьшаться, то можно условно считать, что конструкция выполнена из нелинейно упругого материала с криволинейной функциональной зависимостью ϭ=f(ε), совпадающей с диаграммой работы материала при нагружении. При этом становится возможным использование понятия потенциальной энергии системы.

Понятия нелинейно упругого материала и нелинейно упругой системы очень удобны для расчета неупругих систем при первичном их нагружении. Необходимо только следить, чтобы нигде не возникало уменьшения напряжений (об этом можно судить на основании расчета). При появлении уменьшения напряжений схема нелинейно упругой системы будет уже неприменима.

Нелинейности в поведении конструкций обусловлены главным образом одной из двух причин. Наиболее очевидной причиной является нелинейная зависимость напряжения от деформации для материала конструкции; в этом случае конструкция будет характеризоваться как физически нелинейная. Другой случай относится к такой нелинейности, которая обусловлена геометрией деформированной конструкции. Подобная ситуация возникает независимо от того, чем вызваны прогибы; примером является консольная балка, рассмотренная выше. Хотя материал балки подчиняется закону Гука, но из-за геометрии деформированной конструкции оказывается, что прогибы и напряжения связаны нелинейными соотношениями с приложенными нагрузками. Это пример так называемой геометрическоц нелинейности.

Независимо от того, какая – физическая или геометрическая – нелинейность имеет место, предполагаем, что материал конструкции остается упругим. Если это так, то дальнейшие выводы будут верны для любого числа нагружений конструкции. С другой стороны, для неупругого материала полученные результаты будут справедливы только на начальном этапе нагружения.

В частном случае, когда материал следует закону Гука и отсутствует геометрическая нелинейность, конструкция ведет себя как линейная и можно применять способ наложения. Имея дело с нелинейной конструкцией, необходимо постоянно учитывать, что способ наложения в общем случае не применим.

6.2. Зависимости нелинейной теории упругости. Геометрически нелинейные задачи возникают при исследовании напряженно-деформированного состояния тел, которые не обладают свойством относительной жесткости. В этом случае при выводе зависимостей между деформациями и перемещениями нельзя пренебрегать углами поворота элементов при вычислении их длины и линейными деформациями в выражениях для углов поворота. При выводе других основных уравнений нелинейной теории упругости следует учитывать изменение положения площадок в точке тела в результате деформации.

Если положение точек тела до деформации определяется декартовыми координатами 𝑥, , а после деформации соответственно координатами ξ, 𝜂, 𝜁 в той же координатной системе, то можно записать

ξ = 𝑥+𝑢(𝑥, 𝑦, 𝑧); 𝜂 = 𝑦+𝑣(𝑥, 𝑦, 𝑧); 𝜁 = 𝑧+𝑤(𝑥,𝑦,𝑧), (1)

где 𝑢, 𝑣, 𝑤 ˗ проекции координат точек тела, имевших до деформации координаты 𝑥, 𝑦, 𝑧.

Зависимости между перемещениями и деформациями нелинейно упругого тела имеют вид:

= ˗ 1,

………………………………………..,

= arcsin (2)

…………………………………………

Формулы для других линейных (, ) и угловых (, ) деформаций легко выписать по аналогии с выражениями (2).

Деформации не могут быть произвольными; они связаны между собой шестью условиями совместности деформаций. Ввиду достаточной громоздкости, мы не проводим здесь этих условий.

При больших деформациях размеры тела, размеры и ориентация бесконечно малых площадок могут существенно изменяться, что должно учитываться также при составлении уравнений равновесия.

Уравнения равновесия могут быть составлены по-разному: либо для элементарных объемов, грани которых перпендикулярны координатным осям до деформации, либо для элементарных объемов, грани которых перпендикулярны координатным осям после деформирования тела. Воспользовавшись вторым подходом, получим:

˗ уравнения равновесия элементарного параллелепипеда:

; (3)

˗ уравнения равновесия элементарного тетраэдра:

 

, (4)

 

где , , …, ˗ напряжения, действующие на площадках, перпендикуляр-

ных координатным осям после деформации тела; (ξ, 𝜂, 𝜁), (ξ, 𝜂, 𝜁), (ξ, 𝜂, 𝜁) ˗ объемные силы; ˗ направляющие косинусы к деформирован-

ной поверхности тела; ˗ составляющие интенсивности поверхностных сил. Все величины, входящие в уравнения равновесия, являются функциями координат точек тела после деформации ξ, 𝜂, 𝜁.

При решении задач теории упругости уравнения (3) и (4) должны быть преобразованы к переменным 𝑥, 𝑦, 𝑧 на основании зависимостей (1). Кроме того, от напряжений , , …, необходимо перейти к напряжениям , , …, , действующим по площадкам, перпендикулярным осям до деформации.

Если преобразованные указанным выше способом уравнения равновесия дополнить геометрическими уравнениями типа (2) и физическими уравнениями, связывающими напряжения и деформации (линейными или нелинейными), то полученная система уравнений будет достаточной для определения напряженно-деформированного состояния геометрически нелинейного тела. Однако практическое решение нелинейной задачи в общем случае значительно сложнее решения аналогичной линейной задачи.

Особенности отдельных задач позволяют упростить некоторые из основных уравнений нелинейной теории упругости. Так, если ограничиться рассмотрением деформаций, пренебрежимо малых, по сравнению с единицей, то формулы (2) можно упростить и привести к такому виду:

 

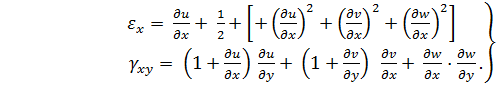(5)

 

Формулы для остальных четырех компонентов тензора деформаций могут быть выписаны по аналогии с выражениями (5).

Дальнейшие упрощения можно сделать в том случае, когда одно из перемещений и значения его производных на порядок превышают остальные. Такой случай имеет место при исследовании деформирования тонких пластин. Перемещения точек пластины в нормальном к ее плоскости направлении (𝑤) могут на порядок превышать перемещения в ее плоскости (𝑢, 𝑣). В результате выражения для компонентов деформаций (5) дополнительно упрощаются и принимают следующий вид:

 

(6)

 

Наконец, если все перемещения достаточно малы, то в формулах для деформаций можно было бы пренебречь квадратами и произведениями производных от перемещений по координатам по сравнению с их первыми степенями. При этом получим геометрические соотношения Коши линейной теории упругости.

Для МДТТ геометрически нелинейные зависимости представляют интерес в связи с задачами о напряженно- деформированных состояниях тонкостенных конструкций, об устойчивости таких состояний.

В заключение заметим, что принцип независимости действия сил (принцип наложения) в нелинейных задачах теряет силу. Поэтому расчет должен вестись при одновременном учете всех действующих на тело в рассматриваемый момент нагрузок.

6.3. Методы решения нелинейных задач. В нелинейно упругих системах внутренние силы (𝑗 = 1, 2 …, 𝑚), где 𝑚 ‒ число элементов системы, выражаются через деформации в общем случае системой нелинейных уравнений:

(6.3.1)

Уже составление этой системы уравнений, а тем более решение ее совместно с условиями равновесия и условиями неразрывности деформаций является делом довольно сложным, однако при наличии современной компьютерной техники вполне разрешимым. Во многих случаях, например при расчете стержневых систем, система уравнений (6.3.1) распадается на отдельные уравнения. Это бывает тогда, когда усилие в одном элементе зависит от деформации только этого элемента и не зависит от деформаций других элементов. Так, для ферм мы получаем

(6.3.2)

где и ‒ площади и длины стержней фермы; 𝑓 ‒ функция, выражающая зависимость напряжений 𝜎 от деформаций 𝜀 материала фермы;

𝜎 = 𝑓(𝜀), (𝜀 = 𝜆/𝑙).

Зависимости (6.3.2) легко обращаются при помощи обратной функции g, выражающей деформации через напряжения

𝜀 = g (𝜎),

и имеют вид

= g () = g ().

При помощи этих зависимостей легко решается задача расчета статически определимых ферм из нелинейно упругого материала, но при расчете статически неопределимых ферм здесь остаются еще значительные трудности.

 

Шаговый метод. Одним из эффективных методов расчета нелинейно упругих систем является шаговый метод, который заключается в следующем.

Будем нагружать нелинейно упругую систему постепенно, малыми порциями нагрузок 𝑃. При этом каждый раз будут получаться малые приращения деформаций, внутренних сил и перемещений. На этих малых перемещениях с достаточной точностью можно считать, что система ведет себя, как линейно упругая с коэффициентами упругости, зависящими от достигнутого уровня напряжений в элементах системы.

На первом этапе нагружения расчет на нагрузку 𝑃⁽¹⁾ ведется, как для обычной линейно упругой системы. Затем по усилиям в элементах, достигнутым в конце первого этапа, определяются зависимости между дальнейшими приращениями деформаций и усилий. Эти зависимости находятся путем дифференцирования соотношений (6.3.1):

……………………………………………..

Поскольку функции заданы, то производные также можно считать известными. Подставляя в эти производные значения деформаций в конце первого этапа нагружения, получаем коэффициенты линейных зависимостей усилий от деформаций на втором этапе нагружения:

, (𝑖, 𝑗 = 1, 2, …, 𝑚) (6.3.3)

Верхний индекс в скобках указывает на то, что данная величина относится к концу первого этапа нагружения.

Расчет на второй этап нагружения силами 𝑃⁽²⁾ теперь может производиться как для линейно упругой системы с зависимостями усилий от деформаций:

 

∆ = ∆ + ∆ + … + ∆ ;

∆ = ∆ + ∆ + … + ∆ ;

……………………………………………

∆ = ∆ + ∆ + … + ∆ .

 

Дифференциалы здесь приближенно заменяются конечными разностями ∆ и ∆ .

Деформации, полученные от первого этапа нагружения, суммируются с деформациями, вызванными первым его этапом. Суммарные деформации в конце второго этапа нагружения обозначаем .

Коэффициенты упругости для третьего этапа нагружения определяем по формулам:

(𝑖, 𝑗 = 1, 2, …, 𝑚)

и расчетом как линейно упругой системы с этими коэффициентами упругости получаем добавку к деформациям за счет третьего этапа нагружения.

Таким же способом поступаем и дальше, определяя каждый раз новые коэффициенты упругости , где 𝓀 ‒ число предшествующих этапов нагружения.

Приходится следить, чтобы все деформации и усилия с каждым этапом получали положительные приращения (или оставались без изменения), т. е. чтобы в системе нигде не возникала разгрузка. В противном случае схема нелинейно упругой системы будет неприменима. Впрочем, шаговый метод может быть применен и в этом случае, только в разгружаемых элементах коэффициенты упругости следует брать не по формулам (6.3.3), а как для линейно упругого материала.

После ряда нагружений может оказаться, что определить матрицы коэффициентов окажется равным нулю или, перейдя через нуль, станет отрицательным. Это будет означать, что несущая способность системы превышена. Таким образом, критерием разрушения системы будет служить равенство нулю этого определителя.

Точность расчета шаговым методом зависит от размеров шагов нагружения. При очень малых шагах увеличивается количество этапов, что ведет к уменьшению точности вычислений, точно так же, как и при чрезмерном уменьшении числа этапов, когда замена бесконечно малых приращений конечными может оказаться слишком грубой. Поэтому существует некоторый оптимум числа и размеров шагов нагружений, определяемый при составлении компьютерных программ более тонкими методами.

Метод упругих решений. Этот метод дает хорошие результаты при не слишком больших отклонениях работы материала от закона Гука. Система первоначально рассчитывается на заданную нагрузку как упругая с начальным модулем упругости. Получим значения усилий и деформаций . Затем по деформациям находим, пользуясь физической зависимостью между деформациями и усилиями, усилия . Последние, как правило, меньше усилий и не могут удержать заданную внешнюю нагрузку. Нетрудно с помощью уравнений равновесия найти нагрузку, уравновешивающую усилия . Вектор этой нагрузки обозначим ₁ , а вектор первоначально заданной нагрузки ₀ .

Рассчитаем теперь нашу систему на нагрузку, вектор которой представляет собой разность векторов ₀ ‒ ₁, по-прежнему считая систему упругой. Получим деформации ∆ и внутренние силы ∆ . Суммируя их с ранее найденными деформациями и усилиями , получим второе приближение для деформаций и усилий .

Далее поступаем так же, как после первого приближения: по деформациям и физическим зависимостям определяем усилия 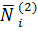и вектор нагрузки, уравновешивающий эти усилия ₂, вновь рассчитываем систему на нагрузку ₂ ‒ ₁ и добавляем полученные значения усилий и деформаций к ранее найденным значениям 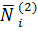и , получив таким образом третье приближение. Продолжив этот процесс, придем в случае его сходимости к истинным значениям усилий и деформаций. Условия сходимости данного процесса не вполне выявлены, и мы рассматривать их не будем.

Сходимость метода можно улучшить, если на каждом этапе рассчитывать систему на дополнительную нагрузку как упругую, но не с начальными модулями упругости, а с касательными, соответствующими достигнутым деформациям . В общем случае действительные нелинейные зависимости (6.3.1) здесь заменяются линейными, полученными разложением уравнений (6.3.1) в степенные ряды не в окрестностях нулевых деформаций 0, а в окрестностях деформаций ; Необходимость формирования каждый раз новой матрицы коэффициентов упругости затрудняет процесс вычислений, поэтому первый вариант метода упругих решений, несмотря на худшую сходимость, часто оказывается более предпочтительным.

 

Поделиться:

Воспользуйтесь поиском по сайту: