 |
Провести выбор и оценку поставщика с помощью экспертных методов для конкретного предприятия (рынка)
|
|
|
|
С помощью экспертных методов проведем выбор и оценку поставщика молочных продуктов для ООО "Сармас" (магазин "Валерия").
1. Оценка компетентности экспертов.
Постановка проблемы: Какому из ниже перечисленных поставщиков молочных продуктов магазин "Валерия" отдаст наибольшее предпочтение?
ГМЗ № 1;
ГМЗ № 2;
ГМЗ № 3;
Савушкин продукт;
Паркам-М;
Клецк МДК.
Была проведена взаимная групповая оценка компетентности экспертов, когда три эксперта оценивают каждого четвертого эксперта. Результаты оценки сведены в таблицу 1.
Таблица 1. Взаимные оценки экспертов
| № эксперта | Фамилия эксперта | № оцениваемого эксперта | |||
| 1 | 2 | 3 | 4 | ||
| 1 | Курдяев А.В. | - | 3 | 2 | 1 |
| 2 | Быков М.П. | 3 | - | 1 | 2 |
| 3 | Ахунов Р.А. | 3 | 2 | - | 1 |
| 4 | Шамрик Р.А. | 3 | 1 | 2 | - |
| Коллективное мнение группы, Кэi | 3 | 2 | 1,666 | 1,333 | |
| Место эксперта в ранжированном ряду | 1 | 2 | 3 | 4 | |
2. Определение коллективного мнения группы экспертов.
Таблица 2. Оценки экспертов в ранге
| Фамилия эксперта | Элементы (факторы) | Сумма рангов | |||||
| ГМЗ № 1 | ГМЗ № 2 | ГМЗ № 3 | Савушкин продукт | Паркам- М | Клецк МДК | ||
| Курдяев А.В. | 6 | 3 | 2 | 1 | 4 | 5 | 21 |
| Быков М.П. | 6 | 4 | 1 | 2 | 4 | 3 | 20 |
| Ахунов Р.А. | 5 | 3 | 2 | 1 | 6 | 4 | 21 |
| Шамрик Р.А. | 6 | 6 | 2 | 1 | 5 | 4 | 24 |
Оценки четырех экспертов в рангах по каждому элементу сведены в таблицу 2. При этом искусственно вводится условие, что, по крайней мере, в двух строчках должны быть одинаковые оценки двух или нескольких элементов (но не всех).
3. Нормировка рангов
Искусственно введенное условие привело к повторению рангов у двух экспертов. Это значит, что в оценках этих экспертов нарушено условие нормировки, когда сумма рангов по отдельным экспертам должна быть одинаковой и равной сумме членов натурального ряда, т.е.:
|
|
|
;
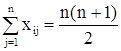где n - число элементов, подлежащих оценке.
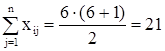
Для исправления этого положения произведем нормировку рангов. для этого: складывают места, которые занимают эксперты, имеющие одинаковые ранги, и полученную сумму делят на количество этих рангов. Полученные результаты сведены в таблицу 3.
Таблица 3. Оценки экспертов в ранге
| Фамилия эксперта | Элементы (факторы) | Сумма рангов | |||||
| ГМЗ № 1 | ГМЗ № 2 | ГМЗ № 3 | Савушкин продукт | Паркам-М | Клецк МДК | ||
| Курдяев А.В. | 6 | 3 | 2 | 1 | 4 | 5 | 21 |
| Быков М.П. | 6 | 4,5 | 1 | 2 | 4,5 | 3 | 21 |
| Ахунов Р.А. | 5 | 3 | 2 | 1 | 6 | 4 | 21 |
| Шамрик Р.А. | 4,5 | 4,5 | 2 | 1 | 5 | 4 | 21 |
| Среднее арифметическое мнение группы экспертов (хjср), ранги | 5,375 | 3,75 | 1,75 | 1,25 | 4,875 | 4 | 21 |
| Место элемента в ранжирован-ном ряду | 6 | 3 | 2 | 1 | 5 | 4 | |
4. Проверка согласованности показаний экспертов.
Групповая экспертная оценка может считаться надежной лишь при условии достаточной согласованности экспертов.
4.1 Проверка согласованности показаний экспертов с помощью коэффициентов ранговой корреляции Спирмена.
Порядок проверки:
4.1.1 Вычисляют отклонения между показаниями двух экспертов по каждому из сравниваемых элементов
4.1.2 Определяют квадрат указанных отклонений и их сумму
, 
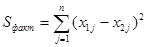
4.1.3 Вычисляют опытный коэффициент ранговой корреляции по формуле:
Проверка согласованности производится по следующему соотношению:
Если 
, то гипотеза о согласованности показаний экспертов не отвергается;
если 
то гипотеза о согласованности показаний экспертов отвергается.
При этом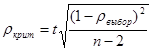 
,
где t = 2,78.
Полученные результаты сведены в таблицы.
Таблица 4. Попарная согласованность экспертов №1 и №2
| Фамилия эксперта | Элементы (факторы) | Сумма
| |||||
| ГМЗ № 1 | ГМЗ № 2 | ГМЗ № 3 | Савушкин продукт | Паркам-М | Клецк МДК | ||
| Курдяев А.В. | 6 | 3 | 2 | 1 | 4 | 5 | 8,5 |
| Быков М.П. | 6 | 4,5 | 1 | 2 | 4,5 | 3 | |
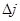
| 0 | -1,5 | 1 | -1 | -0,5 | 2 | |
| 0 | 2,25 | 1 | 1 | 0,25 | 4 | |
|
|
|
;
.
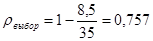Т.к.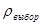 
> 
, то гипотеза о согласованности показаний экспертов №1 и №2 не отвергается.
Таблица 5. Попарная согласованность экспертов №1 и №3
| Фамилия эксперта | Элементы (факторы) | Сумма
| |||||
| ГМЗ № 1 | ГМЗ № 2 | ГМЗ № 3 | Савушкин продукт | Паркам-М | Клецк МДК | ||
| Курдяев А.В. | 6 | 3 | 2 | 1 | 4 | 5 | 6 |
| Ахунов Р.А. | 5 | 3 | 2 | 1 | 6 | 4 | |
| 1 | 0 | 0 | 0 | -2 | 1 | |
|
| 1 | 0 | 0 | 0 | 4 | 1 | |
;
.
Т.к. 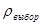> , то гипотеза о согласованности показаний экспертов №1 и №3 не отвергается.
Таблица 6. Попарная согласованность экспертов №1 и №4
| Фамилия эксперта | Элементы (факторы) | Сумма
| |||||
| ГМЗ № 1 | ГМЗ № 2 | ГМЗ № 3 | Савушкин продукт | Паркам-М | Клецк МДК | ||
| Курдяев А.В. | 6 | 3 | 2 | 1 | 4 | 5 | 6,5 |
| Шамрик Р.А. | 4,5 | 4,5 | 2 | 1 | 5 | 4 | |
|
| 1,5 | -1,5 | 0 | 0 | -1 | 1 | |
|
| 2,25 | 2,25 | 0 | 0 | 1 | 1 | |
;
.
Т.к. 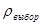> , то гипотеза о согласованности показаний экспертов №1 и №4 не отвергается.
Для данных табл.7:
;
.
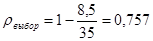Таблица 7. Попарная согласованность экспертов №2 и №3
| Фамилия эксперта | Элементы (факторы) | Сумма
| |||||
| ГМЗ № 1 | ГМЗ № 2 | ГМЗ № 3 | Савушкин продукт | Паркам-М | Клецк МДК | ||
| Быков М.П. | 6 | 4,5 | 1 | 2 | 4,5 | 3 | 8,5 |
| Ахунов Р.А. | 5 | 3 | 2 | 1 | 6 | 4 | |
|
| 1 | 1,5 | -1 | 1 | -1,5 | -1 | |
|
| 1 | 2,25 | 1 | 1 | 2,25 | 1 | |
Т.к. 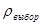> , то гипотеза о согласованности показаний экспертов №2 и №3 не отвергается.
Таблица 8. Попарная согласованность экспертов №2 и №4
| Фамилия эксперта | Элементы (факторы) | Сумма
| |||||
| ГМЗ № 1 | ГМЗ № 2 | ГМЗ № 3 | Савушкин продукт | Паркам-М | Клецк МДК | ||
| Быков М.П. | 6 | 4,5 | 1 | 2 | 4,5 | 3 | 5,5 |
| Шамрик Р.А. | 4,5 | 4,5 | 2 | 1 | 5 | 4 | |
|
| 1,5 | 0 | -1 | 1 | -0,5 | -1 | |
|
| 2,25 | 0 | 1 | 1 | 0,25 | 1 | |
;
.
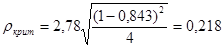Т.к. >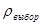 
, то гипотеза о согласованности показаний экспертов №2 и №4 не отвергается.
Таблица 9. Попарная согласованность экспертов №3 и №4
| Фамилия эксперта | Элементы (факторы) | Сумма
| |||||
| ГМЗ № 1 | ГМЗ № 2 | ГМЗ № 3 | Савушкин продукт | Паркам-М | Клецк МДК | ||
| Ахунов Р.А. | 5 | 3 | 2 | 1 | 6 | 4 | 3,5 |
| Шамрик Р.А. | 4,5 | 4,5 | 2 | 1 | 5 | 4 | |
|
| 0,5 | -1,5 | 0 | 0 | 1 | 0 | |
|
| 0,25 | 2,25 | 0 | 0 | 1 | 0 | |
;
.
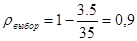Т.к. 
> , то гипотеза о согласованности показаний экспертов №3 и №4 не отвергается.
Полученные значения ранговой корреляции занесены в таблицу 10.
Таблица 10. Коэффициенты ранговой корреляции
| Фамилия эксперта | Эксперты | |||
| 1 | 2 | 3 | 4 | |
| Курдяев А.В. | 1 | 0,757 | 0,829 | 0,814 |
| Быков М.П. | 0,757 | 1 | 0,757 | 0,843 |
| Ахунов Р.А. | 0,829 | 0,757 | 1 | 0,9 |
| Шамрик Р.А. | 0,814 | 0,843 | 0,9 | 1 |
|
|
|
Вывод: Проверка согласованности экспертов методом определения ранговой корреляции показала высокую согласованность оценок экспертов, о чем свидетельствует коэффициенты ранговой корреляции, которые стремятся к 1.
4.2 Проверка согласованности показаний группы экспертов с помощью коэффициента конкордации Кендела.
4.2.1 Определяем сумму рангов по каждому из элементов
и общую сумму рангов по всем элементам
4.2.2 Вычисляем среднеарифметическое значение коллективного мнения группы.
4.2.3 Вычисляем среднее значение суммы рангов:
4.2.4 Вычисляем фактические отклонения поэлементных сумм рангов от среднего значения суммы рангов и их квадраты:
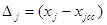
4.2.5 Определяем сумму квадратов отклонений
4.2.6 Вычисляем значение коэффициента конкордации Кендела
4.2.7 Вычисляем значение величины:
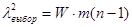
Если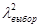 
> 
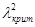, то гипотеза о согласованности показаний экспертов не отвергается;
если 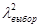< 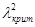то гипотеза о согласованности показаний экспертов отвергается.
Где 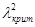-критическая точка распределения Пирсона;
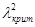=11,1
Результаты расчетов сводим в таблицу 11.
Таблица 11. Коэффициент конкордации Кендела
| Фамилия эксперта | Элементы (факторы) | Сумма рангов, Sфакт | |||||
| ГМЗ № 1 | ГМЗ № 2 | ГМЗ № 3 | Савушкин продукт | Паркам- М | Клецк МДК | ||
| Курдяев А.В. | 6 | 3 | 2 | 1 | 4 | 5 | 21 |
| Быков М.П. | 6 | 4,5 | 1 | 2 | 4,5 | 3 | 21 |
| Ахунов Р.А. | 5 | 3 | 2 | 1 | 6 | 4 | 21 |
| Шамрик Р.А. | 4,5 | 4,5 | 2 | 1 | 5 | 4 | 21 |
| xj | 21,5 | 15 | 7 | 5 | 19,5 | 16 | 84 |
| xjср | 5,375 | 3,75 | 1,75 | 1,25 | 4,875 | 4 | |
|
| 7,5 | 1 | -7 | -9 | 5,5 | 2 | |
|
| 56,25 | 1 | 49 | 81 | 30,25 | 4 | 221,5 |
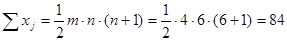
jср 
;
.
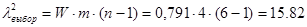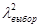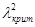> =11,1,
следовательно, гипотеза о согласованности показаний экспертов не отвергается.
Вывод: Проверка согласованности показаний группы экспертов с помощью коэффициента конкордации Кендела показала высокую оценку согласованности экспертов.
Полученный результат дает такое же значение, как и при использовании коэффициента ранговой корреляции, что говорит о взаимозаменяемости этих методов.
|
|
|
5. Определение коэффициентов относительной важности элементов
Предварительно переводим оценки, выраженные в рангах, в десятибалльную систему оценок.
Таблица 12. Перевод рангов в баллы
| Ранги | 1 | 2 | 3 | 4 | 4,5 | 5 | 5,5 | 6 |
| Баллы | 10 | 9 | 7 | 5 | 4 | 3 | 2 | 1 |
Таблица 13. Оценка экспертов в баллах
| Фамилия эксперта | Вес эксперта | Элементы | Сумма рангов, Sбал | |||||
| ГМЗ № 1 | ГМЗ № 2 | ГМЗ № 3 | Савушкин продукт | Паркам- М | Клецк МДК | |||
| Курдяев А.В. | 3 | 1 | 7 | 9 | 10 | 5 | 3 | 35 |
| Быков М.П. | 2 | 1 | 4 | 10 | 9 | 4 | 7 | 35 |
| Ахунов Р.А. | 1,666 | 3 | 7 | 9 | 10 | 1 | 5 | 35 |
| Шамрик Р.А. | 1,333 | 4 | 4 | 9 | 10 | 3 | 5 | 35 |
Определяем коэффициент относительной важности или значимость каждого элемента без учета компетентности экспертов по формуле:
;
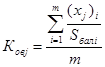
Определяем коэффициент относительной важности или значимость каждого элемента с учетом компетентности экспертов по формуле:
;
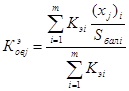Результаты расчетов сводим в таблицу 14.
Таблица 14. Относительная важность элементов
| Показатель | Элементы | |||||
| ГМЗ № 1 | ГМЗ № 2 | ГМЗ № 3 | Савушкин продукт | Паркам- М | Клецк МДК | |
| Место элемента в ряду | 6 | 3 | 2 | 1 | 5 | 4 |
| Ковj | 0,064 | 0,157 | 0,264 | 0,279 | 0,093 | 0,143 |
| Место элемента в ряду | 6 | 3 | 2 | 1 | 5 | 4 |
| Ковj | 0,055 | 0,164 | 0,264 | 0,279 | 0,102 | 0,136 |
| Место элемента в ряду | 6 | 3 | 2 | 1 | 5 | 4 |
Вывод: По результатам таблицы №14, оценки веса элементов и учета веса экспертов можно сделать вывод о том что, чем большее место в ряде занимает элемент, тем его оценка ниже. Учет веса экспертов позволяет уточнить и скорректировать оценки экспертов для получения наивысшей точности оценок. Использование коэффициента относительной важности эксперта позволяет уточнить значимость каждого элемента, и как следствие его место в ряду оценок.
|
|
|
12 |
