для студентов технических специальностей

 

 

САНКТ-ПЕТЕРБУРГ

УДК 530.10

 

 

Авторы:

Мустафаев А.С., Егоров С.В., Парфенова И.И., Пщелко Н.С., Смирнова Н.Н., Стоянова Т.В., Томаев В.В., Фицак В.В.

ЭЛЕКТРОДИНАМИКА. Сборник задачдля студентов технических специальностей. Санкт-Петербургский государственный горный институт (технический университет). С-Пб, 2010, C96.

Сборник задач охватывает основные разделы курса общая физика - II: Электрическое поле и его характеристики, теорема Остроградского – Гаусса для электрического поля в вакууме, проводники и диэлектрики в электрическом поле, энергия электрического поля, законы постоянного тока, электрический ток в газах и плазме, магнитное поле в вакууме, движущиеся заряды и проводники с токами в магнитном поле, магнитное поле в веществе, электромагнитная индукция. В каждом разделе сборника приведены основные понятия, законы и формулы, примеры решения задач, а также задания для самостоятельного решения.

Пособие отражает требования, предъявляемые к знаниям студентов технических специальностей вузов, и адресовано студентам всех специальностей СПГГИ (ТУ).

Авторы благодарны за помощь в создании оригинал макета сборника.

 

 

Табл. 19. Ил. 49.

 

Научный редактор доц. А.С. Мустафаев

 

© Санкт-Петербургский горный институт им. Г.В. Плеханова, 2010 г.

 

 

ОГЛАВЛЕНИЕ

 

Электростатика. 5

1. Взаимодействие заряженных тел. 5

основные формулы.. 5

примеры решения задач. 5

задачи для самостоятельного решения. 10

2. Напряжённость и потенциал электрического поля. Теорема Гаусса. 13

основные формулы.. 13

примеры решения задач. 16

задачи для самостоятельного решения. 23

3. Работа сил электрического поля. Энергия поля системы точечных зарядов. 28

основные формулы.. 28

примеры решения задач. 29

задачи для самостоятельного решения. 36

4. Электрическая ёмкость. Конденсаторы.. 39

основные формулы.. 39

примеры решения задач. 41

задачи для самостоятельного решения. 46

5. Постоянный электрический ток. 50

основные формулы.. 50

примеры решения задач. 52

задачи для самостоятельного решения. 56

Электромагнетизм.. 59

6. Магнитное поле постоянного тока. 59

основные формулы.. 59

примеры решения задач. 61

задачи для самостоятельного решения. 64

7. Сила, действующая на проводник с током в магнитном поле. 69

основные формулы.. 69

примеры решения задач. 69

задачи для самостоятельного решения. 72

8. Сила, действующая на заряд, движущийся в магнитном поле. 77

основные формулы.. 77

примеры решения задач. 77

задачи для самостоятельного решения. 80

9. Электромагнитная индукция. Индуктивность. 83

основные формулы.. 83

примеры решения задач. 85

задачи для самостоятельного решения. 87

 

ЭЛЕКТРОСТАТИКА

 

1. ВЗАИМОДЕЙСТВИЕ ЗАРЯЖЕННЫХ ТЕЛ

ОСНОВНЫЕ ФОРМУЛЫ

 

Закон Кулона:

где – сила взаимодействия точечных зарядов q ₁ и q ₂; r – расстояние между зарядами; – радиус-вектор, численно равный расстоянию между зарядами; e – диэлектрическая проницаемость среды; в которой находятся заряды, e ₀ – электрическая постоянная, e ₀ = 8,85×10^-12 Ф/м.

Закон сохранения заряда

где — алгебраическая сумма зарядов, входящих в изолированную систему; п – число зарядов.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

1. В центр квадрата, в каждой вершине которого находится заряд q= 2,33 нКл, помещен отрицательный заряд q₀. Найти этот заряд, если на каждый заряд q действует результирующая сила F = 0.

Решение:

Рассмотрим силы, действующие на любой из зарядов в вершинах, например, на заряд q₂ (см. рис.1). Coстороны зарядов q₁, q₃, q₄ на него действуют силы , и 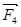соответственно, причем F₁=F₃= . Модуль силыдействующей на заряд q₂ со стороны заряда q₀, равен 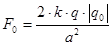. Условие равновесия заряда + + + 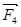=0 — (1). В проекции на ось х уравнение (1) имеет вид: , или .

Отсюда находим 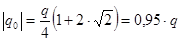; q₀ = –2,23 нКл.

Ответ: q₀ = –2,23 нКл.

 

2. В углах при основании равнобедренного треугольника с боковой стороной 8 см расположены заряды Q₁ и Q₂. Определить силу, действующую на заряд 1 нКл, помещенный в вершине треугольника. Угол при вершине 120°. Рассмотреть случаи:

a) Q₁ = Q₂ = 2 нКл

b) Q₁ =- Q₂ = 2 нКл

Дано: Кл; Кл; r = 0,08 м; a = 30°; e = 1, F₁ и F₂ -?.

Решение

В соответствии с принципом суперпозиции поле каждого из зарядов Q₁ и Q ₂ действует на заряд Q₃ независимо. Это значит, что на заряд Q₃ действуют силы, модули которых (рис.2)

, .

Так как , то . Векторная сумма является искомой величиной. Модуль силы определяется:

. В случае одноименных зарядов Q₁ и Q₂ из рис.2 видно, что угол b = 120°, поэтому :

;

Случай разноименных зарядов Q₁ и Q₂ представлен на рис. 3. Видно, что угол b равен 60° и, следовательно,

;

.

Ответ: .

 

3. Два маленьких одноименно заряженных шарика радиусом r = 1 см подвешены на двух нитях длиной l = 1 м. Заряды шариков q = 4×10^-6 Кл. Нити, на которых подвешены шарики, составляют угол a₁ = 90°.

1) Определить массу шариков.

2) Определить диэлектрическую проницаемость диэлектрика, если его плотность r = 8×10^-4 кг/м³ при условии, что при погружении шариков в жидкий однородный диэлектрик угол между нитями будет a₂ = 60°.

Дано: r = 1 см, q = 4×10^-6 Кл, a₁ = 90°, a₂ = 60°, r = 800кг/м³, l = 1 м; m -? e -?.

Решение

Очевидно, что условия равновесия для обоих шариков одинаковы, поэтому рассмотрим один из них. В воздухе на шарик действуют три силы (рис. 4): сила Кулона сила натяжения нити сила тяжести Условие равновесия шарика

,

или в проекциях на оси координат

на ось x: ,

на ось y:

.

Расстояние между шариками равно 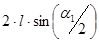. Модуль кулоновских сил определится формулой

.

Из написанной системы уравнений очевидно

,

и окончательно

,

,

.

 

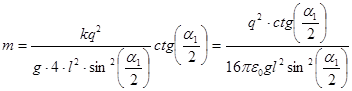В диэлектрике (рис. 5) на шарик действуют четыре силы: сила Кулона , сила натяжения нити , сила тяжести и выталкивающая сила, модуль которой F_выт=rVg, где V=(4/3)pr³ – объем шарика.

Условие равновесия для каждого шарика имеет вид

,

или в проекциях

на ось x: ,

на ось y: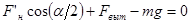

откуда

,

и, окончательно,

,

,

Ответ: e = 2.

4. В атоме водорода электрон движется по стационарной круговой орбите с угловой скоростью w = 10¹⁶ рад/с. Определить радиус орбиты.

Дано: w = 10¹⁶ рад/с, m_e = 9,1´10^-31 кг, q_e = -1,6´10^-19 Кл; r -?

Решение

Согласно модели Бора, в атоме существуют орбиты, двигаясь по которым электрон не излучает энергию. В задаче рассматривается такая орбита. На электрон действует кулоновская сила притяжения к протону . Силой тяжести электрона пренебрегаем, так как m_eg << F.

По второму закону Ньютона m_ea_n = F,

,

откуда

,

учитывая, что заряд протона по величине равен заряду электрона , получаем окончательно,

,

,

,

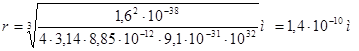Ответ:

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1.1. Два заряда находятся в керосине (e = 2) на расстоянии 1 см друг от друга и взаимодействуют с силой 2,7 Н. Величина одного заряда в 3 раза больше другого. Определить величину каждого заряда.

1.2. Два точечных заряда, находясь в воде (e₁ = 81) на расстоянии друг от друга, взаимодействуют с некоторой силой . Во сколько раз необходимо изменить расстояние между ними, чтобы они взаимодействовали с такой же силой в воздухе (e₂ = 1)?

1.3. Два шарика одинакового объема, обладающие массой 6·10^-4 г каждый, подвешены на шелковых нитях длиной 0,4 м так, что их поверхности соприкасаются. Угол, на который разошлись нити при сообщении шарикам одинаковых зарядов, равен 60°. Найти величину зарядов и силу электрического отталкивания.

1.4. В элементарной теории атома водорода принимают, что электрон вращается вокруг протона по окружности. Какова скорость вращения электрона, если радиус орбиты 5,3·10^-11 м?

1.5. Вычислить ускорение, сообщаемое одним электроном другому, находящемуся от первого в вакууме на расстоянии 1 мм.

1.6. Два равных по величине заряда 3×10^-9 Кл расположены в вершинах при острых углах равнобедренного прямоугольного треугольника на расстоянии см. Определить, с какой силой эти два заряда действуют на третий заряд 10^-9 Кл, расположенный в вершине при прямом угле треугольника. Рассмотреть случаи, когда первые два заряда одно- и разноименные.

1.7. Точечные заряды Q₁ =20 мкКл, Q₂ = -10 мкКл находятся на расстоянии d = 5 см друг от друга. Определить напряженность поля в точке, удаленной на r₁ = 3 см от первого и на r₂ = 4 см от второго заряда. Определить также силу , действующую в этой точке на точечный заряд Q = 1 мкКл.

1.8. Три одинаковых точечных заряда Q₁ = Q₂ = Q₃ = 2 нКл находятся в вершинах равностороннего треугольника со сторонами а = 10 см. Определить модуль и направление силы , действующей на один из зарядов со стороны двух других.

1.9. Два положительных точечных заряда Q и 9Q закреплены на расстоянии d = 100 см друг от друга.Определить в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.

1.10. Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол a. Шарики погружают в масло. Какова плотность r масла, если угол расхождения нитей при погружении в масло остается неизменным? Плотность материала шариков r_о = 1,5×10³ кг/м³, диэлектрическая проницаемость масла e = 2,2.

1.11. Четыре одинаковых заряда Q₁ = Q₂ = Q₃ = Q₄ = 40 нКл закреплены в вершинах квадрата со стороной а =10 см. Найти силу , действующую на один из этих зарядов со стороны трех остальных.

1.12. Точечные заряды Q₁ =30 мкКл и Q₂ = -20 мкКл находятся на расстоянии d = 20 см друг от друга. Определить напряженность электрического поля в точке, удаленной от первого заряда на расстояние r₁ = 30 см, а от второго - на r₂ = 15 см.

1.13. В вершинах правильного треугольника со стороной а = 10 см находятся заряды Q₁ = 10 мкКл, Q₂ = 20 мкКл и Qз= 30 мкКл. Определить силу , действующую на заряд Q₁ со стороны двух других зарядов.

1.14. В вершинах квадрата находятся одинаковые заряды Q₁ = Q₂ = Q₃ =Q₄ = 8×10^-10 Кл. Какой отрицательный заряд Q нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?

1.15. На расстоянии d = 20 см находятся два точечных заряда: Q₁ = -50 нКл и Q₂ = 100 нКл. Определить силу , действующую на заряд Qз = -10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.

1.16. Расстояние d между двумя точечными зарядами Q₁ = 2 нКл и Q₂ = 4 нКл равно 60 см. Определить точку, в которую нужно поместить третий заряд Q₃ так, чтобы система зарядов находилась в равновесии. Определить заряд Q₃ и его знак. Устойчивое или неустойчивое будет равновесие?

1.17. Два отрицательных точечных заряда Q₁ = -Q и Q₂ = -9Q закреплены на расстоянии d = 10 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд Q₃ так, чтобы система зарядов находилась в равновесии. Указать какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закреплённые заряды

1.18. На расстоянии d = 10 см находятся два точечных заряда: Q₁ = -50 нКл и Q₂ = 100 нКл. Определить силу , действующую на заряд Q₃ = -10 Кл, удалённый от первого заряда на расстоянии d и от второго заряда на расстояние 2d.

1.19. Три одинаковых отрицательных точечных заряда Q₁ = Q₂ = Q₃ = -2 нКл находятся в вершинах равностороннего треугольника со сторонами а = 20 см. Определить модуль, направление силы F, действующей на один из зарядов со стороны двух других.

1.20. В трёх вершинах квадрата со стороной 0,4 м находятся одинаковые отрицательные заряды по 5×10^-9 Кл каждый. Найти напряжённость и потенциал поля в четвёртой вершине квадрата.

1.21. Во сколько раз сила гравитационного притяжения между двумя протонами меньше силы их электростатического отталкивания? Заряд протона равен по модулю и противоположен по знаку заряду электрона.

1.22. Два шарика одинаковых радиуса и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. После сообщения шарикам заряда q₀ = 0,4 мкКл они оттолкнулись друг от друга и разошлись на угол 2α = 60°. Найти массу m каждого шарика, если расстояние от центра шарика до точки подвес l = 20 см.

1.23. Два шарика одинаковых радиуса и массы подвешены на нитях одинаковой длины так, что их поверхности соприкасаются. Какой заряд q нужно сообщить шарикам, чтобы сила натяжения нитей стала равной T = 98 мН? Расстояние от центра шарика до точки подвеса l = 10 см; масса каждого шарика m = 5 г.

1.24. Маленький шарик массой 2·10^-3 кг, подвешенный на тонкой шелковой нити, несет на себе заряд 3·10^-7 Кл. На какое расстояние снизу к нему следует поднести другой маленький шарик с зарядом 5·10^-5 Кл, чтобы натяжение нити уменьшилось в 2 раза?

1.25. В простейшей модели атома водорода предполагается, что электрон движется вокруг ядра по круговой орбите со скоростью 1.1´10⁶ м/c. Чему равен радиус орбиты?

2. НАПРЯЖЁННОСТЬ И ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ТЕОРЕМА ГАУССА.

ОСНОВНЫЕ ФОРМУЛЫ

Напряжённость электрического поля и потенциал:

,

где - сила, действующая со стороны электрического поля на заряд q, находящийся в данной точке поля.

Напряженность поля точечного заряда .

Принцип суперпозиции электростатических полей: напряженность поля создаваемого несколькими точечными зарядами находится как векторная сумма полей создаваемых каждым зарядом в отдельности.

Поток вектора напряженности однородного электрического поля через произвольную малую площадку DS равен , где a - угол между вектором E и нормалью к поверхности (см. рис 6).

По теореме Гаусса поток напряженности сквозь любую замкнутую поверхность

,

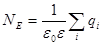где 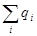- алгебраическая сумма свободных зарядов, находящихся внутри этой поверхности.

Поток электрического смещения сквозь любую замкнутую поверхность

.

При помощи теоремы Гаусса можно найти напряженность электрического поля, образованного различными заряженными телами.

Модуль напряженности поля, образованного заряженной бесконечно длинной нитью,

,

где t - линейная плотность заряда на нити, r – расстояние от нити.

Модуль напряженности поля, образованного заряженной бесконечно протяженной плоскостью,

 

 

,

где s - поверхностная плотность заряда на плоскости.

Модуль напряженности поля, образованного разноименно заряженными параллельными бесконечными плоскостями (поля плоского конденсатора),

.

Модуль напряженности поля, образованного заряженным шаром,

,

где q – заряд шара радиусом R и r – расстояние от центра шара, причем r > R..

Разность потенциалов между двумя точками электрического поля определяется работой, которую надо совершить, чтобы единицу положительного заряда принести из одной точки в другую:

.

Потенциал поля точечного заряда

,

где r – расстояние от заряда.

Напряженность электрического поля и потенциал связаны соотношением

.

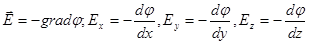ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

1. Определите зависимость напряженности электрического поля диполя от расстояния до него 1) на оси симметрии диполя, 2) на оси самого диполя.

Решение

Диполь представляет собой два точечных разноименных заряда +q и –q, равных по величине, расстояние между которыми мало и равно l.

Выберем оси x и y, как показано на рис. 7. Определим напряженность электрического поля диполя, используя принцип суперпозиции полей.

Найдем зависимость напряженности на оси симметрии, т.е. при x = 0.

Напряженность поля , создаваемого зарядом +q, равна , где ; напряженность поля , создаваемого зарядом – q, равна по величине . Тогда 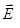= + . На рис.7 видно, что вектор 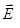параллелен оси x. Величи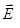на равна

,

где . Отсюда

.

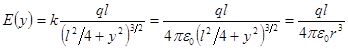Заметим, что напряженность поля диполя убывает быстрее, чем напряженность поля точечного заряда.

Определим зависимость напряженности от x при y = 0. Напряженность поля, созданного зарядом +q, равна

,

зарядом –q

.

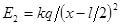Суммарная напряженность в проекции на ось x имеет вид 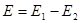. Подставляя выражения для E₁ и E₂, имеем

.

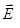Такие значения напряженности справедливы при . При напряженность равна , , . Окончательно,

.

 

2. Положительный заряд Q равномерно распределен по тонкому проволочному кольцу радиуса R. Определить напряженность поля и потенциал в точке C, лежащей на оси кольца на расстоянии z от его центра.

Дано: Q, R, z, E(z) -?, j(z) -?

Решение

Поле создано зарядом, распределенным по тонкому кольцу заданного радиуса. Оно не обладает достаточной симметрией даже при равномерном распределении заряда (нельзя указать точную конфигурацию силовых линий), поэтому для расчета напряженности и потенциала поля можно использовать только принцип суперпозиции.

Разобьем кольцо на элементарные участки (рис.8) Каждый такой участок можно принять за точечный заряд dQ. Потенциал созданного им поля

, (1)

где r – расстояние от элемента dQ до точки С.

Потенциал результирующего поля получим интегрированием выражения (1):

. (2)

Если ввести оси координат, то проекции вектора напряженности на оси координат можно определить дифференцированием полученного выражения для потенциала по соответствующей координате.

При переходе от одного элемента кольца к другому не изменяется. Тогда выражение (2) можно преобразовать:

.

Очевидно, что 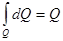независимо от характера распределения заряда. Следовательно, как и в случае равномерного распределения заряда по кольцу, так и в любом другом случае в точках, лежащих на оси кольца, потенциал

.

Проекция вектора напряженности на ось OZ.

.

При равномерном распределении заряда из симметрии следует, что вектор 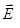, направлен вдоль оси OZ, т.е. E_x = E_y =0. При z > 0, если заряд положительный, E_z >0 и вектор 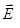направлен по оси OZ, т.е. вверх. В области z < 0, E_z < 0 и вектор 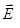направлен против оси OZ, т.е. вниз.

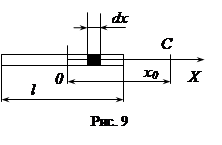3. Тонкий стержень длины l = 10 см равномерно заряжен зарядом Q = -3×10^-9 Кл (рис.9). Найти напряженность поля и потенциал в точке C, лежащей на оси стержня. Расстояние от середины стержня до этой точки x₀ = 20 см.

Дано: l = 10 см, Q = -3×10^-9 Кл, x₀ = 20 см, E(x₀) -?, j(x₀) -?

Решение

Электростатическое поле создано зарядом, распределенным по тонкому стержню. Конфигурация зарядов не позволяет установить точное расположение силовых линий в пространстве, поэтому для определения характеристик поля следует использовать принцип суперпозиции. Разобьем стержень на элементарные участки длины dl c зарядом dQ. Каждый такой участок можно принять за точечный заряд, создающий потенциал

,

где r – расстояние от элемента dl до точки C.

Потенциал результирующего поля

, (1)

где (Q) показывает, что интеграл берется по всему заряду Q, создающему поле. Поскольку требуется найти напряженность и потенциал поля в точках, лежащих на оси стержня, введем ось OX. Тогда длина элемента dl = dx, положение элемента определяется его координатой x, а расстояние от этого элемента до точки C

. (2)

Вследствие симметрии, очевидно, что в точках, лежащих на оси OX, вектор 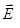направлен вдоль этой оси, поэтому

.

Равномерное распределение заряда по стержню позволяет утверждать, что , откуда .

Так как и при интегрировании по стержню переменная x изменяется в пределах от ‑l/2 до l/2, то согласно (1) и (2)

. (3)

Производя интегрирование получим:

. (4)

Для x₀ = 20 см j₀ = -138 В.

Расстояние х₀ в выбранной системе координат представляет собой абсциссу x точки C, и выражение (4) можно записать в виде

.

Тогда,

.

Поскольку заряд Q < 0, то E_x < 0 и E = - E _x,, если x > l/2 (справа от стержня), E_x > 0 и E = E _x, если x < l/2 (слева от стержня). Следует заметить, что формулы, выведенные для потенциала и напряженности, справедливы только для .

Подставляя x = x₀ = 20 см в (5), получаем E₀ = 720 В/м, причем вектор направлен против оси OX.

Ответ: j₀ = -138 В, E₀ = 720 В/м.

 

4. Пользуясь теоремой Гаусса, определить напряженность поля и потенциал заряженного по объему шара. Радиус шара R, объемная плотность заряда в шаре - r. Нарисовать графики E(r) и j(r).

Решение:

Пусть точка наблюдения находится внутри шара на расстоянии r < R от центра шара. Проведем мысленно сферу радиусом r вокруг центра шара O. Исходя из симметрии задачи. напряженность поля будет направлена вдоль радиуса шара и будет постоянной по величине на сфере радиуса r. При этом она все время будет перпендикулярна поверхности данной сферы (cм. рис. 10)

Чтобы сосчитать поток вектора напряженности через эту сферу, разобьем ее мысленно на участки DS, настолько малые, что их можно считать плоскими, а электрическое поле однородным (одинаковым по величине и направлению) в пределах каждого участка. Как мы указывали, напряженность поля направлена вдоль радиусов и, значит, перпендикулярно каждому из этих малых участков. Поток электрического поля через каждый участок DS оказывается равным . Полный поток вектора электрической напряженности через сферу 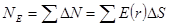. Здесь суммирование ведется по сфере и величина вектора электрической напряженности остается постоянной для всех слагаемых. Это дает возможность вынести E(r) из-под знака суммирования. , где S – площадь сферы радиуса r. И мы получаем . По теореме Гаусса поток вектора напряженности через замкнутую поверхность пропорционален электрическому заряду ограниченному данной поверхностью (см. ОСНОВНЫЕ ФОРМУЛЫ). Заряд, ограниченный сферой радиуса r 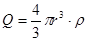, где r - объемная плотность. По теореме Гаусса , где e₀ - диэлектрическая проницаемость вакуума, e - диэлектрическая проницаемость среды содержащей заряды. Положим без потери общности рассмотрения e = 1. Подставляя сюда выражение для N_{E ,} получаем . Отсюда получаем .

Рассмотрим точку на расстоянии r > R от центра шара. Построим мысленно сферу радиуса r вокруг шара. Исходя из симметрии задачи, можно предположить, что напряженность поля направлена вдоль радиуса шара и остается постоянной во всех точках мысленно построенной сферы. Тогда аналогично вышеописанному случаю поток вектора электрической напряженности через эту сферу . Сфера окружает шар с зарядом , где R – радиус шара. Согласно теореме Гаусса 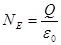. Подставляя выражения для потока и заряда, получаем . Отсюда получаем .

Для нахождения потенциала поля j(r) воспользуемся определением. Потенциал – это работа сил электрического поля по перенесению единичного положительного заряда из точки наблюдения на бесконечность. Это дает . Если r < R, то интеграл распадается на два . Подставляя сюда выражения для E(r), получаем . Вычисляя интегралы, получаем Если r > R, то , подставляя E(r) для случая r > R, получим . Вычисляя интеграл, получаем . Графики функций E(r) и j(r) приводятся на рисунке 11.

 

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

 

2.1. На расстоянии 8 см друг от друга в воздухе находятся два заряда по 1 нКл. Определить напряженность и потенциал поля в точке находящейся на расстоянии 5 см от зарядов.

2.2. Заряды по 1 нКл помещены в вершинах равностороннего треугольника со стороной 0,2 м. Равнодействующая сил, действующих на четвертый заряд, помещенный на середине одной из сторон треугольника, равна 0,6 мкН. Определить этот заряд, напряженность и потенциал поля в точке его расположения.

2.3. Два одинаковых заряда находятся в воздухе на расстоянии 0,1 м друг от друга. Напряженность поля в точке, удаленной на расстоянии 0,06 м от одного и 0,08 м от другого заряда, равна 10 кВ/м. Определить потенциал поля в этой точке и значение заряда.

2.4. Электрон движется по направлению силовых линий однородного поля напряженностью 2,4 В/м. Какое расстояние он пролетит в вакууме до полной остановки, если его начальная скорость 2×10⁶ м/с? Сколько времени будет длиться полет?

2.5. Две бесконечно длинные, равномерно заряженные нити с линейной плотностью зарядов 6×10^-5 Кл/м расположены на расстоянии 0,2 м друг от друга. Найти напряженность электрического поля, созданного в точке, удаленной на 0,2 м от каждой нити.

2.6. Тонкий стержень длиной l = 20 см несет равномерно распределенный заряд Q = 0,1 мкКл. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а = 20 см от его конца.

2.7. По тонкому полукольцу радиуса R = 10 см равномерно распределен заряд с линейной плотностью t = 1 мкКл/м. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.

2.8. Тонкое кольцо несёт распределенный заряд Q = 0,2 мкКл. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке А, равноудаленной от всех точек кольца на расстояние r = 20 см. Радиус кольца R=10 см.

2.9. Треть тонкого кольца радиуса R = 10 см несет распределенный заряд Q = 50 нКл. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.

2.10. Бесконечный тонкий стержень, ограниченный с одной стороны, несет равномерно распределенный заряд с линейной плотностью t = 0,5 мкКл/м. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке A, лежащей на оси стержня на расстоянии а = 20 см от его начала.

2.11. По тонкому кольцу радиусом R = 20 см равномерно распределен с линейной плотностью t = 0,2 мкКл/м заряд. Определить напряженность электрического поля, создаваемого распределенным зарядом в точке А, находящейся на оси кольца на расстоянии h = 2R от его центра.

2.12. По тонкому полукольцу равномерно распределен заряд Q = 20 мкКл с линейной плотностью t = 0,1 мкКл/м. Определить напряженность