 |
Величины степени и сравнения
|
|
|
|
Относительные величины степени и сравнения позволяют сопоставлять различные показатели в целях выявления, какая величина и на сколько больше другой, в какой мере одно явление отличается от другого или схоже с ним, что имеется общего и отличительного в наблюдаемых статистических процессах и т.д. Сравнительный анализ количественных показателей – один из важных приемов в юридической практике статистических обобщений. Он сопровождает все виды относительных и средних величин. В той или иной мере мы апеллировали к методам сравнения при рассмотрении аналитических возможностей относительных величин распределения, интенсивности, динамики.
1 Показатели распределения или структуры совокупности обычно измеряются в процентах удельных весов и открывают большие возможности для сопоставлений.
2 Показатели отношения части к целому, или отношения интенсивности, чаще всего измеряются в коэффициентах (в числе преступлений, осужденных, дел, исков и т.д.) на 100 тыс. населения. Этот относительный показатель был разработан не только для более объективной оценки массовых явлений, но и для сравнения несопоставимых абсолютных величин. Несопоставимые сведения о деятельности юридических учреждений, гражданском и уголовном судопроизводстве, судимости, преступности, правонарушаемости, зафиксированные в разных странах, регионах, районах и населенных пунктах, после пересчета на население становятся более или менее сопоставимыми и сравнимыми.
Средняя арифметическая величина
Средняя арифметическая является наиболее распространенным видом степенных средних, используется в случаях, когда объём усредняемого признака является аддитивной величиной, т.е. образуется как сумма его значений по всем единицам статистической совокупности. При этом если индивидуальные значения признака у статистических единиц заменить средней арифметической, то суммарный объем признака по совокупности в целом сохраняется неизменным. Это означает, что средняя арифметическая есть среднее слагаемое.
|
|
|
Средняя арифметическая простая используется при работе с несгруппированными данными и рассчитывается по формуле:

Если в исходных данных отдельные значения усредняемого признака повторятся, то расчет средней проводится по сгруппированным данным или вариационным рядам. В подобных случаях для расчета необходимо применять среднюю арифметическую взвешенную – среднюю сгруппированных величин.
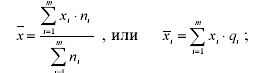
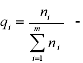
частость, т. е. удельный вес статистических единиц, обладающих определенным значением признака в общем объеме совокупности.
Средняя арифметическая обладает рядом полезных свойств, к важнейшим из которых относятся:
1. Средняя арифметическая постоянной величины равна этой величине:
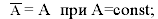
2. Алгебраическая сумма отклонений вариант от их средней арифметической равно нулю:
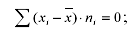
3. Если все варианты уменьшить (увеличить) на постоянное число А, то средняя арифметическая из них уменьшится (увеличится) на это же число:
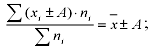
4. Если все варианты одинаково увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз:
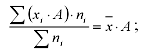
5. Если все веса средней одинаково увеличить (уменьшить) в несколько раз, то средняя арифметическая не изменится

Практическая часть
Задание 7




Задание 8
Сроки рассмотрения уголовных дел, рассматриваемых одним судом характеризуются следующим образом:
До 3 дней – 360 дел
От 3 до 5 дней – 90 дел
|
|
|
От 5 до 10 дней – 70 дел
От 10 до 20 дней – 170 дел
Сведем все вышеперечисленные показатели в таблицу:
| № группы | Сроки рассмотрения уголовных дел, дн. | Количество дел | Середина интервала | |
| x | f | x` | xf | |
| I | До 3 | 360 | 2 | 720 |
| II | 3—5 | 90 | 4 | 360 |
| Ш | 5—10 | 70 | 8 | 560 |
| IV | 10—20 | 170 | 15 | 2550 |
| Итого
| 690 | - | 4190 | |
В данном случае применим расчет средней арифметической взвешенной, которая определяется по формуле:
S хf
х = ¾¾¾¾,
Sf
Тогда, средний срок рассмотрения дела составляет:
4120
х = ¾¾¾¾ = 6 дней
690
Список литературы
1. Ефимова М.Р. и др. Общая теория статистики. Учебник. М.:, Финансы и статистика, 2002.
2. Теория статистики: Учебник / Под ред. Р.А. Шмойловой. М.:, Финансы и статистика, 2001.
3. Практикум по теории статистики. Учебное пособие / Под ред. Р.А. Шмойловой. М.:, Финансы и статистика, 2006.
4. Елисеева И.И., Юзбашев М.М. Общая теория статистики, М.: Финансы и статистика, 2002.
5. Статистика. Учебник для вузов / Под ред. И.И. Елисеевой. М.: Проспект. 2002
6. Курс социально-экономической статистики /Под ред. Назарова М.П. – М.: Финстатинформ, 2002.
7. Практикум по социальной статистике / Под ред. И.И. Елисеевой. М.: Финансы и статистика. 2006.
8. Ефимова М.Р., Бычкова А.Ю. Социальная статистика. Учебное пособие. М.: Финансы и статистика. 2002.
9. Харченко Л.П. Статистика: Учебное пособие для вузов. М.: Инфра – М. 2005.
10. Годин А.М. Учебник для вузов. М.: ИД Дашков и К,2002
11. Общая теория статистики /Под ред. Спирина А.А., Башиной О.Э., - М.: Финансы и статистика, 2007.
12. Методологические положения по статистике – М.: Госкомстат РФ, 1996
|
|
|


