 |
Примитивный элемент поля и циклическая группа
|
|
|
|
Предисловие
На сегодняшний день одна из самых крупных таблиц содержащих параметры двоичного циклического кода представлена в [1] и часть таблиц в приложении. Построение кода, при помощи данных указанных в таблице, не имея представлений о математическом описании циклических кодов проблематично. Данная работа будет полезна тем, кому необходимо использовать циклические коды в прикладных целях, а, следовательно, нет необходимости глубоко изучать их структуру. В рамках данной работы не рассматриваются алгоритмы кодирования и декодирования, а только алгоритм построения порождающего полинома циклического кода.
Краткие теоретические сведения
Полиномиальное представление двоичных чисел
Весьма удобным является представление двоичных чисел в виде полиномов степени n -1, где n – количество разрядов числа.
Идея представления числа в виде полинома состоит в следующем – основание системы счисления заменяется некоторой фиктивной переменной, например x. Степень этой переменной будет соответствовать номеру разряда числа, а коэффициент значению самого разряда. Рассмотрим пример: Запишем двоичное число и его разложение в виде степеней двойки (аналогично переводу в десятичную систему счисления): 
. Теперь, заменим двойку на фиктивную переменную x, при этом получим выражение: 
.
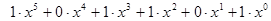Исключив элементы с нулевым коэффициентом, получим полиномиальное представление числа: 
.
Циклический код
Циклические коды относят к классу линейных кодов. Для обеспечения коррекции ошибок к блоку информационных разрядов добавляется блок контрольных разрядов. Значения контрольных разрядов формируются путем некоторых линейных операций над информационными разрядами, поэтому такие коды называются линейными. Линейный код называется циклическим, если слово 
принадлежит данному коду, и слово 
также принадлежит этому коду. Проще говоря, если циклически сдвинуть кодовую комбинацию, то в результате также получится кодовая комбинация, принадлежащая данному коду. Это самое важное свойство циклических кодов. Циклический код задается при помощи порождающего полинома g(x). На сегодняшний день существуют таблицы с параметрами кода - длина, мощность корректирующая способность и корни порождающего полинома. Порождающий полином, как правило, представлен в виде степеней его корней. Обозначим за n длину кода, если длину n можно представить в виде 
, где m – целое положительное число, то такой код называют кодом с тривиальной длиной.
|
|
|
Поле
Поле – это множество элементов замкнутое относительно двух бинарных операций – умножения и сложения. Под замкнутостью нужно понимать, что результат выполнения операций не выходит за пределы поля. Для поля выполняются следующие аксиомы:
1. Операция умножения обозначается как 
, сложение, как 
.
2. Результатом умножения и сложения элементов поля является элемент также из этого поля.
3. Для любого элемента поля не равного нулю, существует обратный элемент по сложению и умножению, так что 
и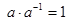 
4. Поле всегда содержит мультипликативную единицу 1, так что 
и аддитивную единицу 0, так что 
.
5. Для умножения и сложения выполняются правила ассоциативности, коммутативности и дистрибутивности.
Поля Галуа
Конечное поле или поле Галуа – это поле (далее конечное поле обозначено, как GF(p)), содержащее конечное число элементов. Нужно отметить, что аксиомы 1 – 5, справедливы, как для поля с конечным числом элементов, так и с бесконечным, но главное отличие конечных полей от бесконечных определяет аксиома 2. Из этого вытекает, что на понятие «умножение» и «сложение» накладывается ряд ограничений. Выполнение аксиомы 2 осуществляется выполнением по модулю некоторого числа p, называемым характеристикой поля.
|
|
|
Конечные поля существуют не при любом числе элементов, а только когда количество элементов поля – простое число p или его степень pm, где m – целое положительное число. В первом случае поле называется простым и обозначается, как GF(p), а во втором называется расширением простого поля и обозначается GF(pm).
Рассмотрим некоторое поле GF(p). Такое поле содержит p элементов, операции сложения и умножения над элементами этого поля производятся по модулю числа p. Рассмотрим расширение этого поля - GF(pm). Элементами 
расширения поля будут являться полиномы степени 
и меньше, с коэффициентами из поля GF(p). Приведем аналогию - простое поле содержит буквы алфавита, а расширение этого поля содержит слова определенной длины, составленные по некоторым правилам из букв, лежащих в основном поле.
Примитивный элемент поля и циклическая группа
Основное свойство конечных полей – это связь между собой ненулевых элементов поля 
и возможность их выражения через степень элемента 
, называемого примитивным, это означает, что любой элемент поля можно представить, как степень примитивного элемента, т.е.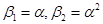 
и т.д. Множество 
элементов расширения поля образуют циклическую мультипликативную группу. Это означает, что все элементы расширения находятся в следующем отношении: 
. Таким образом, умножая элемент на себя можно получить любой элемент расширения поля (мультипликативность), но очевидно, что правило умножения должно быть специфическим, иначе, невозможно обеспечить нужную степень полинома и обеспечить цикличность, т.е. после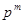 
умножений начнется повторение.
Правило умножения в расширении поля аналогично правилу умножения многочленов с последующим приведением по модулю некоторого специального полинома 
степени m. Приведение означает деление результата умножения на полином и использованию только остатка от деления, нужно отметить, что при делении сложение производится по правилам для основного поля, т.е. сложение проводится по модулю числа p.
Выше было сказано, что полином должен быть специальным, это означает, что любые операции, выполняемые по модулю должны оставаться обратимыми, иначе система не образует поле. Таким образом, полином 
должен быть неприводимым в поле GF(p), т.е. его нельзя разложить на множители, используя только многочлены с коэффициентами из поля GF(p). Аналогом неприводимого полинома является простое число. На сегодняшний день не существует систематического способа поиска неприводимых полиномов. Наиболее обширная таблица неприводимых полиномов представлена в книге [1].
|
|
|
Резюме: Расширение поля содержит полиномы степени m-1 и меньше, с коэффициентами из основного поля. Любой элемент расширения поля можно получить, как степень примитивного элемента 
. Умножение проводится по модулю неприводимого над полем GF(p) полиномом. Описанная выше теория может показаться запутанной, но ниже будет дан пример, который поможет понять изложенные теоретические сведения.
|
|
|
