монохроматических световых полей

Пространственная когерентность

Рис. 1. Схема опыта Ллойда.

Ухудшение видности интерференционной картины, связанное с конечными размерами источника, можно пояснить на примере опыта Ллойда (рис.1).

В опыте Ллойда когерентными являются источник S и его изображение S¢ в плоском зеркале М. Если точечный источник света излучает монохроматические волны длины l, то ширина интерференционной полосы (расстояние между точками экрана с максимальными I _max или минимальными I _min интенсивностями) определяется соотношением:

, (1)

где j - угол между волновыми векторами и , h - расстояние от источника до поверхности зеркала, L - расстояние от источника до экрана.

Видность интерференционной полосы в этом случае (считаем, что когерентные источники одинаковы) равна 1.

Интервал длин волн, испускаемых реальным источником, будем считать малым для того, чтобы степень временной когерентности была достаточной для получения четкой интерференционной картины.

Отдельные участки протяженного источника света (например, S₁ и S₂ на рис.2) излучают волны, фазы которых не связаны между собой. Наблюдаемая на экране интерференционная картина в схеме Ллойда с таким источником, является наложением картин, создаваемых каждым участком в отдельности. Их нулевые максимумы (точки экрана, для которых разность хода лучей равна нулю) совпадают (точка О на рис.2).

Рис.2. Размывание интерференционных полос при использовании протяженного источника.

Поскольку ширины интерференционных полос 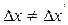(см. соотношение (1), в котором 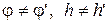), то видность V результирующей картины будет ухудшаться с возрастанием номера полосы.

Как видность V связана с размерами протяженного источника?

Рис.3. К определению разности хода лучей 1 и 2.

Пусть имеется равномерно светящаяся щель АВ ширины D (рис.3), расположенная перпендикулярно плоскости рисунка.

Направим ось X вдоль АВ и поместим начало отсчета в середине АВ. Один элементарный источник ширины dx создает на экране интерференционную картину. Направление распространения лучей 1 и 2 зависит от выбора конкретной оптической схемы. Например в опыте Ллойда луч 1 непосредственно падает на экран Э (рис.1), а луч 2 - отражается от зеркала. Так как интенсивности пучков 1 и 2 одинаковы и равны 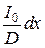(I₀ - интенсивность всего источника) распределение интенсивности в элементарной интерференционной картине будет следующим (см. соотношения (5) и (9) теоретического раздела):

, (2)

где D(x) - разность хода лучей 1 и 2 от данного элемента до точки наблюдения. Ее можно представить как:

, (3)

где D₀ - оптическая разность хода лучей a и b, вышедших из центра источника. Второе слагаемое в соотношении (3), дополнительная разность хода лучей 1 и 2 по отношению к лучам а и b, связано с конечным размером источника.

Найдем теперь распределение интенсивности в суммарной интерференционной картине:

, (4)

где .

Интегрируем (4):

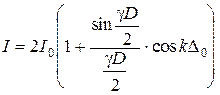. (5)

Видность интерференционных полос будет равна (рис.4):

Рис.4. Зависимость видности V от линейных D или угловых qразмеров источника

. (6)

Применим полученный результат к расчету видности интерференционной картины в схеме Юнга (рис.5):

, (7)

Рис.5 Интерференционная схема Юнга.

где d - расстояние между щелями, q - угловой размер источника света (щель ширины D).

Окончательно, видность V равна:

. (8)

Видность интерференционных полос, полученных от щелей S ₁ и S ₂ , равна нулю, если , т.е. при выполнении условия:

(9)

Если поместить щели S ₁ и S ₂ на расстоянии d > d _c, то видность интерференционных полос будет очень мала (см. рис.4; d > d _c, соответствует значениям аргумента ), т.е. колебания в точках S ₁ и S ₂ будут некогерентными. Другими словами, колебания в двух точках волнового фронта, отстоящих от источника света на расстоянии L, будут когерентными, если расстояние между ними не превосходит d _c. Эту величину называют радиусом (областью) когерентности.

Таким образом, оказывается, что интерференционный опыт Юнга позволяет выяснить, насколько когерентны между собой колебания в поперечном сечении светового пучка, достигающего щелей S ₁ и S ₂. Варьируя расстояние между щелями S ₁ и S ₂ и одновременно измеряя видность интерференционной картины на расположенном за ними экране, можно «обследовать» когерентность колебаний по всей площади этого сечения.

Уменьшение видности интереференционной картины, обусловленное конечным размером источника, связывают с понятием пространственной когерентности. А для количественной характеристики когерентности колебаний в поперечном сечении пучка вводят понятие радиуса когерентности.

Лазерная спекл - структура

Когда наблюдатель рассматривает в лазерном свете диффузно отражающий или преломляющий объект, изображение кажется ему зернистым. Создается впечатление, что поверхность объекта покрыта множеством мелких, хаотически расположенных светлых и темных пятнышек - так называемых спеклов (от английского слова speckle - испещрять). Если наблюдатель смещается, то ему кажется, что спекл - структура мерцает и смещается относительно объекта. Явление возникновения спеклов связано с использованием высококогерентного света.

Физическая природа спеклов проста. Каждая точка объекта рассеивает некоторое количество света в направлении наблюдателя. Вследствие своей высокой когерентности лазерный свет, рассеянный одной из точек объекта, интерферирует со светом, рассеянным любой другой точкой объекта. Сетчатка глаза регистрирует картину хаотической интерференционной картины. Это и есть спеклы. Хаотичность обусловлена шероховатостью поверхности, так как фаза рассеянного света изменяется случайно от точки к точке, следуя за вариациями высоты рельефа в данном месте. Аналогично можно рассмотреть и возникновение спеклов на экране при прохождении лазерного света через матовую пластинку.

Вследствие нерегулярной толщины матовой пластинки пространственно когерентная лазерная волна приобретает приращение фазы, случайным образом изменяющееся от точки к точке поверхности пластинки. Свет, прошедший через матовую пластинку, хорошо моделирует излучение протяженного самосветящегося источника.

Важное отличие матового стекла от самосветящегося источника света состоит в следующем: фазовые соотношения между световыми колебаниями в разных точках матового стекла нерегулярны, но неизменны во времени. Поэтому зернистая структура освещенности экрана также постоянна во времени. В случае же самосветящегося источника разность фаз колебаний в двух каких - либо точках его поверхности будет быстро изменяться, что приведет, очевидно, к хаотическому движению зерен и исчезновению зернистой структуры. Можно сказать, что спекл - картина, наблюдаемая от матового стекла, отвечает мгновенному распределению освещенности, возникающему в случае самосветящегося источника.

Участки экрана с повышенным значением освещенности отвечают, очевидно, тому, что волны, приходящие в них из различных точек матового стекла, оказываются, по случайным обстоятельствам, преимущественно синфазными. Наоборот, в участках с пониженной освещенностью происходит взаимное гашение волн, приходящих из различных точек матового стекла. Для того, чтобы степень синфазности этих волн существенно изменилась, нужно сместиться в плоскости экрана на некоторое расстояние; его среднее значение и будет определять размер области когерентности. Таким образом, «среднее зерно» есть область когерентности, а средний его размер - радиус когерентности.

При движении матового стекла происходит случайное изменение во времени фаз интерферирующих волн. Результирующее поле сходно со световым полем самосветящегося источника. При этом: радиус когерентности у полученного светового поля не изменяется (он определяется угловым размером источника), а спекл - картина исчезает.

Упражнение 1. Наблюдение и анализ лазерных спеклов.

Рис.6. Оптическая схема установки.

На рис.6 представлена оптическая схема установки. Здесь 1 - лазер, 2 - ко­роткофокусная линза, 3 - щель, 4 - матовое стекло, 5 - двойная щель, 6 -экран.

1. Включить лазер и добиться, чтобы лазерный луч распространялся вдоль оптической скамьи.

2. Установить на пути луча матовое стекло (МС). Получить на экране лазерные спеклы. Сдвигая экран, проследить за изменением размеров спеклов. Объяснить происходящие изменения.

3. Установить экран на конце оптической скамьи. Между лазером и МС поместить короткофокусную линзу. Сфокусировать лазерный пучок на матовом стекле. Пронаблюдать изменения размеров спеклов при перемещении линзы.

4. Убрать линзу, установить между лазером и МС щель. Плавно уменьшая ширину щели, проследить за изменением спеклов. Объяснить наблюдаемые изменения.

Упражнение 2. Определение радиуса когерентности светового поля.

Целью этого упражнения является проверка соотношения (9) и определение радиуса когерентности.

Если между источником света (ярким пятном на матовой пластинке) и экраном поместить двойную щель, то на экране будет наблюдаться интерференционная картина от этих щелей при условии, что расстояние между ними не превышает радиуса когерентности. Перемещая щель вдоль оптической скамьи (т.е. меняя угол q, см. рис.5), можно найти такое положение, при котором интерференционная картина исчезает. Это будет означать, что расстояние между щелями превысило радиус когерентности. Можно считать, что расстояние между щелями, при котором еще наблюдается интерференционная картина, соответствует радиусу когерентности.

1. Если зафиксировать расстояние между щелями и изменять размер источника (светящегося пятна на МС), то в соответствии с соотношением (9) должно изменяться расстояние от МС до двойной щели, при котором на экране исчезает интерференционная картина.

2. Между лазером и МС установить короткофокусную линзу (с фокусным расстоянием 6-8 см) и щель, с помощью которой можно будет изменять горизонтальный размер светящегося пятна на матовой пластинке. Рекомендуемые расстояния между оптическими элементами следующие: лазер-линза - 5-6 см, линза-щель - 17-20 см.

3. Открыть щель до 1.5 мм. Привести во вращение МС, включив тумблером питание электродвигателя.

4. Установить между МС и экраном двойную щель на расстоянии ~40 см от МС. Установить ширину двойной щели не более 0.3 мм. На экране должна появиться дифракционная картина от двух щелей: характерное чередование максимумов и минимумов.

5. Перемещая двойную щель вдоль оптической скамьи, найти положение, при котором дифракционная картина пропадает (моментом ее исчезновения считается исчезновение дифракционных минимумов по обе стороны от центрального максимума). Измерить расстояние L от МС до двойной щели. Размер источника D считать равным ширине щели, находящейся перед МС.

6. Уменьшая размер D светящегося пятна на МС с помощью первой щели с шагом 0.2 мм, определить несколько значений L по п.п. 4-5.

7. Построить график зависимости L от D. В соответствии с (9):

,

следовательно, по полученному графику можно определить радиус когерентности d_c. Длина волны излучения Не-Ne лазера l=632.8 нм.

 

Контрольные вопросы:

1. Интерференция монохроматического света. Расчет интерференционной картины при двухлучевой интерференции (оптический путь, оптическая разность хода, условия образования максимумов и минимумов, ширина интерференционной полосы).

2. Когерентные источники, способы их получения (метод деления амплитуды и метод деления волнового фронта).

3. Влияние размеров источников на видность интерференционной картины. Пространственная когерентность. Радиус когерентности.

4. Сформулируйте цель работы, опишите экспериментальную часть и обсудите результаты.

 

Дополнительная литература:

Демтредер В. Лазерная спектроскопия - М:, Наука, 1985.

Вест Ч. Голографическая интерферометрия - М:, Мир, 1982.

Лабораторная работа 26. Изучение зависимости показателя преломления газа от давления при помощи интерферометра Релея.

Согласно элементарной теории дисперсии показатель преломления n изотропной среды в области прозрачности связан с плотностью газа r соотношением Лоренц - Лорентца:

. (1)

Для газов, находящихся при невысоких давлениях, показатель преломления близок к единице. Поэтому уравнение (1) можно упростить:

или . (2)

При постоянной температуре плотность газа пропорциональна давлению P, следовательно:

. (3)

Из (3) можно получить соотношение, связывающее изменение показателя преломления газа d n с изменением давления d Р:

, (4)

где и - начальные значения показателя преломления и давления.

Таким образом, для газов, находящихся при невысоких давлениях, изменение показателя преломления линейно зависит от изменения давления.

В данной работе изучается зависимость показателя преломления воздуха от давления с помощью интерферометра Рэлея (ЛИР-1).

В интерферометре Рэлея интерференционная картина получается от двух когерентных световых пучков, прошедших через две параллельные щели.

Распределение интенсивности света I в зависимости от угла дифракции j при дифракции света на двух щелях, освещенных когерентным светом, показано наДифракция на каждой из широких щелей в отдельности дает для распределения интенсивности света I, дифрагировавшего по направлениям j, характерную дифракционную картину вида, изображенного рис. 1 сплошной линией.

Рис. 1. Распределение интенсивности в дифракционной картине отна двух параллельных щелей. ях шириной b - ширина одной щели,, расположенных на расстоянии d - расстояние между центрами щелей. Пунктирная кривая относится к случаю освещения щелей некогерентным светом.

Пунктирная кривая соответствовала бы сложению интенсивностей световых волн от обеих щелей, в том случае, если бы щели освещались некогерентным светом. Рисунок сделан в предположении, что d/b = 4.

Принципиальная схема интерферометра представлена на рис.2.

Лампа накаливания 1 с помощью линзы 2 освещает щель 3, расположенную в фокальной плоскости коллиматорной линзы 4.

Рис. 2. Оптическая схема интерферометра Рэлея: а - вид сбоку, б - вид сверху.

Параллельный пучок лучей, выходящих из коллиматорной линзы 4, разделяется двумя щелями 5. Эти щели (по принципу Гюйгенса) можно рассматривать как два источника вторичных световых волн. Так как прошедший через щели свет получен разделением фронта волны одного светового пучка, выходящего из одного источника света, то щели являются когерентными источниками света, а испускаемые ими световые волны - когерентными волнами.

Дифрагированные от этих щелей световые пучки проходят через объектив 7, причем, как видно из рис.2, верхняя часть пучков проходит через кюветы 6, а нижняя - непосредственно направляется в объектив 7. В результате в фокальной плоскости этого объектива происходит интерференция двух пар когерентных пучков. Первая пара, проходящая через кюветы, образует верхнюю систему интерференционных полос. Вторая пара, проходящая мимо кювет, образует нижнюю систему интерференционных полос. Интерференционные картины наблюдают с помощью цилиндрического окуляра 8 (стеклянной палочки) и глазной линзы 9. Целесообразность использования цилиндрической линзы состоит в том, что для удобства наблюдений требуется сильное увеличение интерференционной картины в направлении, перпендикулярном к узким и частым интерференционным полосам, получаемым в фокальной плоскости объектива 7 от широко расставленных щелей 5 (рис.2). Нужное увеличение дает цилиндрическая линза. В поле зрения окуляра 9 видны две системы интерференционных полос, расположенных одна под другой (рис.3).

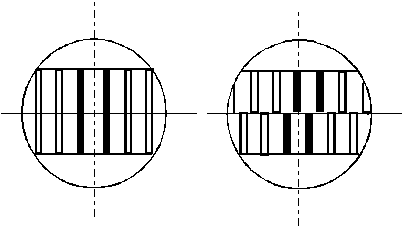а б Рис.3 Системы интерференционных полос, видимые в окуляр. а - при полной симметрии оптической системы; б - при заполнении кювет газами с различными показателями преломления.

При полной симметрии оптической системы и при одинаковых показателях преломления газов в обеих кюветах верхняя система полос совпадает с нижней (рис.3а).

Если заполнить кюветы интерферометра газами с разными показателями преломления, то у световых лучей, прошедших через кюветы, появится дополнительная разность хода , равная:

, (5)

где - длина кювет, , и - показатели преломления газов, и верхняя система полос сдвинется относительно нижней (рис.3б).

Отношение разности хода D к длине волны l называют порядком интерференции m. Число m:

(6)

может быть как целым, так и дробным. Очевидно, что по величине сдвига можно найти разность показателей преломления газов в кюветах.

В процессе измерений нижняя система интерференционных полос остается неподвижной и служит индикатором, по которому производится отсчет смещения верхней системы.

Сам метод измерений показателя преломления принадлежит к распространенному в физике классу компенсационных измерений. В интерферометре есть добавочное приспособление, состоящее из двух плоскопараллельных стеклянных пластинок 10 (рис.2). Эта пара наклонных пластинок образует компенсатор прибора. Он устроен следующим образом. Наклонно расположенные стеклянные пластинки пересекают верхние, проходящие через газовые кюветы световые пучки. Одна из пластинок неподвижна, а другая может вращаться вокруг горизонтальной оси, изменяя свой наклон (а значит и эффективную толщину) по отношению к проходящему сквозь нее световому пучку. Наклоняя пластинку, можно менять оптическую разность хода лучей, прошедших через кюветы и, в частности, сводить ее к нулю, если она создана неполной идентичностью изготовления кювет.

Подвижная пластинка компенсатора поворачивается с помощью рычага, приводимого в движение микрометрическим винтом 10 (рис.4).

Использование компенсатора для измерения показателя преломления заключается в следующем. Пусть обе газовые кюветы заполнены одинаковым газом, а видимые в окуляр интерференционные картины не точно совпадают друг с другом (за счет не идентичности кювет). Тогда с помощью микровинта с барабаном 10 (рис.4) можно привести верхнюю интерференционную картину к полному совпадению с нижней (индикаторной) картиной. Такому совпадению будет соответствовать некоторый отсчет на барабане микровинта. Этот отсчет в дальнейшем является нулевым отсчетом прибора.

Далее необходимо установить соответствие между отсчетами на барабане микровинта N_i, перемещавшего компенсатор, и величинойсмещения интерференционной картины.

Наличие нижней индикаторной картины делает удобным выражать это смещение в единицах порядка интерференции m. (см. соотношения (5 и 6)): при сдвиге интерференционной картины на одну полосу, m =1, на две полосы - m =2, и т.д. Результаты градуировки изображаются в виде графика, на котором по оси абсцисс откладываются отсчеты по барабану микровинта N_i, а по оси ординат - соответствующие им значения m..

При наличии градуировочного графика измерения на интерферометре сводятся к следующему. Оставляя неизменным давление в одной из кювет интерферометра, изменяют давление в другой кювете. Компенсируя для каждого давления получившийся сдвиг интерференционной картины и сопоставляя отсчеты на барабане с градуировочным графиком, находят по формулам (6) и (5).

Внешний вид установки представлен на рис.4.

Оптическая система прибора находится в цилиндрическом кожухе 7. Две идентичные кюветы 5 и 6 находятся в держателе внутри прибора. Кювета 5 открыта и является эталонной: давление в ней всегда равно атмосферному. Кювета 6, давление в которой меняется, соединена резиновым шлангом 4 с колбой 1. При помощи груши 3 можно увеличивать давление в колбе 1 и в кювете 6. Трехходовой кран 2 позволяет соединять кювету 6, колбу 1 и выход в атмосферу в различных комбинациях. Давление измеряется манометром 9, шкала которого проградуирована в мм. рт. ст.

 

Рис. 4. Внешний вид установки.

Интерференционная картина наблюдается в окуляр 11. В белом свете лампы накаливания центральная интерференционная полоса будет белой (ахроматичес­кая полоса), а полосы, расположенные справа и слева будут симметрично окрашенными. Совмещение верхней и нижней ахроматической полос производится поворотом компенсатора с помощью микрометрического винта 10.

Упражнение 1. Градуировка интерферометра.

Градуировка интерферометра в данной работе проводится для белого света, средняя длина волны которого l=550 нм, с кюветами, заполненными воздухом при атмосферном давлении.

1. Включить тумблер 12 «Сеть» (рис.4).

2. Определить нуль прибора. Для этого, вращая микрометрический винт, добиться того, чтобы верхняя ахроматическая полоса была продолжением нижней ахроматической полосы. Снять по барабану отсчет N₀ .

3. Сместить верхнюю интерференционную картину относительно нижней на одну полосу так, чтобы верхние светлые полосы снова совпали с нижними светлыми полосами (при этом m =1). Снять отсчет N ₁.

4. Сместить верхнюю интерференционную картину еще на одну полосу относительно нижней (m =2), снять отсчет N₂ и так повторять несколько раз, снимая отсчеты N_i по барабану микрометрического винта. Вращение барабана производить только в одну сторону.

5. Выключить прибор.

6. Построить график зависимости m от .

Упражнение 2. Определение зависимости показателя преломления воздуха от давления.

1. При помощи крана 2 установить в кювете 6 и колбе 1 (рис.4) атмосферное давление. Манометр должен показывать 0.

2. Включить тумблер 12 «Сеть» (рис.4).

3. Наблюдая интерференционную картину через окуляр, барабаном компенсатора привести систему верхних и нижних интерференционных полос к полному совмещению, как показано на рис. 3a. Снять по барабану отсчет .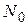

4. Не прекращая наблюдения в окуляр, осторожно нагнетать воздух при помощи груши 3 в кювету 6 (при этом кран 2 соединяет колбу 1 и трубку 6) до тех пор, пока верхняя система полос не сместится относительно нижней на 1 полосу. Закрыть кран 2.

5. Барабаном компенсатора снова привести системы полос к полному совпадению. Снять отсчеты по барабану компенсатора и по манометру. Найти и определить по градуировочному графику значения m, соответствующие 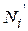. По формулам (5 и 6) определить , полагая нм.

6. Повышая давление в трубке 6, повторить измерения, описанные в пп 4 и 5. Таким образом получить несколько значений.

7. По полученным данным построить график зависимости от .

8. После окончания работы в трубке 6 и колбе 1 при помощи крана 2 установить атмосферное давление и выключить прибор.

Контрольные вопросы

1. Интерференция монохроматического света. Ширина интерференционных полос.

2. Способы получения когерентных пучков методом деления волнового фронта.

3. Связь показателя преломления с концентрацией. Формула Лоренц - Лорентца.

4. Устройство и принцип действия интерферометра Рэлея.

5. Сформулируйте цель работы, опишите экспериментальную часть и обсудите результаты.

Дополнительная литература:

Коломийцов Ю.В. Интерферометры - Л:, Машиностроение, 1976.

Физический практикум. Электричество и оптика под ред. В.И.Ивероновой.-М., «Наука», 1968.

 

Лабораторная работа 21. Определение длины световой волны при помощи бипризмы Френеля..................................................................................

Описание установки...................................................................

Упражнение................................................................................

Лабораторная работа 22. Определение радиуса кривизны линзы и длины световой волны с помощью колец Ньютона....................................

Описание установки...................................................................

Упражнение 1. Определение радиуса кривизны R сферической поверхности линзы......................

Упражнение 2. Определение длины волны максимума пропускания светофильтра......................

Упражнение 3. Определение спектральной ширины полосы пропускания.....................................

светофильтра............................................................................

Лабораторная работа 23. Микроинтерферометр Линника........

Описание прибора......................................................................

Упражнение 1. Определение глубины царапины.......................

Упражнение 2. Определение ширины полосы пропускания светофильтров

Лабораторная работа 24. Определение спектральных кривых пропускания интерференционных светофильтров..................................................

Описание установки...................................................................

Порядок выполнения работы....................................................

Лабораторная работа 25. Изучение пространственной когерентности монохроматических световых полей...............................................

Упражнение 1. Наблюдение и анализ лазерных спеклов.....................................................................

Упражнение 2. Определение радиуса когерентности светового поля...........................................

Лабораторная работа 26. Изучение зависимости показателя преломления газа от давления при помощи интерферометра Релея..............................

Упражнение 1. Градуировка интерферометра...............................................................................

Упражнение 2. Определение зависимости показателя преломления воздуха от давления...........

 

* Список обязательной литературы указывает преподаватель

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: