 |
Индивидуальные задания и отчет
|
|
|
|
Основы автоматизированного проектирования: Тема № 2
Построение и исследование математических моделей систем управления
Практика
Часть 1.
Оглавление
Объект исследования
Этап № 1. Описание функциональной схемы объекта
Этап № 2. Описание функциональных элементов и создание их субмоделей средствами пакета МВТУ
2.1.Уравнения, описывающие процессы в двигателе постоянного тока с независимым возбуждением
2.2. Описание параметров
2.3. Способы описания моделей и их реализация в пакете МВТУ
2.4. Создание отладочной модели № 1 (на базе структурной схемы)
Контрольные цифры
2.5. Создание отладочной модели № 2 (при представлении в виде системы дифференциальных уравнений в форме Коши и использовании блока типа «новый» в библиотеке «Динамические»)
2.6. Создание отладочной модели № 3 (при использовании блока типа «переменные состояния» в библиотеке «Динамические»)
3. Индивидуальные задания и отчет
Объект исследования: двигатель постоянного тока независимого возбуждения
Этап № 1. Описание функциональной схемы объекта
Выделяется единственный функциональный элемент:
- двигатель постоянного тока независимого возбуждения;
На рис. 1.1 приняты обозначения
qд, qд', qд"- угол поворота, скорость и ускорение вращения вала двигателя;
u - напряжение, приложенное к якорю двигателя;
Mв - возмущающий момент, на валу двигателя;
i я - ток в цепи якоря двигателя


Рис.1.1
Этап № 2. Описание функциональных элементов и создание их субмоделей средствами пакета МВТУ
2.1.Уравнения, описывающие процессы в двигателе постоянного тока с независимым возбуждением:
Ток в цепи якоря
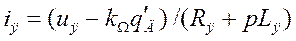 (1.1)
(1.1)
Момент, развиваемый на валу двигателя
|
|
|
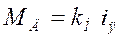 (1.2)
(1.2)
Ускорение поворота вала двигателя
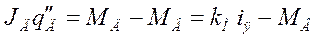 (1.3)
(1.3)
Здесь приняты обозначения
u д[В]- напряжение приложенное к якорю двигателя;
i я [А]- ток в цепи якоря двигателя;
q д [рад], q' д [рад/c]– угол и скорость поворота вала двигателя;
M д [Нм]– момент, развиваемый на валу двигателя;
M в[Нм]– возмущающий момент на валу двигателя;
k W=Umax/Wmax[Вс/рад]- коэффициент противо-ЭДС;
k м=1 /k д=Mд max/ i я max [Нм/А]– моментный коэффициент;
R я [Ом], L я [Гн] - сопротивление и индуктивность цепи якоря двигателя;
J д [кгм2]- момент инерции ротора двигателя.
При абсолютно жесткой механической передаче без люфта вместо момента инерции ротора двигателя следует рассматривать приведенный момент инерции J д+ J н/ i 2, где J н- момент инерции нагрузки, в этом случае передаточной функцией редуктора является интегрирующее звено с коэффициентом усиления равным обратной величине коэффициента передачи редуктора.
2.2. Описание параметров
В табл.1.1 приведены основные параметры, которые далее используются при построении модели двигателя.
Таблица № 1.1
| Имя в проекте | Переменная в описании | определение | тип |
| u | uд | Напряжение, приложенное к якорю двигателя | вход |
| Md | Mд | Момент двигателя | выход |
| Mв | Mв | Возмущающий момент, на валу двигателя | вход |
| q | qд | Угол поворота вала двигателя | выход |
| q'= pq | q'д | Скорость (частота) вращения вала двигателя | выход |
| i | iя | Ток в цепи якоря двигателя | выход |
| R | Rя | Сопротивление цепи якоря двигателя | глобальный параметр макроблока |
| L | Lя | Индуктивность цепи якоря двигателя | глобальный параметр макроблока |
| Jd | Jд (или J+Jн/i^2, где Jн- момент инерции нагрузки) | Момент инерции ротора двигателя (При абсолютно жесткой механической передаче без люфта вместо момента инерции ротора двигателя следует рассматривать приведенный момент инерции J+Jн/i^2, где Jн- момент инерции нагрузки). | глобальный параметр макроблока |
| km | kм | Моментный коэффициент; | глобальный параметр макроблока |
| kv | kW | коэффициент противо-ЭДС | глобальный параметр макроблока |
|
|
|
2.3. Способы описания моделей и их реализация в пакете МВТУ
Представление математической модели объекта возможно следующими способами:
- в виде структурной схемы, для получения которой используются известные преобразования по Лапласу;
- в виде системы дифференциальных уравнений;
- в матричной форме для системы линейных дифференциальных уравнений;
- в виде систем дифференциальных и алгебраических уравнений, логических элементов, табличных данных и.т.п.
- в общем виде, с использованием описания функционирования модели на языке программирования.
Для простого объекта в виде модели ДПТ, описываемой уравнениями (1.1-1.3) целесообразно использование первых трех форм описания с использованием типовых блоков пакета.
2.4. Создание отладочной модели № 1 (на базе структурной схемы)
Порядок действий
1. Создать отладочную схему (проект) следующего вида
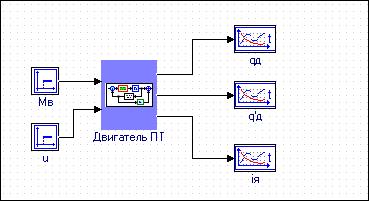
Рис.1.2
2. Двигатель постоянного тока описывается блоком «Макроблок» (см. библиотеку «Субструктуры»)
Вставив блок этого типа в новую схему, следует дать название блоку (см. рис. 1.2), сохранить его в файле с расширением и двойным щелчком открыть блок для заполнения его схемы
3. Нанести Порты входов и выходов модели в соответствии с рис. 1.3:
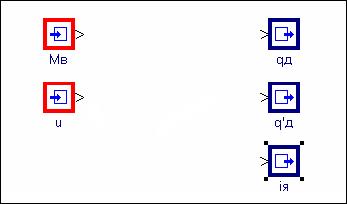
Рис.1.3
На рис. 1.3 показаны блоки Порты входа и Порты выхода (см. библиотеку «Субструктуры»)
4. Заполнить окно Глобальных параметров Проекта (субмодели) в соответствии с рис. 1.4:

Рис.1.4
5. Самостоятельно построить схему в соответствии с уравнениями для двигателя постоянного тока, используя идентификаторы параметров из таблицы № 1.1. Построение схемы основано на преобразованных по Лапласу уравнениях (1.1-1.3) и использовании типовых блоков пакета.
Далее предлагается один из способов представления модели.
1. Рассмотреть уравнение (1.1), преобразованное по Лапласу (далее для обозначения переменной Лапласа используем символ s). Оно имеет вид (1.4):
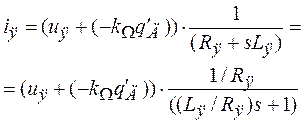 (1.4)
(1.4)
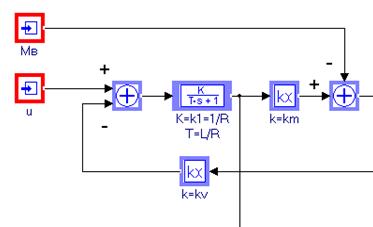
Очевидно, ему будет соответствовать схема с двумя последовательно соединенными блоками:
Весовой сумматор с двумя входами и коэффициентами усиления +1 и 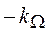 соответственно;
соответственно;
Апериодическое звено 1-го порядка 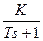 с коэффициентом усиления и постоянной времени
с коэффициентом усиления и постоянной времени 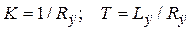 соответственно.
соответственно.
|
|
|
Фрагмент схемы приведен на рис. 1.5
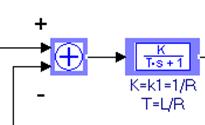
Рис. 1.5
Параметры блоков следующие:
коэффициенты Весового сумматора: 1 –kv;
коэффициент усиления и постоянная времени Звена 1 порядка: k1, T (расчет и описание параметров см.выше, рис.1.4).
В соответствии с общим подходом к составлению схемы входы и выходы блоков можно пока не соединять, однако целесообразно подписать сигналы входов-выходов. Для указанного фрагмента схемы входами будут напряжение u, которое является Портом входа (рис. 3) и сигнал угловой скорости вращения двигателя 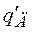 , пока не определенный, выходом будет ток якоря
, пока не определенный, выходом будет ток якоря 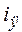 . Сигнал выхода используется не только для последующих блоков, но и как Порт выхода (см. рис.1.3).
. Сигнал выхода используется не только для последующих блоков, но и как Порт выхода (см. рис.1.3).
Модификация схемы ( для усиления наглядности ):
Блок Весовой сумматор имеет коэффициенты: +1 -1. Сигнал 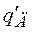 проходит через Усилитель с коэффициентом усиленияkv.
проходит через Усилитель с коэффициентом усиленияkv.
Фрагмент схемы в таком варианте представлен на рис. 1.6 (подключен сигнал с порта u).
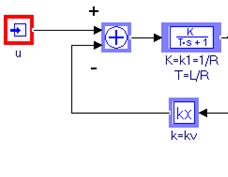 Рис.1.6
Рис.1.6
2. Рассмотреть уравнение момента, развиваемого на валу двигателя
(1.2), преобразованное по Лапласу:
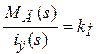
 (1.5)
(1.5)
Этому уравнению соответствует блок Усилитель с коэффициентом усиления 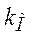 (идентификатор km).Так как входом является сигнал – ток якоря
(идентификатор km).Так как входом является сигнал – ток якоря 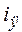 , очевидно, блок включается последовательно после Звена 1 порядка (см. п.1.). Выходом будет
, очевидно, блок включается последовательно после Звена 1 порядка (см. п.1.). Выходом будет 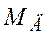 .
.
3. Для расчета правых частей уравнения (1.3) вычислить разность момента двигателя и возмущающего момента 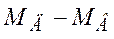 , для чего использовать Весовой сумматор с коэффициентами (+1 -1). Входами для блока будут сигнал с блока для расчета
, для чего использовать Весовой сумматор с коэффициентами (+1 -1). Входами для блока будут сигнал с блока для расчета 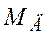 (см. п.2) и сигнал с Порта входа
(см. п.2) и сигнал с Порта входа 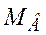
Фрагмент схемы теперь выглядит так:
4. В соответствии с уравнением (1.3), преобразованным к виду:
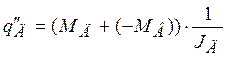 (1.6)
(1.6)
для получения углового ускорения 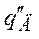 необходимо сигнал с выхода блока Сумматора (см.п.3) пропустить через Усилитель с коэффициентом усиления
необходимо сигнал с выхода блока Сумматора (см.п.3) пропустить через Усилитель с коэффициентом усиления 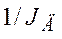 (идентификатор k2 - см. рис. 1.4).
(идентификатор k2 - см. рис. 1.4).
5. Для расчета угловой скорости 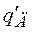 использовать блок Интегратор в соответствии с формулой преобразования по Лапласу:
использовать блок Интегратор в соответствии с формулой преобразования по Лапласу:
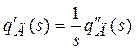 (1.7)
(1.7)
Входом будет сигнал с блока п.4, выходом – скорость 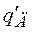 , которая используется и как Порт выхода (см. рис. 1.3), так и вход для блока Сумматора (усилителя) из п.1.
, которая используется и как Порт выхода (см. рис. 1.3), так и вход для блока Сумматора (усилителя) из п.1.
|
|
|
6. Для расчета угла поворота использовать аналогично блок Интегратор в соответствии с формулой преобразования по Лапласу:
 (1.8)
(1.8)
Выходной сигнал используется как Порт выхода (см. рис. 1.3).
7. Соединить между собой блоки в соответствии с указанными входами и выходами для каждого блока (не забыть подать сигналы на три порта выхода).
8. Провести моделирование отладочной схемы двигателя постоянного токаи сравнить с тестами рис.1.5 (приведено для Мв=1 на отрезке времени от 0 до 1 сек.)
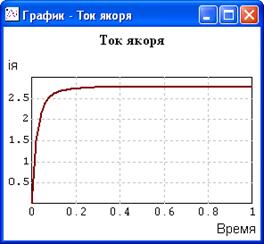
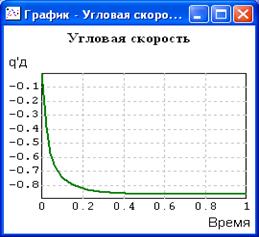
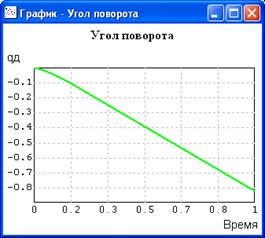
Контрольные цифры на 1 секунде
qд= -0.819234 q’д= -0.864189 iя= 2.77777
2.5. Создание отладочной модели № 2 (при представлении в виде системы дифференциальных уравнений в форме Коши и использовании блока типа «новый» в библиотеке «Динамические»)
Порядок действий
1. Привести исходную систему к нормальной форме Коши, т.е. так, чтобы она имела вид: 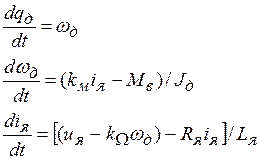
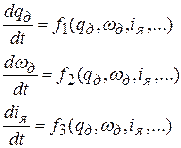 (1.9)
(1.9)
РЕКОМЕНДАЦИЯ:
Вводится новая переменная для обозначения угловой скорости поворота вала двигателя wД= q'д
Отсюда получается первое уравнение в форме Коши:
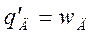 (1.10)
(1.10)
Второе уравнение получается из (1.6) после очевидной подстановки (1.10):
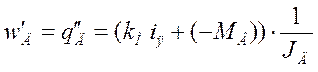 (1.11)
(1.11)
Третье уравнение берется из (1.4) после подстановки в него (1.10) и разрешения относительно выражения 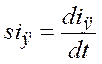
2. Запустить МВТУ и открыть проект с отладочной моделью № 1 (п.2.4 и рис.1.4) для субмодели двигателя постоянного тока
3. Скопировать блоки схемы (результат представлен на рис.1.6)
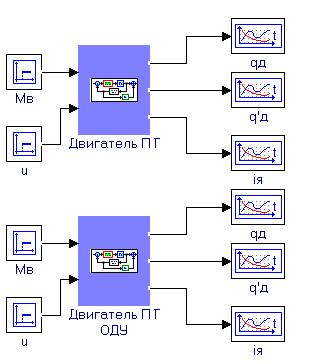
Рис.1.6.
4. Отредактировать 2-ую субмодель, расширив подпись под блоком («ОДУ») и заменив в ней структурную схему на блок типа «Новый» из библиотеки «Динамические»
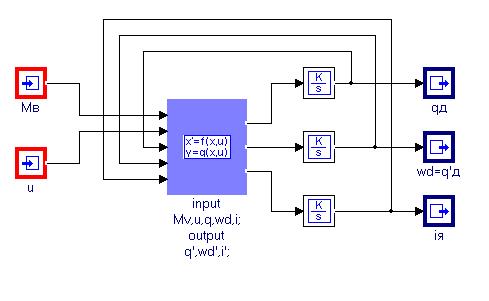
Рис.1.6.
Содержимое блока Новый
input Mv,u,q,wd,i;
q'=…;
wd'=…;
i'=…;
output q',wd',i';
Формулы дописать самостоятельно в соответствии с вышеописанными уравнениями: в правой части записываются выражения для производных.
Входами являются возмущающий момент и управляющий сигнал (напряжение) – как и ранее, кроме того, появляются дополнительные 3 входа – по числу переменных в системе дифференциальных уравнений (ключевое слово input). Производные этих переменных служат выходными сигналами (ключевое слово output)
РЕКОМЕНДАЦИЯ. При составлении системы дифференциальных уравнений рекомендуется рассчитывать внутри блока производные, подавать их на выход, а уже вне блока интегрировать систему с помощью блока «Интегратор» из библиотеки «Динамические».
Начальные условия интегратора соответствуют задаваемым для 3 неизвестных (в нашем случае берем все начальные условия нулевыми).
5. Провести моделирование. Результаты должны совпасть с отладочной моделью № 1
|
|
|
2.6. Создание отладочной модели № 3 (при использовании блока типа «переменные состояния» в библиотеке «Динамические»)
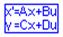 |
Порядок действий
1. Преобразовать систему в нормальной форме Коши из п.2.4, к представлению системы в пространстве состояний. Тогда она имеет вид
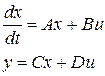 (1.12)
(1.12)
В нашем случае вектор независимых координат
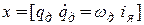 (1.13)
(1.13)
Вектор управляющих (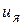 )и возмущающих (
)и возмущающих (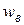 ) воздействий
) воздействий
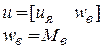 (1.14)
(1.14)
Преобразуем исходную систему, выделив в ней указанные компоненты.
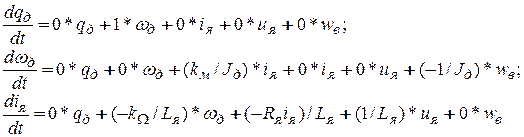 (1.15)
(1.15)
Выделив теперь коэффициенты при неизвестных и управляющих воздействиях, получим матрицы A,B
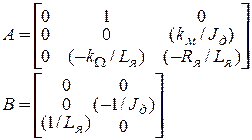 (1.16)
(1.16)
Предположив, что все координаты измеряемы (наблюдаемы), запишем также
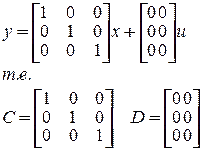 (1.17)
(1.17)
2. Скопировать схему из отладочной модели № 2 (п.2.4) – см. рис.1.6.
3. Сохранить ее под другим именем
4. 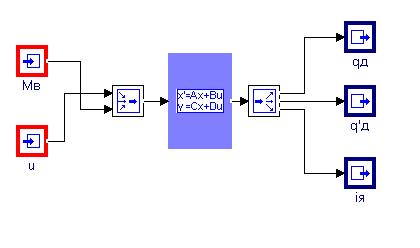 Отредактировать вторую субмодель двигателя (заменив блок типа «Новый» на блок «Переменные состояния» из той же библиотеки). Подпись под субмоделью изменить на «Двигатель ПТ:состояния». Содержимое новой субмодели представлено на рис. 1.7
Отредактировать вторую субмодель двигателя (заменив блок типа «Новый» на блок «Переменные состояния» из той же библиотеки). Подпись под субмоделью изменить на «Двигатель ПТ:состояния». Содержимое новой субмодели представлено на рис. 1.7
Рис.1.7.
5. В редакторе глобальных параметров сформировать матрицы A,B,C,D
Матрица А, при ее задании в диалоговом окне блока Переменные состояния, должна представляться как «особая» вектор-строка, содержащая элементы, каждый из которых является числовым вектором и содержит соответствующее число элементов (числовые или символьные значения соответствующего столбца матрицы А)
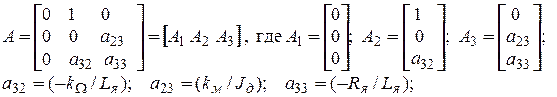
Аналогично представляются и другие матрицы, а именно
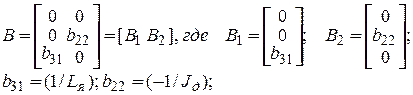
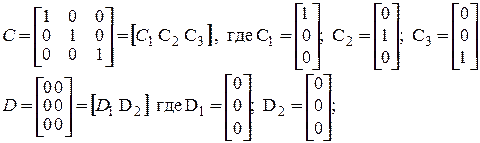
Анализ размерностей показывает, что:
число переменных состояний Nx=3;
число входных воздействий Nu=2;
число выходов Ny=3;
Вид окна глобальных параметров представлен на рис.1.8

Рис.1.8
6. Используя сформированные вектор - столбцы, следует заполнить параметры блока «Переменные состояния»
РЕКОМЕНДАЦИЯ.
Задаются
В 1-ой диалоговой строке – число переменных состояний Nx;
Во 2-ой диалоговой строке – число входных воздействий Nu;
В 3-ей диалоговой строке – число выходов Ny;
В 4-ой диалоговой строке – матрица системы А, [Nx*Nx];
В 5-ой диалоговой строке – матрица входа В, [Nu*Nx];
В 6-ой диалоговой строке – матрица выхода С, [Nx*Ny];
В 7-ой диалоговой строке – матрица обхода D, [Nu*Ny];
В 8-ой диалоговой строке – вектор начальных условий хi(0) при t = 0, [Nx].
Матрицы A, B, C и D задаются по СТОЛБЦАМ, а не по СТРОКАМ.
Каждый столбец записывается в КРУГЛЫХ скобках, внутри элементы отделяются друг от друга пробелами. С учетом использования обозначений для вектор - столбцов, заданных в Редакторе глобальных параметров, имеем, например, для матрицы A:
(A1)(A2)(A3)
Вектор начальных условий задается БЕЗ СКОБОК, через пробелы. В нашем случае: 0 0 0
7. Так как входы и выходы блока «Переменные состояния» должны быть векторными, следует дополнить схему модели двигателя блоками «Мультиплексор» и «Демультиплексор» соответственно (из библиотеки «Векторные»). На рис.1.7 показ вид субмодели, причем порядок входов «Мультиплексор» изменен в соответствии с порядком переменных в векторе управляющих воздействий (1.14).
8. Провести моделирование и убедиться в том, что все три варианта дают одинаковый результат (см. 1.5).
Индивидуальные задания и отчет
Создать модели объекта № 1 (двигателя постоянного тока) в пакете МВТУ с помощью следующих представлений математической модели:
- в виде структурной схемы, для получения которой используются известные преобразования по Лапласу (см. раздел 2.4);
- в виде системы дифференциальных уравнений в нормальной форме Коши (см. раздел 2.5);
- в матричной форме для системы линейных дифференциальных уравнений (представление в пространстве состояний – см. раздел 2.6);
Индивидуальными являются параметры двигателя, заданные в таблице 2 (см. также табл. 1.1):
| Вариант | R | L | Jd | km | kv |
| СМ7-61 | |||||
| Базовый | 0.5 | 0.01 | 0.04 | 0.36 | 0.45 |
| 0.2 | 0.1 | 0.02 | 0.008 | 0.072 | |
| 0.4 | 0.2 | 0.04 | 0.016 | 0.144 | |
| 0.6 | 0.3 | 0.06 | 0.024 | 0.216 | |
| 0.8 | 0.4 | 0.08 | 0.032 | 0.288 | |
| 1.2 | 0.6 | 0.12 | 0.048 | 0.432 | |
| 1.4 | 0.7 | 0.14 | 0.056 | 0.504 | |
| 1.6 | 0.8 | 0.16 | 0.064 | 0.576 | |
| 1.8 | 0.9 | 0.18 | 0.072 | 0.648 | |
| 0.2 | 0.08 | 0.72 | |||
| 2.2 | 1.1 | 0.22 | 0.088 | 0.792 | |
| 2.4 | 1.2 | 0.24 | 0.096 | 0.864 | |
| 2.6 | 1.3 | 0.26 | 0.104 | 0.936 | |
| 2.8 | 1.4 | 0.28 | 0.112 | 1.008 | |
| 1.5 | 0.3 | 0.12 | 1.08 | ||
| 3.2 | 1.6 | 0.32 | 0.128 | 1.152 | |
| 3.4 | 1.7 | 0.34 | 0.136 | 1.224 | |
| 3.6 | 1.6 | 0.32 | 0.128 | 1.152 | |
| 3.8 | 1.7 | 0.34 | 0.136 | 1.224 | |
| 4.0 | 1.8 | 0.35 | 0.138 | 1.152 | |
| 4.2 | 1.9 | 0.36 | 0.140 | 1.224 | |
| СМ7-62 | |||||
| 0.2 | 0.1 | 0.36 | 0.112 | 0.072 | |
| 0.4 | 0.2 | 0.38 | 0.12 | 0.144 | |
| 0.6 | 0.3 | 0.40 | 0.128 | 0.216 | |
| 0.8 | 0.4 | 0.42 | 0.136 | 0.288 | |
| 1.2 | 0.6 | 0.44 | 0.128 | 0.432 | |
| 1.4 | 0.7 | 0.46 | 0.136 | 0.504 | |
| 1.6 | 0.8 | 0.36 | 0.112 | 0.576 | |
| 1.8 | 0.9 | 0.38 | 0.12 | 0.648 | |
| 0.40 | 0.128 | 0.72 | |||
| 2.2 | 1.1 | 0.42 | 0.136 | 0.792 | |
| 2.4 | 1.2 | 0.44 | 0.128 | 0.864 | |
| 2.6 | 1.3 | 0.46 | 0.136 | 0.936 | |
В отчете должны содержаться:
1. Заголовок и Номер варианта
2. Содержимое блоков глобальных параметров для заданного варианта
3. Краткое описание представления модели (для КАЖДОГО из 3 представлений) и Рисунок схемы модели и субмоделей (если есть), содержимое блоков типа Новый или Переменные состояния (скопированы в документ WORD со схемы МВТУ через буфер обмена). Для копирования в буфер содержимого активного окна следует нажать одновременно клавиши ALT+Prt Scr. Описание дается для КАЖДОГО из 3 представлений.
4. Графики и контрольные цифры на 1 сек. для КАЖДОГО из 3 представлений.
|
|
|


