Каноническое уравнение гиперболы

Уравнение прямой на плоскости(параметрическое, каноническое и с угловым коэфф)

Уравнение с угловым коэффициентом.

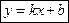
k= tg α – угловой коэффициент.

Если b=0 то прямая проходит через начало координат. Уравнение примет вид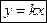

Если α=0, то k = tg α = 0. То прямая пройдет параллельно оси ох.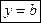

Если α=π/2, то уравнение теряет смысл. В этом случае уравнение примет вид и пройдет параллельно оси оу.

каноническое уравнение

Пусть N(x, y, z) — произвольная точка пространства. Построим вектор MN = {x − x0, y − y0, z − z0} (рис.1). 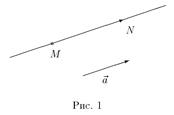Очевидно, что точка N принадлежит прямой тогда и только тогда, когда вектор MN коллинеарен вектору

когда их координаты пропорциональны:

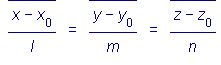Эти уравнения называются каноническими уравнениями прямой в пространстве.

параметрическое уравнение

Одна или две координаты направляющего вектора прямой →aмогут быть равны нулю, это означает, что числитель соответствующей дроби тоже равен нулю. Если в 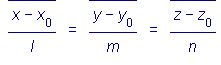ввести параметр t 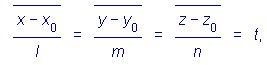то уравнения прямой можно записать в виде 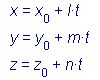Эти уравнения называются параметрическими уравнениями прямой.

 

Уравнение прямой на плоскости(с заданным нормальным вектором, общее уравнение и уравнение в отрезках на осях координат)

Общее уравнение прямой.

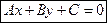
A, B, C – произвольные числа, причем А и В не равны нулю одновременно.

· Если В=0, то уравнение имеет вид или 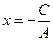. Это уравнение прямой, параллельной оси оу. и проходящей через точку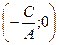

· Если В≠0, то получаем уравнение с угловым коэффициентом .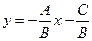

· Если А=0, то уравнение имеет вид 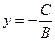. Это уравнение прямой, параллельной оси ох.

· Если С=0, то уравнение проходит через т. О (0;0).

Уравнение прямой в отрезках.

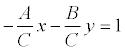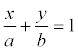Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим: или где 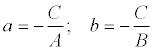Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.

с заданным нормальным вектором

Любой ненулевой вектор, перпендикулярный плоскости (прямой на плоскости) называется нормальным вектором этой плоскости (прямой на плоскости).

Теорема. Пусть 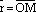радиус-вектор текущей точки М плоскости (прямой на плоскости), 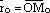– радиус- вектор какой-нибудь фиксированной точки 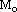плоскости (прямой на плоскости), 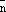– нормальный вектор плоскости (прямой на плоскости). Тогда уравнение 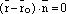является векторным уравнением плоскости (прямой на плоскости).

Нормированное уравнение прямой на плоскости. Расстояние от точки до плоскости.

Нормальное уравнение прямой.

Уравнение прямой можно записать в виде:

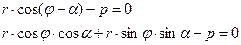
Т.к. 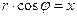; 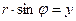, то:

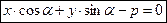
Расстояние от точки до плоскости.

Дано:

M₀ (x₀;y₀;z₀)

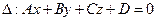
Расстояние d от точки М₀ до плоскости ∆ равно модулю проекции вектора 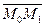(где М₁(x₁;y₁;z­₁) - произвольная точка плоскости) на направление нормального вектора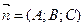

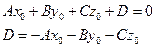
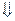
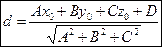
!!!Если плоскость задана уравнением:

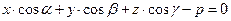
то расстояние до плоскости находится по формуле:

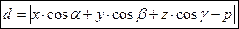
Взаимное расположение прямых на плоскости

На плоскости заданы прямые 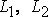общими уравнениями: Если выполнены условия 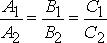то прямые 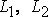совпадают Если выполнены условия то прямые 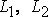параллельны

Векторы 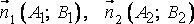- нормальные векторы прямых 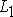и 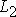соответственно. Если скалярное произведение векторов 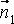и 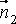обращается в ноль, т. е. то прямые 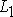и 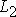перпендикулярны.

 

Условие перпендикулярности прямых 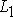и 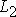в координатной форме:

Каноническое уравнение эллипса

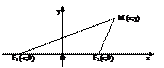Эллипсом называется

геометрическое место всех

точек плоскости, сумма

расстояний от которых до

до фокусов есть величина

постоянная, большая, чем расстояние между фокусами.

Пусть М (х;у) – произвольная точка эллипса.

Т.к. MF₁ + MF₂ = 2a

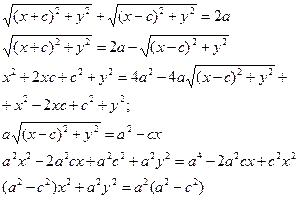
Т.к.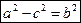

То получаем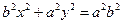

Или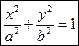

 

Каноническое уравнение гиперболы

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до фокусов есть величина постоянная.

Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF₁ – MF₂|=2a или MF₁ – MF₂=±2a,

 

 

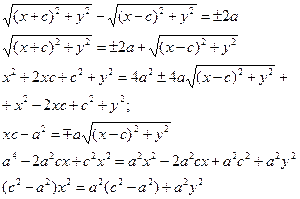
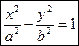
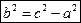
Поделиться:

Воспользуйтесь поиском по сайту: