Модуль «реальная математика»

14. Учёный Ива­нов вы­ез­жа­ет из Моск­вы на кон­фе­рен­цию в Санкт-Пе­тер­бург­ский уни­вер­си­тет. Ра­бо­та кон­фе­рен­ции на­чи­на­ет­ся в 10:00. В таб­ли­це дано рас­пи­са­ние ноч­ных по­ез­дов Москва — Санкт-Пе­тер­бург.

Номер по­ез­да	От­прав­ле­ние из Моск­вы	При­бы­тие в Санкт-Пе­тер­бург
026А	23:00	06:30
002А	23:55	07:55
038А	00:44	08:46
016А	01:00	08:38

Путь от вок­за­ла до уни­вер­си­те­та за­ни­ма­ет пол­то­ра часа. Ука­жи­те номер са­мо­го позд­не­го (по вре­ме­ни от­прав­ле­ния) из мос­ков­ских по­ез­дов, ко­то­рые под­хо­дят учёному Ива­но­ву.

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1) 026А 2) 002А 3) 038А 4) 016А

15. В таб­ли­це при­ве­де­ны ре­зуль­та­ты двух по­лу­фи­наль­ных за­бе­гов на ди­стан­цию 60 м. В фи­наль­ном за­бе­ге 6 участ­ни­ков. Из каж­до­го по­лу­фи­на­ла в финал вы­хо­дят два спортс­ме­на, по­ка­зав­ших пер­вый и вто­рой ре­зуль­та­ты. К ним до­бав­ля­ют еще двух спортс­ме­нов, по­ка­зав­ших луч­шее время среди всех осталь­ных участ­ни­ков по­лу­фи­на­лов.

За­пи­ши­те в ответ но­ме­ра спортс­ме­нов, не по­пав­ших в финал.

16. Спор­тив­ный ма­га­зин про­во­дит акцию: «Любая фут­бол­ка по цене 300 руб­лей. При по­куп­ке двух фут­бо­лок — скид­ка на вто­рую 60%». Сколь­ко руб­лей придётся за­пла­тить за по­куп­ку двух фут­бо­лок?

17. Маль­чик прошёл от дома по на­прав­ле­нию на во­сток 550 м. Затем по­вер­нул на север и прошёл 480 м. На каком рас­сто­я­нии (в мет­рах) от дома ока­зал­ся маль­чик?

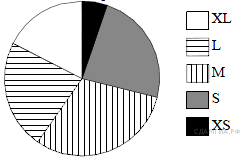
18. В ма­га­зи­не про­да­ют­ся фут­бол­ки пяти раз­ме­ров: XS, S, M, L и XL. Дан­ные по про­да­жам в июле пред­став­ле­ны на кру­го­вой диа­грам­ме. Какие утвер­жде­ния от­но­си­тель­но про­дан­ных в июле фут­бо­лок не­вер­ны, если всего в июле было про­да­но 180 таких фут­бо­лок? 1) Фут­бо­лок раз­ме­ра L было про­да­но более чем в три раза боль­ше, чем фут­бо­лок раз­ме­ра XS. 2) Фут­бо­лок раз­ме­ра S было про­да­но более 45 штук. 3) Боль­ше 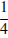всех про­дан­ных фут­бо­лок — фут­бол­ки раз­ме­ра M. 4) Боль­ше всего было про­да­но фут­бо­лок раз­ме­ра S.

19. Ве­ро­ят­ность того, что новая ша­ри­ко­вая ручка пишет плохо (или не пишет), равна 0,19. По­ку­па­тель в ма­га­зи­не вы­би­ра­ет одну такую ручку. Най­ди­те ве­ро­ят­ность того, что эта ручка пишет хо­ро­шо.

20. Чтобы пе­ре­ве­сти зна­че­ние тем­пе­ра­ту­ры по шкале Цель­сия (t ° C) в шкалу Фа­рен­гей­та (t ° F), поль­зу­ют­ся фор­му­лой F = 1,8 C + 32, где C — гра­ду­сы Цель­сия, F — гра­ду­сы Фа­рен­гей­та. Какая тем­пе­ра­ту­ра по шкале Цель­сия со­от­вет­ству­ет 63° по шкале Фа­рен­гей­та? Ответ округ­ли­те до де­ся­тых.

ЧАСТЬ 2

Модуль «АЛГЕБРА»

21 № 311546. Один из кор­ней урав­не­ния равен 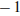. Най­ди­те вто­рой ко­рень.

22. Рас­сто­я­ние между го­ро­да­ми А и В равно 750 км. Из го­ро­да А в город В со ско­ро­стью 50 км/ч вы­ехал пер­вый ав­то­мо­биль, а через три часа после этого нав­стре­чу ему из го­ро­да В вы­ехал со ско­ро­стью 70 км/ч вто­рой ав­то­мо­биль. На каком рас­сто­я­нии от го­ро­да А ав­то­мо­би­ли встре­тят­ся?

23. По­строй­те гра­фик функ­ции 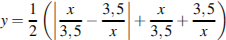и опре­де­ли­те, при каких зна­че­ни­ях пря­мая имеет с гра­фи­ком ровно одну общую точку.

Модуль «ГЕОМЕТРИЯ»

 

24. Окруж­ность с цен­тром на сто­ро­не AC тре­уголь­ни­ка ABC про­хо­дит через вер­ши­ну C и ка­са­ет­ся пря­мой AB в точке B. Най­ди­те диа­метр окруж­но­сти, если AB = 15, AC = 25.

 

25. В ост­ро­уголь­ном тре­уголь­ни­ке ABC точки A, C, центр опи­сан­ной окруж­но­сти O и точка пе­ре­се­че­ния высот H лежат на одной окруж­но­сти. До­ка­жи­те, что угол ABC равен 60°.

 

26. В тре­уголь­ни­ке 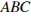угол 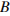равен 120°, а длина сто­ро­ны 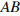на 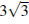мень­ше по­лу­пе­ри­мет­ра тре­уголь­ни­ка. Най­ди­те ра­ди­ус окруж­но­сти, ка­са­ю­щей­ся сто­ро­ны 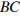и про­дол­же­ний сто­рон 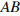и .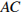

 

 

ВАРИАНТ 6

ЧАСТЬ 1

Модуль «АЛГЕБРА»

1. Най­ди­те зна­че­ние вы­ра­же­ния

2. На ко­ор­ди­нат­ной пря­мой от­ме­че­но число а.

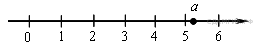
Какое из утвер­жде­ний от­но­си­тель­но этого числа яв­ля­ет­ся вер­ным?

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

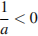1) 2) 3) 4)

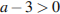
3. Най­ди­те зна­че­ние вы­ра­же­ния .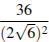

4. Решите уравнение Если кор­ней не­сколь­ко, за­пи­ши­те наибольший из них

5. Уста­но­ви­те со­от­вет­ствие между функ­ци­я­ми и их гра­фи­ка­ми.

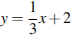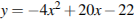А) Б) В)

 

 

За­пи­ши­те в ответ цифры, рас­по­ло­жив их в по­ряд­ке, со­от­вет­ству­ю­щем бук­вам:

А	Б	В

6. Ариф­ме­ти­че­ская про­грес­сия (a_n) за­да­на усло­ви­я­ми: a ₁ = 3, a_{n  + 1} = a_n + 4. Най­ди­те a ₁₀.

7. Най­ди­те зна­че­ние вы­ра­же­ния при , .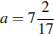

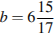8. Ре­ши­те не­ра­вен­ство 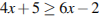и опре­де­ли­те, на каком ри­сун­ке изоб­ра­же­но мно­же­ство его ре­ше­ний.

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

Модуль «ГЕОМЕТРИЯ»

9. На про­дол­же­нии сто­ро­ны AD па­рал­ле­ло­грам­ма ABCD за точ­кой D от­ме­че­на точка E так, что DC = DE. Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма ABCD, если ∠DEC = 53°. Ответ дайте в гра­ду­сах.

 

10. От­ре­зок AB = 40 ка­са­ет­ся окруж­но­сти ра­ди­у­са 75 с цен­тром O в точке B. Окруж­ность пе­ре­се­ка­ет от­ре­зок AO в точке D. Най­ди­те AD.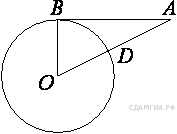

11. Одна из сто­рон па­рал­ле­ло­грам­ма равна 12, дру­гая равна 5, а синус од­но­го из углов равен 1/3. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма.

 

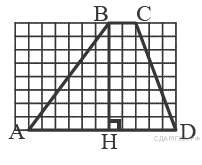
12. На ри­сун­ке изоб­ра­же­на тра­пе­ция 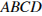. Ис­поль­зуя ри­су­нок, най­ди­те .

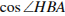13. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Бис­сек­три­са рав­но­бед­рен­но­го тре­уголь­ни­ка, про­ведённая из вер­ши­ны, про­ти­во­ле­жа­щей ос­но­ва­нию, делит ос­но­ва­ние на две рав­ные части.

2) В любом пря­мо­уголь­ни­ке диа­го­на­ли вза­им­но пер­пен­ди­ку­ляр­ны.

3) Для точки, ле­жа­щей на окруж­но­сти, рас­сто­я­ние до цен­тра окруж­но­сти равно ра­ди­у­су.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

⇐ Предыдущая123456Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: