 |
Формулы сокращенного умножения
|
|
|
|
Неравенство Коши
Пусть  и
и  неотрицательные числа, тогда
неотрицательные числа, тогда 
Формулы сокращенного умножения


1.1.МГУ 2017 (ДВИ) Что больше  или 3?
или 3?
1.2.МГУ 2017 (ДВИ) Что больше  или 3?
или 3?
1.3. МГУ 2017 (ДВИ) Что больше  или 3?
или 3?
1.4.МГУ 2017 (ДВИ) Что больше  или 3?
или 3?
Ответы: первое число больше
1.5.Ранхигс. Национальная экономика.
Даны три величины  . Выберите двойное неравенство, не выполняющееся ни при каком значении
. Выберите двойное неравенство, не выполняющееся ни при каком значении  :
:
1)  2)
2)  3)
3)  4)
4) 
Ответ 3)
1.6.Ранхигс. Национальная экономика.
Дана сумма четырех членов арифметической прогрессии 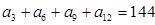 . Чему равна сумма первых 14 членов этой прогрессии?
. Чему равна сумма первых 14 членов этой прогрессии?
Ответ 504
1.7.В геометрической прогрессии первый, третий и пятый члены равны соответственно первому, четвертому и шестнадцатому члену некоторой арифметической прогрессии. Найдите пятый член арифметической прогрессии, если первый равен 5.
1.8.Ранхигс. Национальная экономика
Вычислите 
Ответ 8
1.9.ЕГЭ. Найдите значение выражения 
Ответ: 18
1.10. ЕГЭ. Найдите значение выражения 
Ответ: 3
1.11. ЕГЭ. Найдите значение выражения 
Ответ: -5
1.12. Найдите значение выражения 
Ответ: 4
1.13. Что больше  или
или  ?
?
1.14. Докажите что для любых положительных  и
и  выполнено
выполнено 
1.15. Докажите, что если  , то
, то 
1.16. Докажите, что если  , то
, то 
1.17. Докажите, что для любых действительных чисел  выполнено
выполнено 
Указание: представить а в виде суммы четырех выражений
1.18. Докажите, что если натуральное число  , то
, то 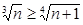
Указание: рассмотреть выражение 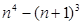
1.19. * Докажите что если  , то
, то 
1.20. Упростить выражение 
Ответ: 
1.21. ЕГЭ. Найдите  , если
, если 
1.22. Докажите что точный квадрат целого числа не может оканчиваться на 2,3,7,8 и нечетным количеством нулей
1.23. Ломоносов. Найти значение выражения

Ответ: 
1.24. Если  , то чему равно
, то чему равно  ?
?
1.25. Решить уравнение 
|
|
|
1.26. Ломоносов. Сумма 16054 натуральных чисел равна 2016*9, а их произведение  . Найдите все возможные наборы таких чисел. Укажите сумму наибольшего и наименьшего из чисел всех найденных наборов.
. Найдите все возможные наборы таких чисел. Укажите сумму наибольшего и наименьшего из чисел всех найденных наборов.
Ответ: 2020
1.27. Ломоносов. Найдите наибольшее n, для которого в десятиной записи «n» вместе с десятичной записью  используются все цифры от «1» до «9» ровно по одному разу («0» в набор не входит)
используются все цифры от «1» до «9» ровно по одному разу («0» в набор не входит)
Ответ: 854
1.28. Лицей Вторая школа
Что больше:  или
или  ?
?
1.29. Лицей Вторая школа
Докажите, что 
1.30. Пользуясь признаком делимости Паскаля, докажите делимость 19019 на 7
1.31. Докажите, что  делится на 440
делится на 440
1.32. Разложить на множители 
1.33. ЕГЭ. Укажите ближайшее целое число к

Указание: домножить и разделить на 
Ответ: 31
1.34. Решите в целых числах

Ответ: Решений нет
1.35. *ЕГЭ. В коробке находится 80 шаров нескольких цветов. Среди любых 13 взятых наугад окажется 4 шарика одного цвета. 1) обязательно ли среди шариков в коробке есть 20 шариков одного цвета? 2)Какое максимальное число шариков можно удалить из коробки, чтобы не испортить схему, но было 19 шариков одного цвета? 3)Какое минимальное количество шариков надо добавить, чтобы схема работала для 21 шарика?
1.36. ЕГЭ* На книжных полках 100 книг нескольких авторов. Среди любых 16 хотя бы четыре книги одного автора. Обязательно ли 1)20 книг одного автора? 2)21 книга одного автора?
2. Системы уравнений
Для решения системы уравнений, рассмотрим два различных подхода:
Первый: Уравнения системы линейны относительно неизвестных, тогда теорема Кронекера-Капелли отвечает на вопрос о множестве решений, а метод Гаусса эти решения находит. Если в задаче множество решений системы уравнений бесконечно, тогда для ее решения обычно используются свойства заданных неизвестных (например, тот факт что по условию неизвестные величины это натуральные числа или свойства положительности (отрицательности) или кратность заданных величин (то есть делимость без остатка на заданное по смыслу условия число)
|
|
|
Второй: Уравнения системы нелинейны относительно неизвестных, тогда, чаще всего нужно применить одну из формул сокращенного умножения 
2.1.Известно, что 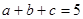 и
и  . Найдите
. Найдите 
2.2.Известно, что  и
и  . Найдите
. Найдите 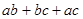
2.3.Известно, что  и
и  . Найдите
. Найдите 
2.4.Известно, что  и
и  . Найдите
. Найдите 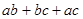
Ответы:
17, 10, 6, 15
2.5.ЕГЭ. Шариковая ручка стоит 10 рублей, гелиевая 50 рублей, перьевая 80 рублей. Сколько максимально можно купить гелиевых ручек, если всего ручек всех видов купить 20 штук и потратить на них 1000 рублей?
Ответ: 13
Схема кредитов и вкладов Ставка банка  измеряется в процентах и предполагает следующую схему:
измеряется в процентах и предполагает следующую схему:
1. Кредит. Банк отдает клиенту некоторую сумму (например 100 тысяч у.е.) на год и устанавливает ставку (например 18 % годовых), поэтому теперь клиент, взявший 100 тысяч, должен отдать за год 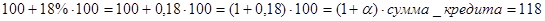 тысяч.
тысяч.
2. Вклад. Обратная схема. Клиент отдает банку некоторую сумму (например 100 тысяч у.е) на год и устанавливает ставку по вкладу (например 14 % годовых), поэтому теперь клиент, отдавший 100 тысяч должен получить за год  тысяч
тысяч
3. Итого: доход банка с двух пришедших клиентов равен 118-114 = 4 тысячи у.е.
Пример: 15-го января Вика планирует взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата следующие:
- 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число,
- выплата должна производиться один раз в месяц со 2-ого по 14-е число каждого месяца,
- 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей
| Дата | 15.01. | 15.02. | 15.03 | 15.04 | 15.05. | 15.06. | 15.07 |
| Долг В млн руб | 0,8 | 0,4 | 0,35 | 0,2 | 0,15 |
Найдите наибольшее значение r при котором Вике в общей сумме придется выплатить меньше 1,6 млн.
Решение: для того чтобы решить экономическую задачу нужно аккуратно составить математическую модель событий.
Шаг первый: Изначальное событие, Вика берет в Долг – 1 млн
Шаг второй: Что происходит после этого? Через две недели (как раз к 1 февраля) ее долг возрастает на r процентов, то есть теперь она должна 
Шаг третий: Вика выплачивает долг. Каким образом? Ну каким-то, сколько то она платит (естественно, ей выгодно поменьше платить, но! По условию договора, она должна платить, и платить так чтобы, осталось 0,8млн, поэтому ей видимо придется отдать банку  - 1 ый платеж
- 1 ый платеж
|
|
|
Шаг четвертый: Дальше ситуация повторится, с учетом того, что мы знаем о начисляемых процентах, и остатках на начало каждого месяца 
 - второй платеж,
- второй платеж,  - третий платеж,
- третий платеж,  - четвертый платеж,
- четвертый платеж, 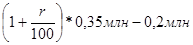 - пятый платеж,
- пятый платеж,  - шестой платеж и последний
- шестой платеж и последний  .
.
Шаг пятый: сложим вместе все платежи и вспомним, что нас просят по условию найти такое целое r, чтобы сумма всех платежей была  , тогда
, тогда 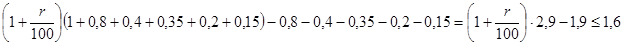 откуда
откуда  . Тогда наибольшим целым является r=20.
. Тогда наибольшим целым является r=20.
2.6.
Начало формы
Конец формы |
2.7.
|
2.8.ЕГЭ. Фермер получил кредит в банке под определенный процент годовых. Через год в счет погашения кредита вернул в банк 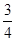 от всей суммы, которую он должен был банку к этому времени, а еще через год в счет полного погашения кредита он внес в банк сумму на
от всей суммы, которую он должен был банку к этому времени, а еще через год в счет полного погашения кредита он внес в банк сумму на  превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?
превышающую величину полученного кредита. Каков процент годовых по кредиту в данном банке?
|
|
|
2.9.ЕГЭ. 15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
- 1-ого числа каждого месяца долг возрастает на 2 процента по сравнению с концом предыдущего месяца,
-со 2ого по 14-ое число каждого месяца необходимо выплатить часть долга
-15ого числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-ое число предыдущего месяца.
Известно, что в течение второго года кредитования нужно вернуть банку 339 тыс.рублей. Какую сумму нужно вернуть банку в течение первого года кредитования?
Ответ: 411 тысяч
2.10. ЕГЭ. 15 января планируется взять кредит в банке на сумму 0,3 млн на 24 месяца. Условия его возврата таковы:
- 1-ого числа каждого месяца долг возрастает на 3 процента по сравнению с концом предыдущего месяца,
-со 2ого по 14-ое число каждого месяца необходимо выплатить часть долга
-15ого числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-ое число предыдущего месяца.
Какую сумму нужно вернуть банку в течение второго года кредитования?
Ответ: 179250 рублей
2.11. 1 января 2015 года Иван взял в банке 1 млн рублей в кредит. Схема выплаты кредита такая: 1-ого числа каждого следующего месяца банк начисляет 2 процента на оставшуюся сумму долга, затем Иван переводит платеж в банк. На какое минимальное количество месяцев Иван может взять кредит, чтобы ежемесячные выплаты были не более 200 тыс. рублей?
Ответ: 6
2.12. Матвей хочет взять кредит 1,4 млн рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть, последней) после начисления процентов. Ставка – 10 процентов годовых. На какое минимальное количество лет может Матвей взять кредит, чтобы ежегодные выплаты были не более 320 тысяч?
Ответ: 7
Метод интервалов
Решение неравенства, содержащих модуль, возможно с помощью таблицы интервалов.
Пример. 
Что делать? Чтобы раскрыть модули, нужно сначала внести данные в таблицу. Обратите внимание, сначала внешний модуль третьей дроби мы не трогаем, то есть во вложенных модулях раскрываем сначала внутренний модуль!

| 
| |

| + | + |

| - | + |
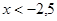
| - | - |
Теперь каждой строчке таблицы соответствует одно неравенство с одним модулем (внешний модуль третий дроби, который мы пока не раскрывали):
1. 

Модуль знаменателя третьей дроби разделяет неравенство на два различных случая:
а) 
тогда

б) 
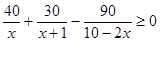
Каждое из неравенств решается обычным методом интервалов
2.  модуль третьей дроби раскрывается единственным способом
модуль третьей дроби раскрывается единственным способом

Рассмотрим теперь
3. 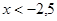

На интервале 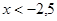 раскрытие возможно двумя способами
раскрытие возможно двумя способами
а) 

 :
:

Последнее неравенство представляет собой неравенство с дробью, в числителе и знаменателе которой отношение многочленов. Заметим, что знаменатель этой дроби является на интервале  неположительной величиной, а числитель положительной (проверьте, почему?), поэтому в целом представленное неравенство решений не имеет.
неположительной величиной, а числитель положительной (проверьте, почему?), поэтому в целом представленное неравенство решений не имеет.
|
|
|
2.13. ЕГЭ. Решить неравенство 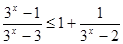
Ответ: 
2.14. ЕГЭ. Решите неравенство 
Ответ: 
2.15. ЕГЭ. Решите неравенство 
Ответ: 
3. Тригонометрия
Рассмотрим прямоугольную систему координат Оху. Введем на ней окружность радиуса 1 с началом в центре координат. Тогда уравнение этой окружности имеет вид 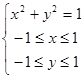
Назовем абсциссу х на этом круге косинусом, а ординату у – синусом.
Введем следующее соглашение: определим некоторый угол  , два луча которого изначально совпадают с осью абсцисс (угол АОА). Теперь один из лучей (луч ОА) начинает двигаться против часовой стрелки
, два луча которого изначально совпадают с осью абсцисс (угол АОА). Теперь один из лучей (луч ОА) начинает двигаться против часовой стрелки  . Точка с координатами (х,у) на этом круге движется вместе с лучом, начиная от точки А (1,0) против часовой стрелки и это направление считается положительным, либо по часовой стрелке и это направление считается отрицательным. Движение точки в оба направления бесконечно. Координаты точки на этом круге полностью определены величиной угла поворота. Таким образом, мы определили отображение множества углов поворота в два различных множества, абсцисс х и ординат у, то есть определили две функции
. Точка с координатами (х,у) на этом круге движется вместе с лучом, начиная от точки А (1,0) против часовой стрелки и это направление считается положительным, либо по часовой стрелке и это направление считается отрицательным. Движение точки в оба направления бесконечно. Координаты точки на этом круге полностью определены величиной угла поворота. Таким образом, мы определили отображение множества углов поворота в два различных множества, абсцисс х и ординат у, то есть определили две функции  и
и  . С учетом уравнения окружности получим выражение, называемое основным тригонометрическим тождеством
. С учетом уравнения окружности получим выражение, называемое основным тригонометрическим тождеством 

Рассмотрим два варианта измерения величины угла  .
.
Первый вариант: разделим полный круг на 360 одинаковых кусочков и назовем один кусочек – градус. Тогда половина круга (называемая развернутый угол) – 180 градусов. Четверть круга – 90 градусов. Очевидно 30 градусов – это одна третья часть от четверти круга, 45 градусов это половина четверти круга и т.д.
Второй вариант:Рассмотрим угол, полученный изначальным поворотом угла АОА ровно на сегмент круга равный 1 и назовем этот угол радианом. Раз мы рассматриваем окружность радиуса 1, то длина такой окружности =  , то есть полный поворот угла на 360 градусов соответствует углу в
, то есть полный поворот угла на 360 градусов соответствует углу в  радиан. Таким образом, мы ввели две системы измерения углов и установили соответствие между ними. Исходя из определения функции синус эта функция нечетная, а косинус функция четная.
радиан. Таким образом, мы ввели две системы измерения углов и установили соответствие между ними. Исходя из определения функции синус эта функция нечетная, а косинус функция четная.

Если вы забыли значение тригонометрической функции какого-то из стандартных углов запомните схему равностороннего треугольника со стороной 2:

В этом треугольнике синус угла  , как отношение противолежащего катета к гипотенузе равен
, как отношение противолежащего катета к гипотенузе равен  , поэтому
, поэтому  , аналогично:
, аналогично:

Угол  - это угол при биссектрисе, он равен
- это угол при биссектрисе, он равен  , аналогично для этого угла нашего треугольника:
, аналогично для этого угла нашего треугольника:

Группа 1:  Группа 2:
Группа 2: 
Из набора тригонометрических формул обычно доказывается одна, например косинус разности. Доказательство основано на применении понятия скалярного произведения для двух единичных векторов в координатах на тригонометрическом круге:

С учетом того, что на тригонометрическом круге вектора единичные и 

Функция  называется периодической, если существует такое
называется периодической, если существует такое 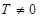 для которого выполняются два условия: 1) если
для которого выполняются два условия: 1) если  , то и
, то и 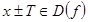 2) для любого
2) для любого  . Основным периодом периодической функции называется наименьший положительный период (если, конечно, он существует)
. Основным периодом периодической функции называется наименьший положительный период (если, конечно, он существует)
Основным периодом функций 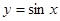 и
и  является
является  , а основным периодом
, а основным периодом  и
и  является
является 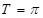
3.1.Сколько корней уравнения  расположено на отрезке
расположено на отрезке  ?
?
Ответ: 5
3.2.Найдите период функции  ?
?
Ответ: 
3.3.Лицей Вторая школа. Найдите периоды функции 
3.4.ЕГЭ. Найдите значение выражения 
3.5.ЕГЭ. Найти  , если
, если  и
и 
3.6.ЕГЭ. Найти  , если
, если 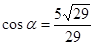 и
и 
3.7.ЕГЭ. Найти 
3.8.ЕГЭ. Решите уравнение  и найдите его корни, принадлежащие отрезку
и найдите его корни, принадлежащие отрезку 
Если тригонометрическое уравнение представляет собой линейную комбинацию синусов и косинусов различных выражений вида  ,
,  и
и  , выбираем из них пару, которая обладает следующим свойством:
, выбираем из них пару, которая обладает следующим свойством:  или
или  . Тогда к паре тригонометрических функций, содержащих
. Тогда к паре тригонометрических функций, содержащих  и
и 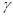 последовательным применением формул группы 1, уменьшаем аргументы тригонометрических функций.
последовательным применением формул группы 1, уменьшаем аргументы тригонометрических функций.
Для того чтобы решить тригонометрическое (ровно как и любое другое!) уравнение нам доступны два метода:
1. Сведем уравнение заменой переменного к квадратному, и решим его  если дискриминант отрицательный, то решений нет
если дискриминант отрицательный, то решений нет
2. Сведем уравнение к уравнению 
Пример. МГУ. ДВИ 2017
Решите уравнение 
"Методом пристального взгляда" видим, 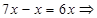 представим исходное уравнение в виде:
представим исходное уравнение в виде:
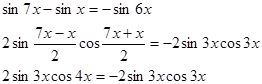
Теперь сократим уравнение на 2, и перенесем все слагаемые в одну сторону:

Применяя теперь формулу суммы косинусов, получим уравнение:
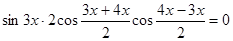 , теперь получим совокупность уравнений:
, теперь получим совокупность уравнений:



Множество решений третьего уравнения целиком входит во второе уравнение (почему? Докажите)
Ответ:  ,
, 
3.9.Решите уравнение 
Ответ 3.3. 
3.10. Решите уравнение 
Ответ 3.4. 
3.11. Решить уравнение 
Ответ 3.5. 
3.12. ЕГЭ. Решить уравнение и найти корни, принадлежащие интервалу 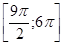

3.13. ЕГЭ. Решить уравнение  и найти корни, принадлежащие интервалу
и найти корни, принадлежащие интервалу 
3.14. ЕГЭ. Решите уравнение  и найти корни, принадлежащие интервалу
и найти корни, принадлежащие интервалу 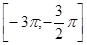
3.15. ЕГЭ. Решите уравнение  и найти корни, принадлежащие интервалу
и найти корни, принадлежащие интервалу 
3.16. ЕГЭ. Решите уравнение  и найти корни, принадлежащие интервалу
и найти корни, принадлежащие интервалу 
3.17. ЕГЭ. Решите уравнение 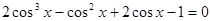 и найти корни, принадлежащие интервалу
и найти корни, принадлежащие интервалу 
3.18. ЕГЭ. Решите уравнение 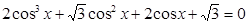 и найти корни, принадлежащие интервалу
и найти корни, принадлежащие интервалу 
3.19. ЕГЭ. Решите уравнение  и найти корни, принадлежащие интервалу
и найти корни, принадлежащие интервалу 
3.20. ЕГЭ. Решить уравнение  и найти корни, принадлежащие интервалу
и найти корни, принадлежащие интервалу 
3.21. ЕГЭ. Решить уравнение 
3.22. ЕГЭ. Решить уравнение 
3.23. ЕГЭ. Решить уравнение 
3.24. ЕГЭ. Решить уравнение  и найти его корни, принадлежащие интервалу
и найти его корни, принадлежащие интервалу 
3.25. Ларин. Решить уравнение 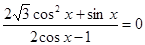 и найти его корни, принадлежащие отрезку
и найти его корни, принадлежащие отрезку 
Ответ:  ,
, 
3.26. Решить уравнение 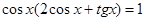 и найти его корни, принадлежащие отрезку
и найти его корни, принадлежащие отрезку 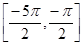
3.27. Найдите наибольший отрицательный корень уравнения 
Ответ: 
3.28. Найдите наибольший отрицательный корень уравнения 
3.29. Ларин. Известно, что  . Найдите
. Найдите 
3.30. Решить уравнение 
Вычисление тригонометрических выражений предполагает полет вашего воображения, потому что наш единственный шанс найти эту величину, это сведение к стандартным тригонометрическим углам.
Пример. Найти 
Наша цель: выразить число 18, как некоторую линейную комбинацию стандартных тригонометрических углов (то есть 30, 45, 60, 90 и т.д.) Например, так: 18 * 5 = 90, очевидно что 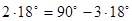
Обратите внимание, на следующее фундаментальное математическое утверждение: к алгебраическому равенству, не выходя за границы ОДЗ можно применить любую математическую функцию. Поэтому:

Теперь применяя формулы приведения получим:

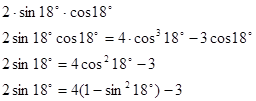
В результате заменой переменного  получим квадратное уравнение:
получим квадратное уравнение: 
 .
.  - положительная величина, так как 18 градусов принадлежит первой координатной четверти, отсюда
- положительная величина, так как 18 градусов принадлежит первой координатной четверти, отсюда
Ответ: 
3.31. Докажите таблицу значений тригонометрических функций нестандартных углов

| 
| 
| 
| 
| 
| 
| 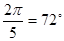
|

| 
| 
| 
| 
| 
| 
| 
|

| 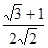
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 
| 
| 
| 
| 
|
3.32. Найти  , если известно
, если известно 
3.33. ЕГЭ. Найдите значение выражения 
3.34. ЕГЭ. Найдите значение выражения 
3.35. ЕГЭ. Найдите значение выражения 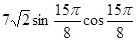
3.36. ЕГЭ. Найдите значение выражения 
Ответ: -4
3.37. Физтех, 2016. Найдите значение выражения 
3.38. МГУ, факультет почвоведения.
Найдите  и
и  , если известно, что
, если известно, что  и
и 
3.39. Вычислите 
3.40. Вычислить 
Указание: домножить на 
3.41. Вычислить 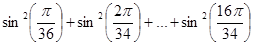
3.42. Ларин
А) Найдите значение выражения 
Б)Докажите, что 
В)Найдите значение выражения 
Ответ: а) 1 в) 
Экстремумы
Для определения наименьшего или наибольшего значения функции  на отрезке
на отрезке  , воспользуемся следствием из теоремы Ферма (если функция
, воспользуемся следствием из теоремы Ферма (если функция  дифференцируема на интервале
дифференцируема на интервале 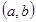 и принимает на нем наибольшее или наименьшее значение в точке
и принимает на нем наибольшее или наименьшее значение в точке  тогда производная в этой точке равна нулю
тогда производная в этой точке равна нулю  ). Тогда для нахождения наибольшего (наименьшего) значения достаточно проверить следующие факты: 1) функция дифференцируема на интервале (то есть нет разрывов и есть производная внутри интервала) 2) производная бывает равна нулю? Если нет, сразу проверяем значения функции на концах интервала (в точках а и б), определяем, где наибольшее и где наименьшее
). Тогда для нахождения наибольшего (наименьшего) значения достаточно проверить следующие факты: 1) функция дифференцируема на интервале (то есть нет разрывов и есть производная внутри интервала) 2) производная бывает равна нулю? Если нет, сразу проверяем значения функции на концах интервала (в точках а и б), определяем, где наибольшее и где наименьшее
3) производная равна нулю в некоторой точке, тогда если в этой точке знак производной поменялся с плюса на минус, в точке максимум, если с минуса на плюс, то минимум. Рекомендую запомнить внешний вид параболы (у которой всегда экстремум в вершине!)  - производная меняет знак с плюса на минус, значит в точке – максимум.
- производная меняет знак с плюса на минус, значит в точке – максимум.  - производная меняет знак с минуса на плюс, значит в вершине минимум.
- производная меняет знак с минуса на плюс, значит в вершине минимум.
3.43. ЕГЭ. Найдите наименьшее значение функции 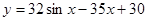 на отрезке
на отрезке 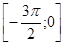
3.44. ЕГЭ. Найдите наименьшее значение функции  на отрезке
на отрезке 
3.45. ЕГЭ. Найдите наименьшее значение функции 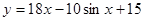 на отрезке
на отрезке 
3.46. ЕГЭ. Найдите точку минимума функции 
принадлежащую промежутку 
3.47. ЕГЭ. Найдите наименьшее значение функции 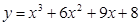 на отрезке
на отрезке 
3.48. ЕГЭ. Найдите наибольшее значение функции  на отрезке
на отрезке 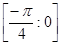
Ответ: 7
3.49. ЕГЭ. Найдите точку минимума функции 
Ответ: -10
3.50. ЕГЭ. Найдите наименьшее значение функции  на отрезке
на отрезке 
Ответ: 3
3.51. ЕГЭ. Най
|
|
|


