 |
Уравнение Д. Бернулли для элементарной струйки тока идеальной жидкости
|
|
|
|
Лекция 2. Одномерное движение несжимаемой жидкости
Учебные вопросы лекции
1. Основные понятия кинематики жидкости.
2. Уравнение Д.Бернулли для элементарной струйки тока идеальной жидкости.
3. Уравнение Д.Бернулли для одномерного потока реальной жидкости.
3. Истолкование уравнения Д.Бернулли. Его практическое применение.
4. Расход потока жидкости. Уравнение расхода (неразрывности). Измерение скорости потока и расхода жидкости.
1. Основные понятия кинематики жидкости
Кинематика жидкости – раздел гидромеханики, в котором изучаются виды и характеристики движения жидкости, но не рассматриваются силы, под действием которых это движение происходит [1].
Живым сечением ω называют площадь поперечного сечения потока, перпендикулярную к направлению течения.
Например, живое сечение трубы - круг (рис. 1, а); живое сечение клапана - кольцо с изменяющимся внутренним диаметром (рис. 1, б).
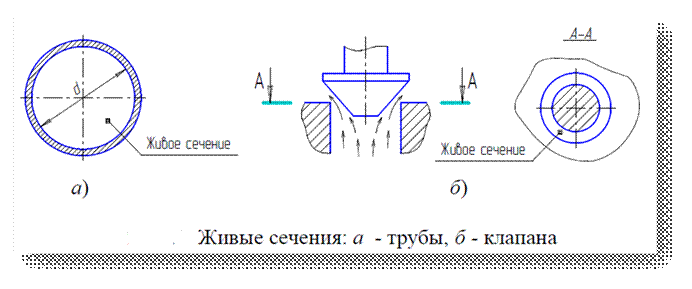 Рис. 1. Живые сечения: а - трубы, б - клапана
Рис. 1. Живые сечения: а - трубы, б - клапана
Смоченный периметр χ ("хи") - часть периметра живого сечения, ограниченное твердыми стенками (рис. 2), выделен утолщенной линией).

Рис. 2. Смоченный периметр
 Для круглой трубы:
Для круглой трубы:
 если угол в радианах,
если угол в радианах,
или:
Расход потока Q - объем жидкости V, протекающей за единицу времени t через живое сечение ω: 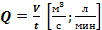
Средняя скорость потока υ - скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω:
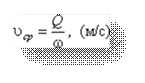
Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.
|
|
|
 Гидравлический радиус потока R - отношение живого сечения к смоченному периметру:
Гидравлический радиус потока R - отношение живого сечения к смоченному периметру:
Модель жидкости – совокупность жидких частиц, заполняющих объем без пустот и разрывов.
Жидкая частица – часть жидкости, малая по сравнению с объемом жидкости, но достаточно большая, чтобы пренебречь молекулярной структурой.
Полюс жидкой частицы – центр тяжести.
Объединяя закон сохранения вещества и условие постоянства расхода жидкости, можно сформулировать уравнение неразрывности течений.
Рассмотрим трубу с переменным живым сечением. Расход жидкости через нее в любом сечении постоянен:
Q1 = Q2 = const, тогда


Рис. 4. Иллюстрация к уравнению неразрывности
Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.
Трубка тока - трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока называется элементарной струйкой (рис. 5).
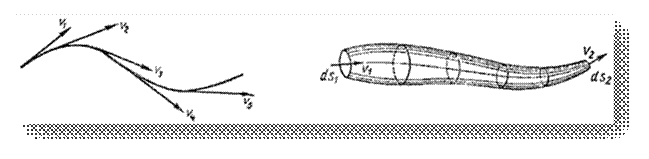
Рис. 5. Линия тока и струйка
Уравнение Д. Бернулли для элементарной струйки тока идеальной жидкости
Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости.
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис. 6).

Рис. 6. Схема к выводу уравнения Бернулли для идеальной жидкости
Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q. Для измерения давления жидкости применяют
|
|
|
пьезометры - тонкостенные стеклянные трубки, в которых жидкость поднимается на высоту 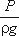 . В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.
. В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.
Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.
Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис. 6).
Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.
Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.
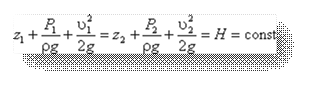 Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:
Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе: 
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.
С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:
z1 и z2 - удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;
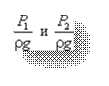 - удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
- удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
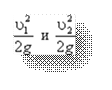
- удельные кинетические энергии в тех же сечениях.
Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.
Уравнение Бернулли можно истолковать и чисто геометрически.
Каждый член уравнения имеет линейную размерность. На рис. 6 видно, что
z1 и z2 - геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения;
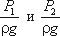 - пьезометрические высоты;
- пьезометрические высоты;
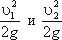 - скоростные высоты в указанных сечениях.
- скоростные высоты в указанных сечениях.
В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.
|
|
|
Литература
1. Лапшев Н. Н. Гидравлика. – М.: Изд-во «Академия/Academia», 2007 г. –272 с.
2. Кононов А.А., Кобзов Д.Ю., Кулаков Ю.Н., Ермашонок С.М. Основы гидравлики: Курс лекций. – Братск: ГОУВПО «БрГТУ». – 2004. – 92 с.
3. Ухин Б.В., Гусев А.А. Гидравлика. – М.: Изд-во ИНФРА-М, 2010 г. –432 с.
4. Малашкина В.А., Ушаков К.З. Гидравлика. – М.: Изд-во Горная книга, 2009 г. –414 с.
5.Башта Т.М., Руднев С.С., Некрасов Б.Б. и др. Гидравлика, гидромашины и гидроприводы. - М.: Машиностроение, 1982. -423 с.
6. Одномерный поток. Большая энциклопедия нефти и газа. URL: http://www.ngpedia.ru/id298931p1.html (дата обращения 06.02.2017 г.).
7. Скруббер Вентури. URL: https://ru.wikipedia.org/wiki/ (дата обращения 13.02.2017 г.).
8. Коагуляция. Словари и энциклопедии на Академике. URL: http://dic.academic.ru/dic.nsf/bse/163528/ (дата обращения 14.02.2017 г.).
9.Трубы для дымоходов. URL: http://stroy-banya.com/delaem_pech/deflektor-na-dymoxod.html (дата обращения 13.02.2017 г.).
10. Эффект земной подушки. URL: http://www.autocentre.ua/ac/ service/autofaq/effekt-zemnoy-podushki-233.html (дата обращения 25.01.2017).
11. Основы гидродинамики. URL: http://gidravl.narod.ru/osnovdin.html (дата обращения 25.01.2017).
|
|
|


