Практическая часть - решить две практические ситуации.

Ситуация 1

 

Рассматриваются два проекта А и Б относительно возможностей инвестирования. Известны прогнозные оценки значений дохода от каждого из этих проектов и соответствующие значения вероятностей.

Статистическим методом оценить степень риска каждого из этих проектов и выбрать один из них для инвестирования.

Мерой величины риска в статистическом методе признается колебание результатов.

Мерой колебания результатов некоторого ряда под влиянием разных факторов вероятности служит целая группа статистических величин: дисперсия, среднеквадратичное отклонение, коэффициент вариации.

Критерием выбора из нескольких инвестиционных проектов является минимум по всем основным статистическим параметрам.

 

	Прогнозируемая прибыль, тыс. грн.	Значения вероятностей
Проект А пессимистичная	800	0,4
Проект А сдержанная	1600	0,2
Проект А оптимистическая	2500	0,4
Проект Б пессимистичная	600	0,35
Проект Б сдержанная	1750	0,15
Проект Б оптимистическая	2450	0,5

 

Решение.

Найдем среднюю прибыль (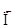) по проекту А и проекту Б.

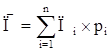, где

 

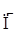- средняя прибыль;

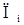- прибыль;

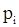 - вероятность получения прибыли.

 

= 800 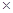0,4+1600 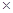0,2+2500 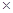0,4 = 320 + 320 + 1000 =1640 тыс.грн.

 

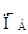= 600 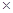0,35 + 1750 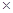0,15 + 2450 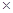0,5 = 210 + 262,5 + 1225 = 1697,5 тыс.грн.

 

Найдем дисперсию Д = 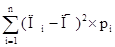                                     (1)

 

Д_А = (800-1640)² 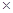0,4 + (1600-1640)²  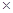0,2 + (2500-1640)² 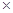0,4 = 543120

 

Найдем среднеквадратичное отклонение σ = 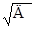                 (2)

 

σ_А =  = 760,52

 

Найдем коэффициент вариации ν = σ / 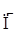                                         (3)

 

ν_А = 760,52 / 1640 = 0,46.

 

Найдем дисперсию Д_Б по формуле (1)

Д_Б = (600-1697,5)² 0,35 + (1750-1697,5)²  0,15 + (2450-1697,5)² 0,5 = 705118,8

 

Найдем среднеквадратичное отклонение σ_Б по формуле (2)

 

σ_Б = 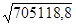 = 839,71

 

Найдем коэффициент вариации ν_Б по формуле (3)

 

ν_Б = 839,71 / 1697,5 = 0,49.

 

Критерием выбора из нескольких инвестиционных проектов является минимум по всем основным статистическим параметрам. Из двух проектов А и Б наименьшими показателями дисперсии, среднеквадратичного отклонения и коэффициента вариации обладает проект А. Следовательно, он обладает наименьшей степенью риска и выбирается для инвестирования.

 

Ситуация 2

 

При выборе рациональной стратегии производства (оптовых закупок в сфере товарного обращения) в условиях неопределенности и риска можно использовать игровые модели. Применение игровых моделей предлагается на примере компании, которая имеет несколько каналов сбыта продукции определенного ассортимента. Неопределенность в возможных колебаниях спроса на продукцию предприятия связана с тем, что:

- ежемесячный объем продукции со стойкими связями по сбыту на несколько лет в среднем составляет 489876,17 тыс. д. е. (низкая зависимость от изменений рыночной конъюнктуры);

- ежемесячный объем продукции со стойким сбытом, но не на продолжительный срок - 496324,33 тыс. д.е. (средняя зависимость от изменений конъюнктуры рынка);

- ежемесячный объем продукции обеспечен только разовыми закупками - 502772,5 тыс. д.е. (зависимость от изменений конъюнктуры высокая);

- ежемесячный объем продукции, покупатель на которую не определен - 478989,14 тыс. д. е. (зависимость от изменений конъюнктуры абсолютная).

Всего 1967962,1 тыс. д. е.

В розничной торговле с помощью этого примера можно определять объем оптовых закупок у поставщиков в зависимости от возможных колебаний платежеспособного спроса населения в районах реализации товара.

В задаче есть три стратегии производства продукции (закупок в сфере обращения):

 

S1 = 986200,50 тыс. д.е.

S2 = 1488973 тыс. д.е.

S3 = 1967962,1 тыс. д. е.

 

В зависимости от изменений рыночной конъюнктуры в связи с имеющимися возможностями реализации рассчитанные варианты среднегодовой прибыли, которые представлены в виде матрицы платежеспособного спроса, с учетом ожидаемого значения потерь в случае неудачного результата, связанных, например, с хранением нереализованной продукции, как следствие неиспользованных возможностей, нерационального распределения инвестиций, снижения оборотности оборотных средств, порчи или другими причинами. Значение матрицы определяются экспертным путем.

Ниже приводятся платежные матрицы по вариантам, каждый элемент которых является среднегодовой прибылью в результате выбора одной из трех стратегий производства (закупок) при разных состояниях рыночной конъюнктуры.

По условиям задачи требуется выбрать оптимальную стратегию производства (закупок). Для принятия решения в условиях неопределенности необходимо использовать:

"   критерий Лапласа;

"   максиминный критерий Вальда;

"   максимаксний критерий ("розового оптимизма");

"   критерий оптимизма Гурвица (λ =0,5);

"   критерий риска Севиджа.

Основываясь на полученных оценках выбрать оптимальную стратегию поведения предприятия на рынке.

 

Таблица №1. Зависимость прибыли предприятия от состояния рыночной коньюктуры и выбранной стратегии.

Стратегии	Состояние рыночной коньюктуры
	1	2	3	4
S1 = 986200,50 тыс. д.е.	5 931,03	29 724,10	29 724,10	29 724,10
S2 = 1488973 тыс. д.е.	-7,00	24 889,30	39 779,60	39 779,60
S3 = 1967962,1 тыс.д.е.	-214,00	10 839,11	29 679,21	49 359,42

 

Решение

Выберем оптимальную стратегию производства. Для принятия решения в условиях неопределенности поочередно используем:

1. критерий Лапласа;

2. максиминный критерий Вальда;

3. максимаксний критерий ("розового оптимизма");

4. критерий оптимизма Гурвица (λ =0,5);

5. критерий риска Севиджа.

1. Рассчитаем оптимальную стратегию, используя критерий Лапласа.

Критерий Лапласа определяется по формуле:

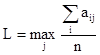, в нашем случае n =4,  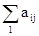= 95103,3, 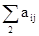= 104441,5,

 

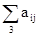 = 199544,8

 

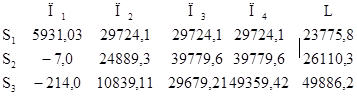
Наибольшее значение критерия Лапласа получаем при стратегии S₃. Стратегия S₃ –оптимальна.

2. Рассчитаем оптимальную стратегию, используя максиминный критерий Вальда.

Критерий Вальда определяется по формуле:

 

 

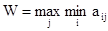
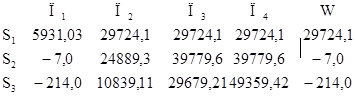
Максимальное значение критерия Вальда получаем при первой стратегии S₁. Стратегия S₁ –оптимальна.

3. Рассчитаем оптимальную стратегию, используя максимаксний критерий ("розового оптимизма").

Максимаксний критерий определяется по формуле:

 

 

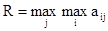
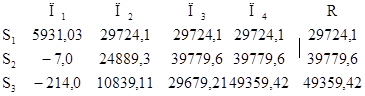
Максимальное значение максимаксного критерия получаем при третьей стратегии S₃. Стратегия S₃ –оптимальна.

4. Рассчитаем оптимальную стратегию, используя критерий оптимизма Гурвица.

Критерий Гурвица определяется по формуле:

 

,

 

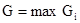
В нашем примере λ = 0,5 и Формула для определения критерия Гурвица сводится к формуле

 

.

 

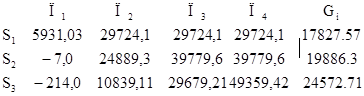
Максимальное значение критерия Гурвица получаем при третьей стратегии S₃. Стратегия S₃ –оптимальна.

5. Рассчитаем оптимальную стратегию, используя критерий риска Севиджа.

Для определения критерия Севиджа составим матрицу рисков на основе платежной матрицы. Для определения значений матрицы рисков используем следующую формулу:

 

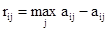
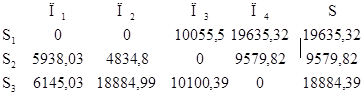
Значение критерия Севиджа определим по формуле:

 

 

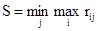
Минимальное значение критерия Севиджа получаем при второй стратегии S₂. Стратегия S₂ –оптимальна.

Итак, подведем итоги:

1. критерий Лапласа - оптимальна стратегия S₃;

2. максиминный критерий Вальда - оптимальна стратегия S₁;

3. максимаксний критерий ("розового оптимизма") - оптимальна стратегия S₃;

4. критерий оптимизма Гурвица - оптимальна стратегия S₃;

5. критерий риска Севиджа - оптимальна стратегия S₂.

Наиболее часто условие оптимальности выполняется при третьей стратегии S₃. Следовательно, выбираем третью стратегию, в соответствии с которой производится продукции на 1967962,1 тыс.д.е.

Литература

 

1. Івченко И.Ю. Экономические риски: Учебное пособие. - К.: "Центр учебной литературы", 2004. - 304 с.

2. Балабанов И.Т. Риск-менеджмент. - Г.: Финансы и статистика, 1998.

3. Лапуста М.Г. Риски в предпринимательской деятельности. -Г.: 1997.

4. Чернов В.А. Анализ коммерческого черточка. Г. - 1998.

5. Г.Б. Клейнер, В.Л. Тамбовцев, Р.М. Качалов. Предприятие в нестабильной экономической среде: риски, стратегии, безопасность.- Г.: 1995.

6. Оценка инновационного риска http://www.risk-manage.ru/research/

12	Поделиться:

Воспользуйтесь поиском по сайту: