Главная | Обратная связь | Поможем написать вашу работу!

I. Изучение распада нейтральных частиц

Стр 1 из 2Следующая ⇒

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Кафедра «Физика-2»

С.М. Кокин, С.В. Мухин

ФИЗИКА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНЫМ РАБОТАМ 48, 66, 67, 148

МОСКВА - 2007

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ (МИИТ)

Кафедра «Физика-2»

С.М. Кокин, С.В. Мухин

ФИЗИКА

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ЛАБОРАТОРНЫМ РАБОТАМ 48, 66, 67, 148

Рекомендовано редакционно-издательским советом университета

в качестве методических указаний для студентов специальностей

ИУИТ, ИСУТЭ, ИЭФ, ИТТОП, ИКБ, вечернего факультета

МОСКВА - 2007

УДК 535

K-59

Кокин С.М., Мухин С.В. Физика. Методические указания к лабораторным работам 48, 66, 67, 148. – М.: МИИТ, 2007. – 46 с.

Методические указания содержат описания лабораторных работ по общему курсу физики, предназначенных для студентов первого и второго курсов институтов ИУИТ. ИСУТЭ, ИТТОП, ИЭФ, ИКБ, вечернего факультета.

Авторы:	профессор С.М. Кокин – работы 48, 66, 67, 148
старший преподаватель С.В. Мухин – работы 66, 67
Работа 48 в МИИТе впервые поставлена проф. Е.И. Тимошкиным, работы 66, 67 – доц. Н.П. Наровской.

университет путей сообщения

(МИИТ), 2007

Работа 48

ОПЫТ ФРАНКА И ГЕРЦА

Цель работы: подтверждение боровской теории строения водородоподобных атомов

Приборы и принадлежности: Электронная лампа-тиратрон с трансформатором, звуковой генератор, электронный осциллограф.

Введение

В истории создания современной теории строения атома важное значение имели опыты по рассеянию альфа-частиц тонкими металлическими фольгами, на основе которых Резерфордом была предложена планетарная модель атома. Однако классическая теория этой модели оказалась не в состоянии объяснить установленные к тому времени закономерности излучения атомов. Выход из создавшегося затруднения был предложен Бором, отказавшимся от применения к атому законов классической электродинамики.

Опираясь на идею о квантах, высказанную Планком при объяснении закономерностей теплового излучения, Бор развил квантовую теорию строения атома, которая применима к атому водорода и к так называемой водородоподобной системе, состоящей из ядра с зарядом Ze и одного электрона, вращающегося вокруг ядра. Такую систему называют также изоэлектронной водороду. Примерами подобных систем являются ионы Не⁺, Li⁺⁺ и др.

В основе теории Бора лежат следующие постулаты.

Первый постулат Бора (постулат стационарных состояний): существуют некоторые стационарные состояния атома, находясь в которых он не излучает энергии. В этих состояниях атомные системы обладают энергиями, образующими дискретный ряд: E ₁, E ₂,..., Е _n. Такие состояния характеризуются устойчивостью; всякое изменение энергии в результате поглощения или испускания электромагнитного излучения (а также в результате соударения) может происходить только при скачкообразном переходе системы из одного состояния в другое.

Второй постулат Бора (правило частот) устанавливает, что при переходе атома из одного стационарного состояния в другое испускается или поглощается один фотон. Излучение происходит при переходе атома из состояния с большей энергией в состояние с меньшей энергией (при переходе электрона с орбиты, удаленной от ядра, на более близкую к ядру орбиту). Напротив, поглощение фотона сопровождается переходом атома в состояние с большей энергией. Этому соответствует переход электрона на более удаленную от ядра орбиту. Изменение энергии атома, связанное с излучением или поглощением фотона, пропорционально частоте ν. Если D E – изменение энергии атома в результате этих процессов, то

D E = h ν. (1)

Правило частот Бора может быть записано иначе. Если Е _n и Е _m– энергия атома в двух стационарных состояниях с номерами n и m соответственно, то

Е _n – Е _m = h ν _mn. (2)

При Е _m < Е _n происходит излучение фотона, при Е _m > Е _n – его поглощение.

Третий постулат Бора (правило квантования орбит) утверждает, что в стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь квантованные значения момента импульса, удовлетворяющие условию

L _n = mur = nh /(2p), где n = 1; 2; 3; (3)

Здесь m – масса, u – скорость электрона, r – радиус его орбиты, h = 6,62×10^-³⁴ Дж×с – постоянная Планка*.

Постулаты Бора резко противоречат требованиям классической электродинамики. Так, например, по первому постулату атомы не излучают энергию, несмотря на то, что входящие в атомы электроны движутся с ускорением (центростремительным), частоты фотонов ν, испускаемых атомами, согласно третьему постулату не имеют ничего общего с частотами обращения электронов вокруг ядер, а второй постулат вообще невозможно интерпретировать в рамках классической физики.

Постулаты Бора нашли непосредственное подтверждение в опытах Франка и Герца по изучению столкновений электронов, ускоряемых электрическим полем, с атомами инертных газов и паров металлов. Эти элементы использовались потому, что их атомы не проявляют склонности к захвату электронов и образованию отрицательных ионов.

В опытах Франка и Герца было обнаружено, что электроны могут испытывать с атомами столкновения двух типов:

– упругие столкновения, при которых электрон отскакивает от атома без потери энергии и лишь меняет направление движения;

– неупругие столкновения, при которых электрон отдает большую часть своей кинетической энергии (или даже всю энергию) атому, и, следовательно, резко уменьшает свою скорость; при этом атом переходит в возбужденное состояние.

Упругие столкновения имеют место, когда кинетическая энергия электронов меньше разности энергий основного Е (n = 1) и первого возбужденного состояния Е (n = 2) атома: в этом случае электроны практически не передают атомам энергии. Если же кинетическая энергия электронов становится равной Е (n = 2) – Е (n = 1), то электроны испытывают неупругие столкновения, в результате которых атом переходит в первое возбужденное состояние.

Из этого состояния атом через некоторое, очень короткое время (около 10^-⁷с), переходит в основное состояние, испуская фотон с энергией h ν₁ = Е (n = 2) – Е (n = 1), совпадающей с энергией eU ₁, которой обладал электрон перед неупругим столкновением с атомом. В соответствии с этим потенциал U ₁называется первым критическим потенциалом возбуждения, или резонансным потенциалом, а частота ν ₁ – резонансной частотой.

Если электронам сообщить достаточно большую энергию, то при неупругих столкновениях они могут перевести атом во второе (n = 3), третье (n = 4) и более высокие возбужденные состояния с энергиями, соответствующими более высоким энергетическим уровням атома. При этом выполняются соотношения:

Е (n = 3) - Е (n = 1) = еU _II = h ν_II; Е (n = 4) - Е (n = 1) = еU _III = hν _III и т. д.

Соответственно потенциал U _II называется вторым потенциалом возбуждения, U _III – третьим потенциалом возбуждения и т. д.

Таким образом, атом либо вообще не поглощает энергию (испытывая упругое соударение с электроном), либо поглощает ее, но в количестве, равном разности энергий двух стационарных состояний.

Опыты Франка и Герца послужили непосредственным обоснованием постулатов Бора о дискретности стационарных состояний атомов. Они позволили установить для ряда атомов значения энергии, необходимые для перевода атома из одного устойчивого состояния в другое. Полученные из этих опытов длины волн излучения некоторых газов, приводимые в табл. 1, с большой степенью точности совпадают с данными спектроскопических измерений.

Таблица 1

Элемент	Гелий	Неон	Ксенон	Криптон
Длина волны, нм	62,5 60,3	74,3 58,5	147,0 109,8	123,6 87,8

Метод измерения и описание аппаратуры

Определение второго, третьего и следующих потенциалов возбуждения представляет значительную экспериментальную трудность и требует применения специальной аппаратуры. Первый же, резонансный потенциал можно определить с помощью простого устройства, представляющего собой трёхэлектродную лампу, заполненную парами металла или инертным газом. Для доказательства существования неупругих соударений и определения значения потенциала, при котором они наблюдаются, удобно использовать метод задерживающего поля. Электрическая схема соответствующей установки представлена на рис. 1.

Электроны, испускаемые накалённым катодом К, ускоряются электрическим полем между катодом и сеткой С и направляются к аноду А, который в данном случае является собирающим электродом (коллектором). Между сеткой и коллектором создаётся слабое тормозящее поле. Поэтому только те электроны, которые обладают кинетической энергией, достаточной для преодоления тормозящего поля, достигнут коллектора и создадут ток, регистрируемый гальванометром Г. Если постепенно увеличивать ускоряющий потенциал с помощью потенциометра П и одновременно измерять ток с помощью гальванометра, то в результате получается вольт-амперная характеристика, изображенная на рис. 2.

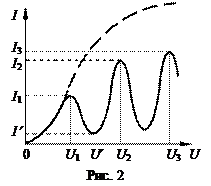Начальный участок этой характеристики имеет вид, обычный для вольт-амперных характеристик термоэлектронных приборов. Но при потенциале U ₁ ток внезапно резко падает, а затем вновь начинает возрастать до потенциала U ₂, при котором вновь обнаруживается резкое падение тока и новое его возрастание до потенциала U ₃. Так, например, в случае, если опыт проводится в парах ртути, то тогда оказывается, что U ₁ = 4,1 В; U ₂ = 9,0 В и U ₃ = 13,9 В. Таким образом, вся кривая представляет собой ряд острых максимумов, отстоящих друг от друга на расстоянии, соответствующем 4,9 В.

Истолкование максимумов на вольт-амперной характеристике не представляет особых затруднений. До тех пор, пока энергия электрона не достигает eU ₁, он испытывает с атомами газа упругие соударения, и ток возрастает с увеличением потенциала по обычному закону. При потенциале U ₁ удар становится неупругим, электрон отдает при соударении атому всю энергию. Эти электроны не попадают на коллектор, и ток резко уменьшается.

Если энергия электронов заметно превосходит eU ₁, то такие электроны, потеряв часть своей энергии при неупругом столкновении, сохраняют достаточный избыток энергии и потому, несмотря на наличие положительно заряженной сетки, достигают коллектора, а значит, при увеличении U ток начинает возрастать. Если ускоряющий потенциал достаточно велик, так что U >> U ₁, то на оставшемся пути электрон может испытать еще одно или два (в зависимости от величины U) неупругих соударения, в результате которых атом также переходит в первое возбужденное состояние. В этом и заключается причина периодического повторения максимумов.

Величина энергии eU ₁ характеризует атомы газа, заполняющего лампу. Меньшую энергию атомы воспринять не могут, так как при такой энергии бомбардирующих их электронов удар происходит вполне упруго; энергию же eU ₁они воспринимают полностью. Но это и означает в согласии с первым постулатом Бора, что атом рассматриваемого элемента может обладать не любыми значениями энергии, а только избранными. Для сравнения на рис. 2 пунктиром изображена вольт-амперная характеристика не газонаполненной, а обычной вакуумной электронной лампы.

Для проведения опыта Франка и Герца с использованием постоянного ускоряющего напряжения необходимо применять специально изготовленные трехэлектродные лампы. Если же применять переменное ускоряющее напряжение, то можно использовать стандартные газонаполненные приборы, например, тиратроны, а вместо гальванометра применять в цепи коллектора осциллограф.

Электрическая схема используемой в данном варианте работы установки имеет вид, изображенный на рис. 3. Источником переменного напряжения, приложенного между сеткой C и катодом Kтиратрона T, служит звуковой генератор. Накал катода осуществляется от понижающего трансформатора.

Установка работает следующим образом. Переменное напряжение, приложенное между сеткой и катодом, периодически меняет энергию электронов. При этом первый полупериод лампа заперта, так как на катоде оказывается положительный потенциал. Во второй полупериод через лампу идет электронный ток. Тормозящее поле создается за счет падения напряжения на сопротивлении R (присоединенном к аноду A, являющемуся собирающим электродом) в результате прохождения через него тока.

На вертикально отклоняющие пластины осциллографа подается напряжение, снятое с сопротивления R, которое пропорционально току. На горизонтально отклоняющие пластины осциллографа подано напряжение горизонтальной развертки (рис. 4.а). При синхронности напряжения развертки и сеточного напряжения (а, следовательно, и напряжения, снимаемого с сопротивления R), на экране наблюдаются неподвижные осциллограммы, на которых отклонение электронного луча пропорционально току в лампе. Однако, отклонение луча происходит вниз, и поэтому картина, наблюдаемая на экране осциллографа (рис. 4.б) оказывается «перевернутой» по отношению к вольт-амперной характеристике, изображенной на рис. 2: минимумам этой характеристики соответствуют максимумы на экране и наоборот, максимумам - минимумы.

Картина, наблюдаемая при этом на экране осциллографа, поясняется рисунком 5. По мере повышения напряжения на сетке импульсы тока через сетку увеличиваются по амплитуде (рис. 5.а) до тех пор, пока напряжение U _С не станет равным такому U ₁, при котором начнутся неупругие столкновения электронов с атомами газа, заполняющего тиратрон (рис. 5.б). При дальнейшем увеличении U _С на осциллограмме тока появляется первый максимум (рис. 5.в), который растет по мере приближения U _Ск U ¢, то есть к напряжению, соответствующему первому минимуму вольт-амперной характеристики лампы (см. рис. 2). Если напряжение U _С продолжать увеличивать, то амплитуда импульсов тока вновь начнёт расти вплоть до напряжения U _С2 = U ₂ (рис. 5.в), при котором электроны на пути от катода к аноду станут испытывать уже не одно, а два упругих столкновения. При ещё больших значениях U _С то на экране можно наблюдать появление второго максимума осциллограммы (что соответствует второму минимуму на рис. 2).

При достижении резонансного потенциала в лампе наблюдается резонансное свечение, связанное с переходом атомов инертного газа с первого возбужденного уровня на основной. Резонансный потенциал удобно определять по разности напряжений, соответствующих появлению первого и второго максимумов. Зная резонансный потенциал, можно определить разность энергий двух стационарных состояний с n = 2 и n = 1.

Е ₂ – Е ₁ = h ν_I = e (U _С2 – U _С1) = e (U ₂ – U ₁) (8)

и излучаемую длину волны

l_I = , (9)

где е – заряд электрона, с – скорость света в вакууме. Проводя измерения, следует помнить, что амплитудное значение напряжения на сетке U _С = U _Г, где U _Г – показания вольтметра звукового генератора.

Порядок выполнения работы

1. Соберите электрическую цепь в соответствии со схемой, изображенной на рис. 4.

2. Включите трансформатор накала.

3. Включите звуковой генератор и подайте напряжение на сетку. Частота подаваемого сигнала: 200 ¸ 300 Гц.

4. Включите осциллограф в сеть и получите изображение светящейся полосы на экране.

5. Подбирая частоту развертки, усиление и фокусировку электронного луча, добейтесь неподвижного, четкого и яркого изображения на экране осциллограммы с одним минимумом (рис. 5.а – пунктирная линия, рис. 5.б – сплошная линия).

6. Плавно увеличивая ускоряющее напряжение с помощью регулятора выхода звукового генератора, получите осциллограмму с двумя минимумами (рис. 5.в). Уменьшите ускоряющий потенциал до тех пор, пока максимумы и минимумы не исчезнут. Этим заканчивается предварительная настройка схемы.

ВНИМАНИЕ: из-за конструктивных особенностей установки картина на экране осциллографа является несимметричной.

7. Установите частоту сигнала генератора равной 200 Гц и, увеличивая ускоряющее напряжение, одновременно наблюдайте за показаниями вольтметра на панели звукового генератора. Запишите показания вольтметра U = U ₁ при котором начинается спад вольт-амперной характеристики лампы (рис. 5.б – сплошная линия максимальной амплитуды), зарисуйте полученную осциллограмму.

Увеличивайте ускоряющий потенциал до тех пор, пока амплитуда осциллограммы тока через лампу на экране осциллографа вновь не достигнет максимального значения (рис. 5.в – сплошная линия), после чего запишите показания вольтметра U = U ₂ и зарисуйте полученную осциллограмму. Измерения повторите три раза, данные занесите в таблицу 2.

Таблица 2

№	U _Г1, В	U _С1, В	U _Г2, В	U _С2, В	U _С2- U _С1, В	Е ₂– Е ₁, Дж	l₁, нм	l₁_СР, нм;
200 Гц


250 Гц


300 Гц


l_СР ± Dl, нм =	Газ, заполняющий лампу:

8. Измерения, описанные в п. 7, повторите при частоте сигнала генератора, равной 250 Гц (три раза) и при частоте 300 Гц (три раза). Данные занесите в табл. 2.

9. Исходя из полученных данных, определите по формуле (8) разность значений энергии атомов инертного газа в первом возбужденном и основном стационарном состояниях.

10. Пользуясь полученными значениями Е ₂– Е ₁, вычислите длину волны излучения по формулам (8) – (9) и ее среднее значение l_СР.

11. Рассчитайте ошибку измерения длины волны по формуле:

Dl= a 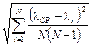, (10)

где N = 9 – число измерений; a-коэффициент Стьюдента, значения которого можно найти в таблице, имеющейся в лаборатории (таблица приведена также в методических указаниях [4]). Величину доверительной вероятности при выборе коэффициента Стьюдента по этой таблице примите равной 0,95.

12. После округления ошибки Dl и последующего округления величины l_СР (до знака, соответствующего ошибке) запишите в таблицу 2 результат измерений в виде l_СР ± Dl, нм.

11. Сверив полученный результат со значениями, приведенными в табл. 1, определите, каким газом наполнен тиратрон. Данные занесите в табл. 2.

Контрольные вопросы

1. Дайте формулировку постулатов Бора.

2. Изложите сущность опытов Франка и Герца.

3. Каким образом получают неподвижное изображение осциллограмм с максимумами на экране осциллографа?

4. Как, зная энергию перехода атома с основного уровня на возбужденный, определить частоту поглощаемого кванта?

5. Рассчитайте, исходя из теории Бора, радиусы электронных орбит водородоподобного атома.

6. Покажите, что целое число n, входящее в формулу второго постулата Бора, равно числу длин волн де Бройля, укладывающихся на длине круговой орбиты.

Список литературы

1. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Высш. шк., 2000. – С. 294.

2. Трофимова Т.И. Курс физики. – М.: Высшая школа. – 2000.

3. Селезнёв В.А., Тимофеев Ю.П. Методические указания к вводному занятию в лабораториях кафедры физики. – М.: МИИТ, 2006.

Работа 66

РЕЛЯТИВИСТКИЕ ЗАКОНЫ ДВИЖЕНИЯ МИКРОЧАСТИЦ

Цель работы. Знакомство с законами движения микрочастиц, определение их масс и времени жизни.

Приборы и принадлежности: фотографии с треками элементарных частиц, транспортир, линейка, график зависимости импульса частиц от длины свободного пробега (вывешен в лаборатории).

Введение

Классическая механика Ньютона описывает движение макроскопических тел со скоростями много меньшими, чем скорость света в вакууме. Движение тел со скоростями, близкими к этой скорости, подчиняется законам релятивистской механики, являющейся частью созданной Эйнштейном специальной теории относительности. Таким образом, для описания движения быстрых микрочастиц, в частности элементарных частиц, имеющих большую энергию, необходимо использовать релятивистскую, а не классическую механику.

Особенностью многих элементарных частиц является то, что они нестабильны и превращаются в другие, имея при этом чрезвычайное малое время жизни. Однако, основные законы сохранения (закон сохранения электрического заряда, закон сохранения импульса и закон сохранения энергии, записанный в релятивистской форме) выполняются и при взаимных превращениях частиц. Именно поэтому использование этих законов является чрезвычайно мощным средством анализа процессов, происходящих в микромире; настоящая работа является тому подтверждением.

В данной лабораторной работе изучаются частицы, называемые K-мезоном и L-гипероном, которые возникают при столкновении других частиц, p-мезонов, с ядрами некоторых атомов, а затем превращаются снова в p-мезоны и протоны. О некоторых свойствах их можно судить по фотографиям тех следов (треков), которые эти частицы оставляют в специальном приборе для регистрации микрочастиц – пузырьковой камере.

Рабочий объем пузырьковой камеры* заполнен жидкостью, находящейся в неустойчивом, перегретом состоянии. Быстро летящая частица ионизирует на своем пути молекулы жидкости, заполняющей камеру. Ионы становятся центрами интенсивного парообразования, и вдоль траектории заряженной частицы появляются пузырьки пара. Образованные этими пузырьками треки фотографируют и исследуют.

Так как, ионизируя молекулы, частица теряет свою энергию и останавливается, то по длине свободного пробега можно судить о её первоначальных энергии и импульсе. В данной лабораторной работе связь первоначального импульса 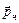частиц с длиной l свободного пробега считается известной и задаётся в виде графика, который имеется в лаборатории. Общий вид этого графика приведён на рис. 1.

Если камеру поместить в магнитное поле, то траектория заряженной частицы искривится, так как на такую частицу в магнитном поле действует сила, перпендикулярная скорости. По тому, в каком направлении искривится траектория, можно определить знак заряда частицы.

Для получения фотографий, изучаемых в настоящей работе, пузырьковая камера была облучена пучком p-мезонов (пионов). При столкновении их с ядрами вещества, заполняющего камеру, образовались К-мезоны. Они могут быть заряженными (К⁺- и К^--мезоны) или нейтральными (К⁰-мезоны). Значок справа вверху у символа частицы указывает на знак заряда или его отсутствие. По величине заряд элементарной частицы равен заряду электрона, масса К-мезонов примерно в 1000 раз больше его массы (М» 1000 m _e). Продолжительность жизни этих частиц невелика (t = 10^-¹⁰ ¸ 10^-⁸ с).

Гипероны являются более тяжелыми частицами. Изучаемый в работе L⁰-гиперон имеет массу примерно в 2200 раз большую массы электрона (М» 2200 m _e) и короткое время жизни (t = 10^-¹⁰ с).

Так как К-мезоны и L⁰-гиперон живут недолго, то на фотографиях удаётся зафиксировать следы продуктов их распада, по которым можно изучать свойства самих распавшихся частиц. На предлагаемых для изучения при выполнении лабораторной работы фотографиях можно видеть следы одного из следующих превращений:

K⁰ ® p⁺+ p^-,

L⁰ ® p + p^-,

K⁺ ® p⁺ + p⁺ + p^-.

Эти превращения схематически изображены на рис. 2.а и рис. 3.а. Протон обозначают символом p (знак заряда у протона не ставят, так как он всегда положителен); p-мезоны обозначают символами p⁺и p^-.

Как мы уже говорили, в превращениях элементарных частиц важную роль играют законы сохранения электрического заряда, импульса и энергии. Импульс распавшейся частицы в соответствии с законом сохранения импульса равен векторной сумме импульсов частиц – продуктов распада:

= .

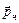Так как импульс принято обозначать той же буквой, что и протон, то в случае импульса мы будем добавлять к ней индекс «ч». В частности, выражение для импульса частицы имеющей массу m и скорость , в релятивистском случае имеет вид:

= ,

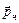где с = 3×10⁸ м/с – скорость света в вакууме.

По закону сохранения энергии полная энергия распавшейся частицы равна сумме полных энергий образовавшихся частиц: Е = .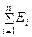

Формулу для энергии запишем в релятивистской форме:

Е = .

Основываясь на законах сохранения и измеряя длину пробега продуктов распада, можно найти некоторые характеристики распавшихся частиц.

Рассмотрим распад нейтральный частицы (К⁰, L⁰) на две заряженные. На рис. 2.а, изображающем треки частиц в пузырьковой камере, слева дан трек первичного p-мезона (первичный пучок падает слева направо). При столкновении с ядром жидкости, заполняющей пузырьковую камеру, он породил несколько частиц, разлетевшихся в разные стороны («звезда»). Среди них была и нейтральная, которая в пузырьковой камере не оставила следа. На рисунке ее траектория изображена пунктиром. Эта частица короткоживущая, она вскоре распалась на две заряженные частицы, которые оставили в камере след. По длине их пробега можно судить о первоначальных кинетической энергии частиц и импульсе. Так как пузырьковая камера находилась в магнитном поле, то треки этих частиц оказались искривленными в противоположные стороны. Обозначим импульс нейтральной частицы р _ч, импульсы продуктов ее распада р _ч1 и р _ч2, углы разлета продуктов распада j₁ и j₂ (рис. 2.б).

Пользуясь законом сохранения импульса и рис. 2.б, получаем:

р _ч1 cos j₁ + р _ч2 cos j₂ = р _ч, (1)

р _ч1 sin j₁ = р _ч2 sin j₂. (2)

В соответствии с законом сохранения энергии

= +

После сокращения на c получаем:

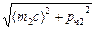= + , (3)

где M, m ₁, m ₂ – массы распавшейся частицы и продуктов распада. По известным импульсам и массам продуктов распада из этих уравнений можно вычислить массу и импульс распавшейся нейтральной частицы.

Время жизни нейтральной частицы можно определить, измеряя длину ее пролета l, т.е. расстояния, пройденного частицей от момента её образования до распада. Зная импульс распавшейся частицы р _ч, рассчитаем время ее жизни t_лаб в лабораторной системе отсчета, то есть в системе отсчёта, связанной с лабораторией. Для этого выразим t_лаб через скорость частицы u:

t_лаб = . (4)

В соответствии с теорией относительности время жизни t в системе отсчета, связанной с частицей (относительно нее частица покоится), является наименьшим и вычисляется по формуле:

t = t_лаб .

Используя формулу (4), запишем:

t = = M.

Учитывая, что для релятивистского импульса

= ,

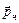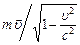в результате получаем:

t = M. (5)

По этой формуле можно вычислить время жизни частицы.

Рассмотрим далее распад заряженной частицы K ⁺ -мезона (см. рис. 3), которая превращается в три p-мезона. Как это показывают многочисленные эксперименты, при таком превращении суммарный импульс продуктов распада оказывается близким к нулю. Это значит, что K ⁺ -мезон перед распадом почти останавливается (p _ч» 0). Тогда по закону сохранения энергии

Mc ² = .

Из этого равенства, зная импульсы и массы продуктов распада, можно определить массу K ⁺ -мезона:

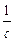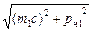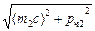M = [ + + ]. (6)

Порядок выполнения работы

Материалом для работы служат снимки, полученные в пузырьковой камере. Изображение на снимке уменьшено в два раза.

I. Изучение распада нейтральных частиц

1. На фотографиях, предложенных для обработки, отыщите двухчастичный распад нейтральной частицы.

2. Наложив на фотографию чистый лист кальки, отметьте точку рождения нейтральной частицы, точку ее распада и следы вторичных частиц.

3. Проведите линии пролета нейтральной частицы (пунктиром) и направления вылета продуктов распада. Измерьте (учитывая масштаб фотографии) длину пролета нейтральной частицы, длины пробегов продуктов распада, углы разлета частиц (см. рис. 2.а, б).

4. По графику, имеющемуся в лаборатории, определите импульс продуктов распада. Результаты занесите в табл. 1.

Таблица 1

Длина пролёта l₀, см	Природа вторичных частиц (p⁺, p^-, p)	Углы разлета продуктов распада	Длины пробега продуктов распада, см	Импульсы продуктов распада
l ₀=		j₁ = j₂ =	l ₁= l ₂=	р_ч ₁ = р_ч ₂ =

5. Вычислите по формулам (1) и (3) импульс и массу нейтральной частицы. Если пробег одной из частиц нельзя определить по фотографии (отмечено, что пробег не окончен), то для вычислений следует воспользоваться также формулой (2). Сравните массу нейтральной частицы с массой электрона. Массы протона, p-мезона и электрона даны в табл. 2, в которой для удобства расчетов приведены также значения выражения (mc)².

Таблица 2

Частицы	Масса частиц, m, кг	(mc)², кг ²× м ²× с ^-²
Протон (p) Пи-мезон (p) Электрон (е)	1,672×10^-²⁷ 2,50×10^-²⁸ 9,11 10^-³¹	2,516×10^-³⁷ 5,62×10^-³⁹ 7,47×10^-⁴⁴

6. Вычислите по формуле (5) время жизни нейтральной частицы в той системе отсчета, в которой она покоится. Результаты расчетов занесите в табл. 3.

Таблица 3

Импульс, кг×м/c	Масса частицы	Время жизни, с
кг	по отношению к массе электрона

II. Изучение распада К⁺ - мезона

1. На фотографиях отыщите распад К⁺-мезона. Перерисуйте на чистый лист кальки треки частиц.

2. Измерьте углы вылета p-мезонов по отношению к направлению импульса К⁺-мезона.

3. Измерьте пробеги p-мезонов с учетом масштаба фотографии.

4. По графику определите импульсы продуктов распада. Вычислите векторною сумму этих импульсов, найдите ее модуль и получите импульс распавшегося К⁺-мезона. Убедитесь, что он много меньше импульса каждого из p-мезонов (p _ч» 0).

5. Пользуясь формулой (6), вычислите массу К⁺-мезона. Сравните ее с массой электрона. Результаты расчётов занесите в табл. 4.

Таблица 4

Угол вылета p-мезона	Пробег p-мезона, см	Импульс p-мезона, кг×м/c	Суммарный импульс, кг×м/c	Масса К ⁺-мезона
кг	по отношению к массе электрона
j₁ = j₂ = j₃ =	l ₁ = l ₂ = l ₃ =	р _ч1 = р _ч2 = р _ч3 =	=

Контрольные вопросы

1. Объясните принцип работы пузырьковой камеры.

2. Запишите закон сохранения импульса применительно к превращению элементарных частиц. Запишите выражение для импульса частицы в релятивистской форме.

3. Запишите закон сохранения энергии при превращении элементарных частиц.

4. Как зависит время жизни частицы от ее движения?

5. Получите расчетную формулу для вычисления времени жизни покоящейся частицы.

Список литературы

12 Следующая ⇒

Воспользуйтесь поиском по сайту: