 |
Импликация и эквивалентность
|
|
|
|
Как компьютер выполняет арифметические действия над нормализованными числами?
К началу выполнения арифметического действия операнды операции помещаются в соответствующие регистры АЛУ.
Сложение и вычитание
При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков.
В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу.
В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются. В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.
Пример 1. Сложить двоичные нормализованные числа 0.10111. 2–1 и 0.11011. 210. Разность порядков слагаемых здесь равна трем, поэтому перед сложением мантисса первого числа сдвигается на три разряда вправо:
Пример 2. Выполнить вычитание двоичных нормализованных чисел 0.10101. 210 и 0.11101. 21. Разность порядков уменьшаемого и вычитаемого здесь равна единице, поэтому перед вычитанием мантисса второго числа сдвигается на один разряд вправо:
Результат получился не нормализованным, поэтому его мантисса сдвигается влево на два разряда с соответствующим уменьшением порядка на две единицы: 0.1101. 20.
Умножение
При умножении двух нормализованных чисел их порядки складываются, а мантиссы перемножаются.
Пример 3. Выполнить умножение двоичных нормализованных чисел:
|
|
|
(0.11101. 2101). (0.1001. 211) = (0.11101. 0.1001). 2(101+11) = 0.100000101. 21000.
Деление
При делении двух нормализованных чисел из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя. Затем в случае необходимости полученный результат нормализуется.
Пример 4. Выполнить деление двоичных нормализованных чисел:
0.1111. 2100: 0.101. 211 = (0.1111: 0.101). 2(100–11) = 1.1. 21 = 0.11. 210.
Использование представления чисел с плавающей точкой существенно усложняет схему арифметико-логического устройства.
61. ЛОГИКА - это наука о законах и формах мышления, направленная на познание объективного мира. Слово логика обозначает совокупность правил, которым подчиняется процесс мышления или обозначает науку о правилах рассуждения и тех формах, в которых оно осуществляется.
Объектом логики как науки выступает абстрактное мышление. Логика изучает абстрактное мышление как средство познания объективного мира, исследует формы и законы, в которых происходит отражение мира в процессе мышления. Основными формами абстрактного мышления являются:
ПОНЯТИЯ,
СУЖДЕНИЯ,
УМОЗАКЛЮЧЕНИЯ.
ПОНЯТИЕ — форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов: портфель трапеция ураганный ветер, например, "дерево", "самолет") или группой слов, т.е. словосочетаниями, например, "студент гуманитарного института", "создатель художественных картин", "река Дон", "космический корабль" и др.
СУЖДЕНИЕ — мысль, в которой что-либо утверждается или отрицается о предметах. Суждения являются повествовательными предложениями, истинными или ложными. Они могут быть простыми и сложными: Весна наступила, и грачи прилетели. Пример сложного суждения: "Наступила осень, и лебеди улетают". Оно состоит из двух простых суждений.
УМОЗАКЛЮЧЕНИЕ — прием мышления, посредством которого из исходного знания получается новое знание; из одного или нескольких истинных суждений, называемых посылками, мы по определенным правилам вывода получаем заключение. Есть несколько видов умозаключений. Все металлы — простые вещества. Литий — металл. Литий — простое вещество.
|
|
|
Все металлы - вещества. Железо – металл. Железо - вещество
Чтобы достичь истины при помощи умозаключений, надо соблюдать законы логики.
ФОРМАЛЬНАЯ ЛОГИКА — наука о законах и формах правильного мышления.
МАТЕМАТИЧЕСКАЯ ЛОГИКА изучает логические связи и отношения, лежащие в основе дедуктивного (логического) вывода. (В книгах какого писателя хорошо рассказано о дедуктивном методе?)
Формальная логика связана с анализом наших обычных содержательных умозаключений, выражаемых разговорным языком. Математическая логика изучает только умозаключения со строго определенными объектами и суждениями, для которых можно однозначно решить, истинны они или ложны.
Основа работы логической схемы и устройств П.К- логика. В логике суждения- высказывание- повествовательное предложение- истинное или ложное.
2+8<5
5*5=25
2*2=5
Квадрат есть параллелограмм
Параллелограмм есть квадрат. -простые.
Сложные (с использованием связок и, или и частицы не.)
В М. Л. не рассматривается конкретное содержание высказывания, важно только истинно оно или ложно, поэтому высказывание можно представить некоторой ~ величиной, значение которой может быть 0 или 1
0- ложно, 1- истинно.
Для простоты записи высказывание обозначается латинскими буквами. У кошки 4 ноги А=1.
Москва расположена на 2 холмах В=0
Устройство П.К, выполняющее действие над двоичными числами, можно рассмотреть как некоторый функциональный преобразователь, причем входные числа это значения входных логических переменных, а выходное число значение логической функции, которое получено в результате выполнения определенных операций. Таким образом этот преобразователь реализует некоторую логическую функцию.
Значения логических функций при разных сочетаниях значений входных переменных (наборах входных ~) - обычно задаются специальной таблицей - таблицей истинности.
Количество наборов входных ~ (Q) определяется выражением: (Q)=2n – где n количество входных ~. таблица истинности может иметь вид
|
|
|
X Y Z F (x, y, z)
0 0 0 1
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 0
В алгебре высказываний любую логическую функцию можно выразить через основные логические операции, записать ее в виде логического выражения и упростить ее, применяя законы логики и свойства логических операций. По формуле логической функции легко рассчитать ее таблицу истинности. Необходимо только учитывать порядок выполнения логических операций (приоритет) и скобки. Операции в логическом выражении выполняются слева направо с учетом скобок.
Приоритет логических операций:
· ИНВЕРСИЯ,
· КОНЪЮНКЦИЯ,
ДИЗЪЮНКЦИЯ КОНЪЮНКЦИЯ
Конъюнкция: соответствует союзу: «и», обозначается знаком^, обозначает логическое умножение.
Конъюнкция двух логических ~ истинна тогда и только тогда, когда оба высказываний истинны. Можно обобщить для любого количества переменных А^В^С = 1 если А=1, В=1, С=1.
| А | В | А^B |
ДИЗЪЮНКЦИЯ
Логическая операция соответствует союзу ИЛИ, обозначается знаком v, иначе называется ЛОГИЧЕСКОЕ СЛОЖЕНИЕ.
Дизъюнкция двух логических переменных ложна тогда и галька тогда, когда оба высказывавия ложны.
Это определение можно обобщить для любого количества логических переменных, объединенных дизъюнкцией.
A v В v С = 0, только если А = О, В = О, С - 0.
| А | В | А v B |
ИНВЕРСИЯ
Логическая операция соответствует частице не, обозначается или ¯ и является логическим отрицанием.
Инверсия логической переменной истинна, если переменная ложна и наоборот: инверсия ложна, если переменная истинна.
А А
1 0
0 1
высказывания у которых таблицы истинности совпадают называются равносильными.
ИМПЛИКАЦИЯ и ЭКВИВАЛЕНТНОСТЬ
Импликация «если А, то В», обозначается А → В
А В А → В
0 0 1
0 1 1
1 0 0
1 1 1
Эквивалентность «А тогда В и только тогда», обозначается А ~ В
А В А~ В
0 0 1
0 1 0
1 0 0
1 1 1
При вычислении значения логического выражения (формулы) логические операции вычисляются в определенном порядке, согласно их приоритету:
|
|
|
1. инверсия,
2. конъюнкция,
3. дизъюнкция,
4. импликация и эквивалентность.
Операции одного приоритета выполняются слева направо. Для изменения порядка действий используются скобки.
Например: дана формула 
Порядок вычисления:
- инверсия
- конъюнкция
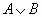- дизъюнкция
- импликация
- эквивалентность
Функции И, ИЛИ, НЕ
Функции И (AND), ИЛИ (OR), НЕ (NOT) - позволяют создавать сложные логические выражения. Эти функции работают в сочетании с простыми операторами сравнения. Функции И и ИЛИ могут иметь до 30 логических аргументов и имеют синтаксис:
=И(логическое_значение1;логическое_значение2...)
=ИЛИ(логическое_значение1;логическое_значение2...)
Функция НЕ имеет только один аргумент и следующий синтаксис:
=НЕ(логическое_значение)
Аргументы функций И, ИЛИ, НЕ могут быть логическими выражениями, массивами или ссылками на ячейки, содержащие логические значения.
пример. Пусть Excel возвращает текст "Прошел", если ученик имеет средний балл более 4 (ячейка А2), и пропуск занятий меньше 3 (ячейка А3). Формула примет вид: =ЕСЛИ(И(А2>4;А3<3);"Прошел";"Не прошел")
Не смотря на то, что функция ИЛИ имеет те же аргументы, что и И, результаты получаются совершенно различными. Так, если в предыдущей формуле заменить функцию И на ИЛИ, то ученик будет проходить, если выполняется хотя бы одно из условий (средний балл более 4 или пропуски занятий менее 3). Таким образом, функция ИЛИ возвращает логическое значение ИСТИНА, если хотя бы одно из логических выражений истинно, а функция И возвращает логическое значение ИСТИНА, только если все логические выражения истинны.
Функция НЕ меняет значение своего аргумента на противоположное логическое значение и обычно используется в сочетании с другими функциями. Эта функция возвращает логическое значение ИСТИНА, если аргумент имеет значение ЛОЖЬ, и логическое значение ЛОЖЬ, если аргумент имеет значение ИСТИНА.
|
|
|
