 |
Методические указания и примеры решения
|
|
|
|
Указания к решению задач 5.3.13 и 5.3.14
В задаче 5.3.13 при увеличении емкости на 10% «новая» wРН уменьшится
и частота внешнего воздействия w0 уже не будет равна резонансной частоте.
В общем случае для вычисления обобщенной расстройки лучше использовать точное выражение
.
В частных случаях, в области частот, близким к резонансным (в задаче 5.3.14 w= 1,005 wР, т.е. D w=w - wР= 0,005 wР), можно пользоваться приближенной формулой для x
.
Соотношение между UС и UСР зависит от x и определяется выражением (5.3). Обобщенная расстройка определяет все фазовые сдвиги в контуре: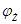 
, 
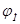и 
. Зная, что 
= arсtgx, определите 
, 
, на основании закона Ома в комплексной форме.
Указания к решению задачи 5.3.18
Индикатор резонанса не реагирует на изменения тока меньше, чем 1%, что на нормированной резонансной кривой (рисунок 5.3) соответствует уровню 0,99.
 |
Рисунок 5.3 - Нормированная резонансная кривая
Этому уровню соответствует ±xВ или частоты f1 и f2 . Искомая относительная погрешность 
, где D f=f2-fР=fР-f1, определяется зоной нечувствительности индикатора при изменении частоты относительно резонансной в любую сторону и не зависит от абсолютного значения fР.
Указания к решению задач 5.3.19-5.3.21, 5.3.23 и 5.3.24 и пример решения
В задачах, когда на контур действуют одновременно э.д.с. сигнала и э.д.с. помехи (см. рисунок 5.2), следует полагать, что контур настроен на частоту сигнала, т.е. wР=wС. В таких задачах обязательно следует представить себе “расположение” wС и wП относительно резонансной кривой (см. рисунок 5.3) и исходить из того, что на частотах wС и wП в соответствии с законом Ома величина тока в контуре определяется
, 
, (5.4)
|
|
|
а величина напряжения на емкости на основе Uc = I× | 
С | определяется как
, 
,
тогда
, (5.5)
где
x = Q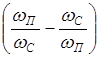 
.
Типовая задача.
На последовательный колебательный контур действуют одновременно сигнал еc(t)=1COS 16t мВ и помеха еn(t) =10 COS 5·15t мВ (рисунок 5.2). Рассчитать параметры контура, если известно, что составляющая напряжения на емкости, созданная сигналом, превышает составляющую, созданную помехой в 10 раз, а составляющая тока с частотой сигнала имеет амплитуду 0,1 мА. Определить также амплитуды обеих составляющих напряжения на емкости.
Представим резонансную кривую последовательного контура и осмыслим условие задачи с помощью рисунка 5.4.
Рисунок 5.4
Из рисунка ясно, что x П< 0 и | xП |>>1, т.к. wП = 0,5 wР ..
Если ЕС=ЕП, то в соответствии с (5.3)
и значения UCC и UCП соответствуют рисунку 5.4.
Однако, в нашем случае ЕП = 10 ЕС, тогда в силу линейности цепи
.
В общем случае, если ЕП = n × ЕС, то
.
Решение.
1) в соответствии с вышесказанным и выражением (5.5)
,
, откуда xП = -200;
2) т.к. | xП | >> 1, нельзя пользоваться приближенным выражением xП .:
или 
,
откуда 
;
3) сопротивление потерь контура 
Ом;
4) 
= 
тогда 
мГн;
5) 
тогда 
пФ;
6) UСС = ЕС ×Q = 1·133,3=133,3 мВ;
7) UСП = 
мВ.
Пример решения задачи определения эффекта шунтирования
Последовательный контур настроен в резонанс, его добротность Q = 200, | XСР | =100 Ом, EВХ =1,2 В.
Определить величину напряжения на емкости. Какое напряжение показал бы вольтметр с чисто активным входным сопротивлением RВХ = 20 кОм, если бы его подключить параллельно емкости?
 |
Решение. Представим схему последовательного контура (рисунок 5.5) с подключенным вольтметром, входное сопротивление которого 20 кОм.
Рисунок 5.5
Напряжение на емкости обозначим Uаб. Входное сопротивление вольтметра выступает как шунтирующее сопротивление. Это приводит к снижению добротности и, в конечном итоге, к уменьшению напряжения на емкости.
|
|
|
 |
Шунтирующее сопротивление RВХ необходимо пересчитать в дополнителное сопротивление потерь RДОБ, (рисунок 5.6)
Рисунок 5.6
Если RВХ»| ХС |, то СЭ ≈ С, 
;
для 
,
где r - характеристическое сопротивление (по определению - это сопротивление индуктивности или емкости на резонансной частоте).
RДОБ = 
Ом.
До включения вольтметра сопротивление потерь было
R = 
Ом.
Общее сопротивление потерь RΣ = R + RДОБ . или RΣ = 0,5 + 0,5 = 1 Ом.
Эквивалентная добротность контура с учетом RДОБ может быть рассчитана по формуле:
.
С учетом этого, напряжение на емкости UСР окажется равным:
UСР=QЭ·Е= 100·1,2=120 В.
Так как в схеме резонанс и 
, то
В,
Uаб = 
В.
Расчетное значение 
при отключенном вольтметре
В.
Вывод: на результаты измерений оказывает большое влияние входное сопротивление измерительного прибора.
Знания и умения
В результате работы над темой студент должен знать основы теории и уметь решать задачи. Конкретно следующее.
Знать:
1) понятие резонанса и условия его возникновения;
2) методику определения резонансных частот и методику определения резонансных сопротивлений для любой линейной электрической цепи, содержащей L,C,R;
3) физический смысл и выражения для wр, r, Q, Rр;
4) смысл и выражения для абсолютной, относительной и обобщенной расстроек;
5) понятие полосы пропускания и методику ее определения (расчета);
6) основные соотношения между током и напряжениями в последовательном колебательном контуре на резонансной частоте;
7) почему резонанс в последовательном колебательном контуре называется резонансом напряжений;
8) выражения и графики АЧХ или резонансных кривых для тока, напряжения на любом из элементов контура и входного сопротивления последовательного колебательного контура;
9) выражение и график ФЧХ для ZВХ;
10) влияние шунтирующего сопротивления на основные характеристики колебательного контура: добротность, полосу пропускания, входное сопротивление; методику пересчета шунтирующего сопротивления в дополнительное сопротивление потерь и выражение для RДОБ, если RШ » r;
|
|
|
11) при каких условиях последовательный контур, состоящий из L,C,R, можно назвать колебательным.
Уметь:
1) рассчитывать различными вариантами добротность контура;
2) рассчитывать фазовый сдвиг между любыми двумя электрическими величинами (
и 
, и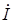 
и др.) на заданной частоте, а также ФЧХ контура;
3) рассчитывать частоты, а также все виды расстроек, соответствующие заданному значению АЧХ и ФЧХ контура;
4) решать задачу анализа прохождения двухчастотного сигнала через колебательный контур, а также решать обратную задачу (синтеза), т.е. определять требуемые параметры контура, которые обеспечат заданное ослабление помехи по сравнению с сигналом;
5) рассчитывать мощности, выделяемые в контуре на резонансной частоте и при расстройке.
Формы контроля
Тестовый опрос с целью выяснения степени подготовки по теоретическому материалу и самостоятельная работа с целью выяснения приобретенных навыков в решении задач по данной теме. Для самостоятельной работы используются задачи п. 5.3.
|
|
|
