 |
Интегрирование дифференциального бинома. Теорема Чебышева.
|
|
|
|
Первообразная. Неопределенный интеграл; его основные свойства.
· Первообразная
Первообразной функции f на промежутке I называется функция F,
такая, что 
· Неопределенный интеграл
где F - первообразная функции f (на промежутке); C - произвольная постоянная.
Основные свойства
1. ∫(f(x)d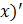 
=f(x), d∫f(x)dx=f(x)dx
2. ∫F′(x)dx=F(x)+C, ∫dF(x)=F(x)+C
3. Если ∫f(x)dx=F(x)+C, то ∫f(ax+b)dx= 
F(ax+b)+C, a≠0
4. ∫(af(x)+ßg(x))dx=a∫f(x)dx+ß∫g(x)dx, 
≠0
Таблица интегралов. Простейшие приемы интегрирования (подведение под знак дифференциала)
Метод подведения под знак дифференциала основан на равенстве 
То есть, главной задачей является приведение подынтегральную функцию к виду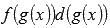 
‼таблица интегралов
‼Простейшие приемы интегрирования
Интегрирование по частям.
Пусть u (x) и v (x) являются дифференцируемыми функциями. Дифференциал произведения функций u и v определяется формулой
Проинтегрировав обе части этого выражения, получим
или, переставляя члены,
Эта формула применяется в случае, когда подынтегральная функция представляет произведение алгебраической и трансцендентной функции.
В качестве u обычно выбирается функция, которая упрощается дифференцированием, в качестве dv - оставшаяся часть подынтегрального выражения, содержащая dx, из которой можно определить v путем интегрирования.
Примеры:
Замена переменной в неопределенном интеграле.
Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:
а) 
, где 
– монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае: 
;
б) 
, где U – новая переменная. Формула замены переменной при такой подстановке: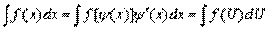 
.
|
|
|
Интегрирование рациональных дробей.
Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;
-Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;
-Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;
-Вычислить интегралы от простейших дробей.
Интегрирование функций, содержащих дробные иррациональности
Для интегрирования иррациональной функции, содержащей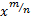 
используется подстановка u= 
.
Чтобы проинтегрировать иррациональную функцию, содержащую несколько рациональных степеней x, применяется подстановка в форме u= , где n полагается равным наименьшему общему кратному знаменателей всех дробных степеней, входящих в данную функцию.
Рациональная функция x под знаком корня n-ой степени, т.е. выражение вида 
, интегрируется с помощью подстановки u=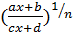 
Интегрирование выражений, содержащих тригонометрические функции (универсальная тригонометрическая подстановка).
При интегрировании выражений вида ∫R(cos x;sin x) dx обычно используют следующие подстановки:
а) если R(- cos x;sin x) = -R(cos x;sin x), то t = sin x;
б) если R(cos x; - sin x) = -R(cos x;sin x), то t = cos x;
в) если R(- cos x; - sin x) = R(cos x;sin x), то t = tg x
Подстановки Эйлера. (Интегрирование рационального выражения от корня из квадратного трехчлена.)
Подстановки Эйлера — приводящие интегралы вида 
, где 
— иррациональная функция, к интегралам от рациональных функций.
Первая подстановка
Используется тогда, когда a>0. Производится замена:
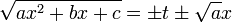
Вторая подстановка
Используется тогда, когда с>0. Производится замена:
Третья подстановка
Используется тогда, когда подкоренное выражение имеет два действительных корня. Производится замена:
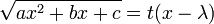, где 
— один из корней.
|
|
|
Интегрирование дифференциального бинома. Теорема Чебышева.
Интегрирование диф. бинома (теорема Чебышёва)
Интеграл ∫ 
dx, где m, n, p є Q, можно привести к интегрированию рациональных функций в следующих случаях:
1) p є Z: замена x = 
, где N — общий знаменатель m и n;
2) 
є Z: замена a + b 
, где N — знаменатель p;
3) 
є Z: замена a 
+b= , где N — знаменатель p
|
|
|
