Методики выполнения измерений

Измерения при проведении испытаний

 

1.1 Эталоны и стандартные образцы

 

Эталон — это высокоточная мера, предназначенная для воспро­изведения и хранения единицы физической величины для передачи ее размера другим средствам измерения. От эталона единица физической величины передается разрядным эталонам, а от них к рабочим средствам измерения.

Государственный (национальный) эталон единицы величины — эталон единицы величины, признанный решением уполномоченного на то федерального органа в качестве исходного на тер­ритории своего государства.

Эталоны классифицируют на первичные, вторичные и рабочие.

Первичный эталон — это эталон, воспроизводящий единицу физической величины с наивысшей точностью.

Первичному эталону соподчинены вторичные и рабочие (разрядные) эталоны. Вторичные эталоны иногда называют «эталоны — копии».

Рабочие эталоны воспринимают размер единицы от вторичных эталонов и служат для передачи размера менее точному рабочему эталону (если существует эталон более низкого разряда) или рабочим средствам измерений, инструменту.

 

Стандартные образцы состава, свойств веществ и материалов внесены в российский государственный Реестр средств измерений, который содержит около 10 тыс. типов стандартных образцов (СО), используемых для метрологического обеспечения контроля — градуировки средств измерений.

Стандартные справочные данные внесены в банк данных о свойствах материалов и веществ, ведение которого поручено Государственной службе стандартных справочных данных (ГСССД) о физических константах и свойствах материалов и веществ. Для норм и правил, обеспечивающих применение этих данных, установлены следующие категории справочных данных:

· ССД — числовые значения физических констант или свойств материалов и веществ, полученные на основе анализа всей известной совокупности результатов измерений (испытаний, расчетов), аттестованные и утвержденные Госстандартом РФ. Официальным изданием ССД являются «Таблицы стандартных справочных данных»;

· РСД — числовые значения физических констант или свойств материалов и веществ, полученные на основе оценки погрешности результатов их определения (измерений, испытаний, расчетов), аттестованные и утвержденные Научно-исследовательским центром по материалам и веществам (ВНИЦ MB) Госстандарта России.

Информационные данные — это фактографические сведения о материалах и веществах, не прошедших или не подлежащих аттестации в ГСССД, к ним относятся:

· числовые значения физических констант или свойств, до­стоверность (погрешность) которых не установлена;

· данные о номенклатуре и технико-экономических показателях материалов и веществ, содержащихся в информаци­онных, регистрационных и нормативно-технических документах, в том числе числовые данные о свойствах веществ, если не указана их категория;

· сведения библиографического и адресно-тематического характера, полученные на основе оценки погрешности результатов их определения (измерений, испытаний, расчетов).

Шкалы измерений

Шкала средства измерений — это упорядоченная совокупность отметок и цифр, соответствующая ряду последовательных значений измеряемой величины.

В шкале Цельсия за начало отсчета принята температура таяния льда, а в качестве основного интервала (опорной точки) температура кипения воды. Одна сотая часть этого интервала — градус Цельсия (°С), является единицей температуры.

В метрологической практике известны несколько разновидностей шкал: шкала наименований, шкала порядка, шкала интервалов, шкала отношений, абсолютные шкалы, условные шкалы.

Шкалы наименований — это качественные шкалы, которые не содержат нуля и единиц измерений, здесь отсутствуют отноше­ния типа «больше — меньше». Примером может служить шкала цветов (атлас цветов). Измерение заключается в визуальном сравнении окрашенного предмета с образцами цветов (эталонными образцами атласа цветов). Так как каждый цвет имеет множество оттенков, такое сравнение под силу эксперту, который имеет не только опыт, но и обладает соответствующими особыми характеристиками возможностей визуального наблюдения.

Шкалы порядка. Свойства величин описывают как отношением эквивалентности, так и отношением порядка по возрастанию или убыванию количественного проявления свойства. В этих шкалах может иметься нулевая отметка, но отсутствуют единицы измерения, поскольку невозможно установить, в какое число раз больше или меньше проявляется свойство величины. Обычно шкалы порядка характеризуют значение измеряемой величины (сила землетрясения, сила ветра и т.п.) в баллах.

Шкала интервалов (разностей). Описывать свойства величин можно не только с помощью отношений эквивалентности и порядка, но и с применением суммирования и пропорциональности интервалов (разностей) между количественными проявлениями данного свойства. Шкалы интервалов имеют условные нулевые значения, а интервалы устанавливаются по согласованию. Такими шкалами являются шкалы времени и длины.

Шкала отношений имеет естественное нулевое значение, а единица измерений устанавливается по согласованию. Например, шкала весов, начинаясь с нулевой отметки, может быть градуирована по-разному в зависимости от требуемой точности взвешивания.

Абсолютные шкалы всегда имеют определение единицы измерения физической величины.

Условные шкалы — это шкалы физических величин, исходные значения которых выражены в условных единицах, иногда их называют неметрическими. К ним относятся шкалы твердости минералов и металлов.

 

1.3 Точность измерения

 

Точность измерения — это степень приближения результатов измерения к некоторому действительному значению физической величины. Чем меньше точность, тем больше погрешность измерения и, соответственно, чем меньше погрешность, тем выше точность.

Даже самые точные приборы не могут показать действительного значения измеряемой величины. Обязательно существует погрешность измерения, причинами которой могут быть различные факторы.

 

Погрешности могут быть:

· систематические, например, если тензосопротивление плохо наклеено на упругий элемент, то деформация его решетки не будет соответствовать. деформации упругого элемента и датчик будет постоянно неправильно реагировать;

· случайные, вызванные, например, неправильным функцио­нированием механических или электрических элементов измерительного устройства;

· грубые, как правило, допускаются самим исполнителем, который из-за неопытности или усталости неправильно считывает показания прибора или ошибается при обработке информации. Их причиной могут стать и неисправность средств измерений, и резкое изменение условий измерения.

Полностью исключить погрешности практически невозможно, а вот установить пределы возможных погрешностей измерения и, следовательно, точность их выполнения необходимо.

Погрешностью измерения ∆(Х_ИЗМ) называют отклонение результата измерения (X) от истинного или действительного значе­ния (Х_И или Х_Д) измеряемой величины:

Погрешность может быть абсолютной, относительной и при­веденной.

Абсолютная погрешность измерения (∆) представляет собой разность между измеренной величиной и истинным или действительным значением этой величины, т. е. ∆=Х- или .

Относительная погрешность измерения (δ) представляет собой отношение абсолютной погрешности измерения к действительному значению измеряемой величины. Относительная погрешность может выражаться в долях, тогда 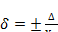, или в процентах, тогда .

Приведенная погрешность измерения (γ) представляет собой отношение абсолютной погрешности к нормированному значению величины, например, ее максимальному значению, т. е. , где X_N — нормированное значение величины,

X_N=Х_max (Х_max — максимальное значение измеряемой величины).

При многократных измерениях в качестве истинного значения, как правило, используют среднее арифметическое значение:

 

(1.1)

 

В отличие от относительной и приведенной абсолютная погрешность всегда имеет ту же размерность, что и измеряемая величина.

Величина X, полученная в одной серии измерений, является случайным приближением к . Для оценки ее возможных отклонений от определяют среднее квадратическое отклонение:

(1.2)

Для оценки рассеяния отдельных результатов измерения () относительно среднего арифметического значения Х_ср определяют среднеквадратическое отклонение:

при n ≥ 20

или (1.3)

при n < 20

 

Применение формул (1.3) правомерно при условии постоянства измеряемой величины в процессе измерения. Если при измерении величина изменяется, как, например, при измерении потенциала проводника через равные отрезки длины, то в формулах (1.3) в качестве Х_ср следует брать какую-то постоянную величину, например, начало отсчета.

Формулы (1.2) и (1,3) соответствуют центральной предельной теореме теории вероятностей, согласно которой

(1.4)

Среднее арифметическое значение из ряда измерений всегда имеет меньшую погрешность, чем погрешность каждого определенного измерения. Это и отражает формула (1.4), определяющая фундаментальный закон теории погрешностей, из которого следует, что если необходимо повысить точность результата (при исключенной систематической погрешности) в 2 раза, то число измерений нужно увеличить в 4 раза; если требуется точность в 3 раза, то число измерений увеличивается в 9 раз и т. д.

Нужно четко разграничивать применение : величина используется при оценке погрешностей окончательного результата, а — при оценке погрешности метода измерения.

Случайная (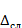) и систематическая () составляющие погрешности измерения проявляются, как правило, одновременно. Общая погрешность при их независимости определяется их суммой или через среднеквадратическое отклонение

.

Значение случайной погрешности заранее неизвестно, оно возникает из-за множества неуточненных факторов.

Для уменьшения случайной погрешности есть два пути: или повышать точность измерений (уменьшение ), или увеличивать числа измерений (n).

Если считать, что все возможности совершенствования техники измерений использованы, то остается только второй путь. При этом отметим, что уменьшать случайную составляющую погрешности целесообразно лишь до тех пор, пока общая погрешность измерений не будет полностью определяться систематической составляющей ∆c

Если систематическая погрешность определяется классом точности средств измерения (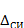), то необходимо, чтобы доверительный интервал где — коэффициент Стьюдента, был существенно меньше .

Обычно принимают при доверительной вероятности Р =0,95.

В случае невозможности выполнения этого условия необходимо коренным образом изменить методику измерения.

При сравнении случайных погрешностей с различными законами распределения использование показателей, которые сводят плотность распределения к одному или нескольким числам, обязательно. Такими числами могут быть среднеквадратическое отклонение, доверительный интервал (от ) и доверительная вероятность. Надежность самого среднеквадратического отклонения(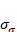) определяется по формуле .

Принято считать, что если , то оценка точности надежна. Это условие выполняется уже при n = 8.

На практике важно уметь правильно сформулировать требования к точности измерений. Например, если за допустимую погрешность измерения принять то, повышая требования к контролю (например, до 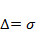), при сохранении технологии из­готовления изделий увеличивается вероятность брака.

Наиболее вероятная погрешность () отдельного измерения определяется по формуле

Таким образом, с увеличением n значение вероятной погрешности быстро уменьшается, но лишь до n ≈ 5. Следовательно, увеличение числа измерений на одном режиме больше 5 нецелесообразно, что соответствует условию получения надежных значений .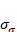

Число измерений определяют, используя одно из выражений:

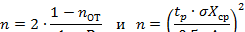
где — число отбрасываемых экспериментальных результатов.

С учетом коэффициентов Стьюдента можно оценить относительную погрешность отдельного измерения:

и его среднего значения:

Считается, что систематические погрешности могут быть об­наружены и исключены. Однако в реальных условиях полностью исключить систематическую составляющую погрешности невозможно. Всегда остаются какие-то неисключенные факторы, которые нужно учитывать, и которые будут систематической погрешностью измерения. То есть, систематическая погрешность тоже случайна, и ее определение обусловлено лишь установившимися традициями обработки и представления результатов измерения.

Необнаруженная систематическая составляющая погрешности опаснее случайной: если случайная составляющая вызывает вариацию (разброс) результатов, то систематическая - устойчиво их искажает (смещает). В любом случае отсутствие или незначительность (пренебрежение) систематической погрешности надо доказать.

Действительно, если взять два ряда измерений одной и той же величины, то средние результаты этих рядов, как правило, будут различны. Это расхождение может быть определено случайной или систематической составляющей.

Последовательность выявления характера погрешности следующая.

1 Из двух рядов 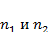независимых измерений находят средние арифметические значения Х_ср1 и Х_ср2.

2 Определяют значение

3 Вычисляют

4 Является или нет разность случайной величиной устанавливают из выражения ,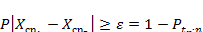

где 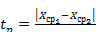; Здесь Р- доверительная вероятность того, что результат измерения отличается от истин­ного на величину не более чем

Величина Р определяется по таблице Стъюдента.

Если Р > 0,95, то разность носит систематический характер.

Таким образом, для характеристики случайной погрешности надо обязательно задать два числа: величину самой погрешности (или доверительный интервал от и доверительную вероятность.

 

 

В отличие от случайной погрешности, выявленной в целом вне зависимости от ее источников, систематическая погрешность рассматривается по составляющим в зависимости от источников ее возникновения, причем различают методическую, инструментальную и субъективную составляющие погрешности.

P	n
0,01	1,73	2,16	2,43	2,62	2,75	2,90	3,08
0,02	1,72	2,13	2,37	2,54	2,66	2,80	2,96
0,05	1,71	2,1	2,1	2,41	2,52	2,64	2,78
0,1	1,69			2,29	2,39	2,49	2,62

Субъективная составляющая погрешности связана с индивидуальными особенностями оператора. Как правило, она возникает из-за ошибок в отсчете показаний (примерно 0,1 деления шкалы) и неопытности оператора.

В основном же систематические погрешности возникают из-за методической и инструментальной составляющих.

Методическая составляющая погрешности обусловлена несо­вершенством метода измерения, приемами использования средств измерения, некорректностью расчетных формул и округления результатов.

Инструментальная составляющая погрешности возникает из-за собственной погрешности средств измерения, определяемой классом точности, влиянием средств измерения на результат и ограниченной разрешающей способности средств измерения.

Целесообразность разделения систематической погрешности на методическую и инструментальную составляющие определяется следующим:

· для повышения точности измерений можно выделить лимитирующие факторы и принять решение об усовершенствовании методики или выборе более точных СИ;

· появляется возможность определить составляющую общей погрешности, увеличивающейся со временем или под влиянием внешних факторов, pi целенаправленно осуществ­лять периодические поверки и аттестации;

· инструментальная составляющая может быть оценена до разработки методики, а потенциальные возможности точности определит только методическая составляющая.

Таким образом все виды составляющих погрешности нужно анализировать и выявлять в отдельности, а затем суммировать их в зависимости от характера, что является основной задачей при разработке и аттестации методик выполнения измерений.

В ряде случаев систематическая погрешность может быть исключена путем устранения источников погрешности до начала измерений (профилактика погрешности), а в процессе измерений — путем внесения известных поправок в результаты измерений.

Профилактика — наиболее рациональный способ снижения погрешности и заключается в устранении влияния, например, температуры (термостатированием и термоизоляцией), магнитных полей (магнитными экранами), вибраций и т. п. Сюда же относятся регулировка, ремонт и поверка средств измерений.

Исключение постоянных систематических погрешностей в процессе измерений осуществляют методом сравнения (замещения, противопоставления), компенсации по знаку (предусматривают два наблюдения, чтобы в результат каждого измерения систематическая погрешность входила с разным знаком), а исключение переменных и прогрессирующих — способами симметричных наблюдений или наблюдением четное число раз через полупериоды.

Грубые погрешности измерений могут сильно исказить Х_ср, σ и доверительный интервал, поэтому их исключение обязательно. Обычно они сразу видны в ряду полученных результатов, но в каждом конкретном случае это необходимо доказать. Существует Рид критериев для оценки промахов.

Критерий Зσ. В этом случае считается, что результат, возникающий с вероятностью Р ≤ 0,003, малореален и его можно квалифицировать промахом, т. е. сомнительный результат отбрасывается, если .

Величины Х_ср и σ вычисляют без учета Данный критерий надежен при n ≥ 20.

При п < 20, как правило, применяют критерий Романовского. В этом случае используют уровень значимости β, который определяется равенством . Полученное значение сравнивают со значением, полученным теоретически (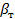) в зависимости от числа измерений (n) и выбираемой вероятности (P) (см. табл. 1.1).

Обычно Р находится в пределах 0,01—0,05, и если β≥ , то результат отбрасывают.

Если число измерений невелико (до 10), то используют критерий Шовине. В этом случае промахом считается результат X_i, при котором разность в зависимости от числа измерений (n) превышает значения :

1.6 при n = 3;

1.7 при п = 6;

1,9 при п = 8;

2 при п = 10.

Погрешность измерений как характеристику точности измерений нормируют в виде предела 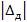допускаемых значений погрешности средств измерений данного типа.

Основные задачи нормирования погрешностей заключаются в выборе показателей, характеризующих погрешность, и установлении допускаемых значений этих показателей. Решение данных задач определяется целью измерений и использованием результатов. Например, если результат измерения используется наряду с другими при расчете какой-то экспериментальной характеристики, то необходимо учитывать погрешности отдельных составляющих путем суммирования их среднеквадратических отклонений.

Если речь идет о контроле в пределах допуска и нет информации о законах распределения параметра и погрешности, то достаточно ограничиться доверительным интервалом с доверительной вероятностью. Эти показатели должны сопровождать результаты измерений тогда, когда дальнейшая обработка результатов не предусмотрена.

Поэтому для оценки погрешностей измерений необходимо установить вид модели погрешности с ее характерными свойствами, определить характеристики этой модели и оценить показатели точности измерений по характеристикам модели.

При установлении модели погрешности возникают типовые статистические задачи: оценка параметров закона распределения, проверка гипотез, планирование эксперимента и др.

Точность измерения может выражаться следующим:

· интервалом, в котором с установленной вероятностью находится суммарная погрешность измерения;

· интервалом, в котором с установленной вероятностью на­ходится систематическая составляющая погрешности измерений;

· стандартной аппроксимацией функции распределения случайной составляющей погрешности измерения и среднеквадратическим отклонением случайной составляющей погрешности измерения;

· стандартными аппроксимациями функций распределения систематической и случайной составляющих погрешности измерения и их средними квадратическими отклонениями и функциями распределения систематической и случайной составляющих погрешности измерения.

На практике применяется, как правило, первый способ при Р = 0,9). Например, система допусков построена на понятии предельной погрешности при Р = 0,95, т. е. максимальной погрешности, допускаемой для данного измерения.

Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности ∆.

 

Качество измерений

Под качеством измерений понимают совокупность свойств, обу­словливающих получение результатов с требуемыми точностными характеристиками, в необходимом виде и установленные сроки.

Качество измерений характеризуется такими показателями, как точность, правильность и достоверность. Эти показатели должны определяться по оценкам, к которым предъявляются требования состоятельности, несмещенности и эффективности.

Истинное значение измеряемой величины отличается от среднего значения на величину систематической погрешности , т. е.

Если систематическая составляющая исключена, то .

Однако из-за ограниченного числа наблюдений Х_ср точно определить также невозможно. Можно лишь оценить это значение, указать границы интервала, в котором оно находится, с определенной вероятностью.

Оценку Х_ср числовой характеристики закона распределения X, изображаемую точкой на числовой оси, называют точечной оценкой. В отличие от числовых характеристик оценки являются случайными величинами. Причем их значение зависит от числа наблюдений п.

Состоятельной называют оценку, которая сводится по веро­ятности к оцениваемой величине, т. е.

Несмещенной является оценка, математическое ожидание которой равно оцениваемой величине, т. е. Х = Х_ср.

Эффективной называют такую оценку, которая имеет наи­меньшую дисперсию

Перечисленным требованиям удовлетворяет среднее арифме­тическое значение результатов п наблюдений.

Результат отдельного измерения является случайной величиной. Тогда точность измерений — это близость результатов измерений к истинному значению измеряемой величины.

Если систематические составляющие погрешности исключить, то точность результата измерений X будет характеризоваться степенью рассеяния его значения, т. е. дисперсией. Как видно из формулы (1.4), дисперсия среднего арифметического значения в n раз меньше дисперсии отдельного результата наблюдения.

На рис. 1.3 заштрихованная площадь определяет плотность вероятности распределения среднего значения.

 

 

 

Правильность измерения определяется приближением значения систематической погрешности к нулю.

Достоверность измерения зависит от степени доверия к результату и характеризуется вероятностью того, что истинное значение измеряемой величины лежит в указанных границах действительного значения.

Эти вероятности называют доверительными вероятностями, а границы (окрестности) — доверительными границами:

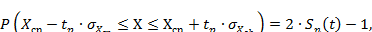
где S_n(t) — интегральная функция распределения Стьюдента. При увеличении числа наблюдений n распределение Стьюдента быстро приближается к нормальному и переходит в него уже при n > 30.

Таким образом, достоверность измерения обусловлена при­ближением к нулю значения случайной (или неисключенной) систематической погрешности.

Для количественной оценки качества измерений рассмотрим влияние параметров измерений на погрешность их результатов.

При планировании измерений и оценке их результатов задают определенную погрешность: предполагают наличие тех или иных составляющих погрешности, закон их распределения, корреляционные (взаимозависимые) связи и др. На основе предположений выбирают средства измерения по точности, необходимый объем выборки объектов измерений и метод оценивания результатов измерений.

Поэтому необходимо знать влияние на погрешность результатов измерений следующих факторов:

· число наблюдений и доверительную вероятность, с которой должны быть известны вероятностные характеристики результатов;

· степень исправленности наблюдений, т. е. наличие неисключенной составляющей погрешности наблюдений, которая образуется из таких составляющих, как метод и сред­ство измерения, неточность изготовления меры и т. д.;

· вид и форма закона распределения погрешностей.

Когда систематические погрешности результатов наблюдений отсутствуют (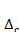 = 0), доверительная погрешность среднего арифметического значения зависит только от погрешности метода , числа наблюдений n и доверительной вероятности Р.

Так как случайная величина имеет распределение Стьюдента с (n - 1) степенями свободы, то, воспользовавшись значениями распределения Стьюдента, можно построить зависимость Такие зависимости для различных значений доверительной вероятности приведены на рис. 1.4.

Как видно из представленных данных, при n < 5 величина существенно зависит от n для любых значений P. При n > 5 зависимость снижается настолько, что возникает задача определения предельного значения числа наблюдений, так как неограниченному уменьшению погрешностей при увеличении n препятствует неисключенная систематическая погрешность.

Дальнейшее увеличение n вызывает незначительное сужение доверительного интервала . Так, если систематические погрешности отсутствуют, то для любого и при п> 7, Р = 0,9, и при п> 8, Р= 0,95, и при п > 10, Р= 0,99 величина уменьшается всего на (6...8) %.

Поэтому при эксплуатации и испытаниях технических средств рекомендуется, во-первых, использовать доверительную вероятность Р = 0,9, так как в этом случае для широкого класса симметричных распределений погрешностей = 1,6 ∙ и не зависит от вида этих распределений, а во-вторых, применять вы­борку наблюдений не более 5.

 

Аналогично ведет себя корреляция результатов измерений параметров изделия. Для выборочного среднеквадратического отклонения среднего арифметического прямого измерения с многократными наблюдениями при условии, что результаты наблюдений и Х_к коррелированы, используется формула

, (1.5)

где — коэффициент корреляции результатов Х₁ и Х_к; К_хх — поправочный множитель.

Формула (1.5) указывает на сильное влияние корреляции результатов наблюдений на (табл. 1.2).

Таблица 1.2. Значения поправочного множителя Кхх в зависимости от коэффициента корреляции при различном числе наблюдений

Коэффициент корреляции	n
0,1	1,1	1,18	1,38	1,7
0,15	1,14	1,25	1,5	1,89
0,25	1,22	1,39	1,74	2,28
0,50	1,41	1,73	2,35	3,24
	1,73	2,24	3,17	4,47

 

Как видно из табл. 1.2, величина может быть существенно занижена. Так, при малой корреляции результатов и п ≤ 20 это занижение не превышает 1,7 раза. При сильной корреляции величина , характеризующая точность результатов измере­ний, может быть занижена в несколько раз.

Заметно влияет на среднеквадратическое отклонение результатов наблюдений , называемое иногда погрешностью мето­да измерений, и степень корректировки результатов наблюдений перед обработкой. Действительно, если выполняются техниче­ские измерения и результат измерения получают в виде среднего арифметического значения Х_ср, то величину погрешности метода в этом случае (обозначим ее ) определяют по формуле (1.2). Если измерения той же величины выполняют с такой точностью, что вместо Х_ср получают истинное значение искомого параметра, т. е. Х_ср = Х, то погрешность метода в этом случае (обозначим ее ) получают по аналогичной формуле, только вмес­то делителя (n - 1) подставляют делитель п.

Несущественная на первый взгляд замена X на Х_ср пораждает ряд проблем. Оказывается, что наиболее употребляемая на практике характеристика как статистическая оценка имеет большее смещение и менее эффективна, чем характеристика .

Для нормального закона распределения погрешностей ошибки в форме среднеквадратического отклонения определяются по формулам

.

При n < 50 величина определяется с ошибками, достигающими десятков процентов. Кроме того, использование вместо приводит к увеличению ошибок оценки на 10 % и более (при n ≤ 3). При n ≤ 10 завышение незначительно.

Оценка качества результатов измерения при недостаточности данных должна быть ориентирована на самый худший случай. Тогда реальное значение будет всегда лучше и получение необходимого результата гарантируется.

Следует отметить, что результаты измерений, не обладающие достоверностью, т. е. степенью уверенности в их правильности, не представляют ценности. Например, датчик измерительной схемы может иметь весьма высокие метрологические характеристики, но влияние погрешностей от его установки, внешних условий, методов регистрации и обработки сигналов приведет к большой конечной погрешности измерений.

Наряду с такими показателями, как точность, достоверность и правильность, качество измерительных операций характеризуется также сходимостью и воспроизводимостью результатов. Эти показатели наиболее распространены при оценке качества испытаний и характеризуют точность испытаний.

Два испытания одного и того же объекта одинаковым методом не дают идентичных результатов. Объективной мерой могут служить статистически обоснованные оценки ожидаемой близости двух или более числа результатов, полученных при строгом соблюдении методики испытаний. В качестве таких статистических оценок согласованности результатов испытаний принимаются сходимость и воспроизводимость.

Сходимость — это близость результатов двух испытаний, полученных одним методом, на идентичных установках и в одной лаборатории.

Воспроизводимость

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: