условие дифракционных минимумов

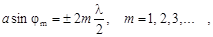(1.21)

 

где φ _m – угол дифракции; m - порядок соответствующего максимума (минимума).

Дифракционная решетка представляет собой систему большого числа N одинаковых по ширине и параллельных друг другу прозрачных щелей шириной а и непрозрачных участков шириной b. Величина

 

d = а + b (1.22)

называется постоянной, или периодом решетки.

Условие главных максимумов при дифракции на решетке

 

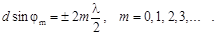(1.23)

 

Условие дополнительных минимумов

 

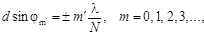(1.24)

 

где m ´ = 1, 2,…, N - 1, N + 1,…; N – полное число штрихов дифракционной решетки. Величина m ´ принимает все целочисленные значения, кроме 0, N, 2 N,…, т.е. кроме тех, при которых условие (1.24) переходит в (1.23).

Разрешающей способностью любого спектрального прибора называется величина

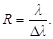(1.24)

 

Здесь Δ λ = λ₁- λ₂ – разрешимый интервал длин волн; λ = (λ₁ + λ₂)/ 2 – середина интервала Δ λ.

Для дифракционной решетки c числом штрихов N в m -ом порядке спектра разрешающая способность равна

 

R = mN. (1.25)

 

При дифракции рентгеновского излучения на пространственной кристаллической решетке условие максимумов имеет вид

 

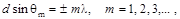(1.26)

 

где d - расстояние между атомными плоскостями кристалла; θ _m – угол между направлением падающего излучения и гранью кристалла, называемый углом скольжения. Последнее выражение называется формулой Вульфа - Брэгга.

ПРИМЕР. На щель шириной а = 0,1 мм нормально падает параллельный пучок монохроматического света длины волны λ = 500 нм. Дифракционная картина наблюдается на экране, расположенном на расстоянии L от щели. Ширина изображения щели b на экране составляет 1 см. Найти величину L.

 

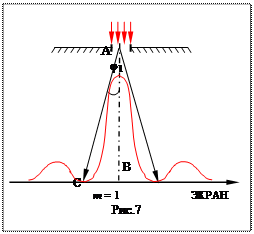
РЕШЕНИЕ. Шириной изображения щели считается расстояние между первыми минимумами (рис.7). Угол φ₁ показывает направление на первый дифракционный минимум, условие которого согласно (1.21) можно записать

 

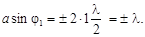(1.27)

Величину L можно определить из прямоугольного треугольника АВС из соотношения

tg φ₁ = b /2L,

 

заменяя tg φ₁ на sin φ₁, что возможно при малых углах:

 

L = b /2 sin φ₁

 

Используя соотношение (1.27), окончательно получим

 

L = bа /2 λ.

 

Подставим в численный расчет все величины в системе СИ:

 

0,1∙10^-3∙1∙10^-2

L = ––––––––-––– = 1 (м).

2∙5∙10^-7

 

ПРИМЕР. Постоянная дифракционной решетки 10 мкм, ее ширина 2 см. В спектре какого порядка эта решетка может разрешить дублет λ₁ = 486,0 нм и λ₂ = 486,1 нм?

 

РЕШЕНИЕ. Разрешающая способность дифракционной решетки

λ

R = ––- = mN,

Δ λ

 

где Δ λ — минимальная разность длин волн двух спектральных линий λ и λ + Δ λ, разрешаемых решеткой; т — порядок спектра; N — число щелей решетки.

Поскольку постоянная решетки d есть расстояние между сере­динами соседних щелей, общее число щелей можно найти как

 

N = l / d,

где l — ширина решетки.

Из этих двух формул находим:

λ d λ

Δλ = ––––– = ––––.

mN ml

 

Дублет спектральных линий λ₁ и λ₂ будет разрешен, если

 

Δ λ ≤ λ₂ - λ₁.

 

Учитывая, что λ = (λ₁ + λ₂ )/2 получим

 

d (λ₁ + λ₂ )

––––––––- ≤ λ₂ - λ₁,

2 ml

откуда следует, что дублет λ₁ и λ₂ будет разрешен во всех спектрах с порядком

d (λ₁ + λ₂ )

m ≥ ––––––––––-.

2 l (λ₂ - λ₁ )

 

Подставляя числовые данные, получим

 

10 ·10 ^-6 м · (486,0· + 486,1)10 ^-9 м

m ≥ ––––––––––––––––––––––––––––––––– = 2,43.

2·10 ^-6 м (486,1-486,0) 10 ^-9 м

 

Так как т — целое число, то т ≥ 3.

1.5. ПОЛЯРИЗАЦИЯ СВЕТА

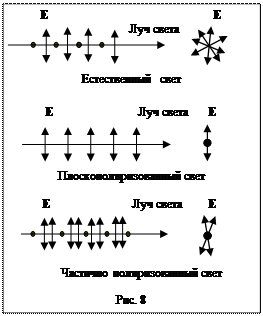Поляризованным называется свет, в котором колебания вектора напряженности электрического поля Е (светового вектора), упорядочены каким либо образом. Если световой вектор электромагнитной волны колеблется в определенной плоскости, его можно назвать плоскополяризованным., или неполяризованный свет имеет всевозможные направления колебания вектора Е. Световой вектор при этом всегда перпендикулярен направлению распространения световой волны, поэтому можно сказать, что электромагнитные волны поперечно поляризованы. На рис.8 показано, как изображаются волны различной поляризации.

Устройства, позволяющие получить плоскополяризованный свет, называются поляризаторами.

Закон Малюса для плоскополяризованного света имеет вид

 

I = I ₀ cos² α, (1.27)

 

где I ₀ и I — интенсивность плоско­поляризованного света, па­дающего и прошед­шего че­рез идеальный поляризатор; α — угол между плос­костью по­ляризации падающего све­та и главной плоскостью поляризатора.

Если через поляризатор пропускать естественный свет, то угол α будет быстро и беспорядочно принимать с равной вероятностью все значения от 0 до 90˚, и интенсивность света, прошедшего через поляризатор

 

I = I ₀ <cos² α> = 0,5 I _0, (1.28)

 

где <cos² α> = 0,5 – среднее значение cos² α за достаточно большой промежуток времени.

Закон Брюстера 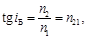(1.29)

где i _Б — угол Брюстера, при котором отраженный от поверхности диэлектрика свет полностью поляризован; n ₁ и n ₂ — показатели преломле­ний первой и второй сред.

Вещества, вращающие плоскость поляризации световой волны, называются оптически активными.

Угол поворота плоскости поляризации оптически активными кристаллами и чистыми жидкостями

φ = α d, (1.30)

 

оптически активными растворами

φ = [α] d C, (1.31)

 

где d – толщина слоя оптически активного вещества; С - его массовая концентрация.

Некоторые прозрачные кристаллы, являясь анизотропными веществами, обладают свойством двойного лучепреломления, т. е. при попадании на него луч света раздваивается на два луча – обыкновенный (о) и необыкновенный (е) с разными свойствами. У них разные законы преломления и показатели преломления n _о и n _е , взаимно перпендикулярная поляризация.

Двойное лучепреломление может возникать и в изотропных телах, которые становятся анизотропными под воздействием электрического поля напряженности Е (эффект Керра). Разность показателей преломления обыкновенного и необыкновенного лучей в этом случае

n _о- n _е = k Е ², (1.32)

 

где k - постоянная Керра данного материала.

 

ПРИМЕР. Естественный свет проходит через систему из трех одинаковых поляроидов, в каждом которых из-за отражения и поглощения света теряется 20% падающего на него излучения. Плоскости поляризации первого и второго поляроидов составляют угол α ₁ = 30˚, а первого и третьего – 90˚ (рис.9). Во сколько раз уменьшится интенсивность света, вышедшего из этой системы?

 

РЕШЕНИЕ. Обозначим интенсивности естественного света, падающего на первый поляризатор П₁ через а I ₀, вышедшего из первого, второго и третьего поляроидов – I ₁, I ₂и I ₃ соответственно. Пластинками П₁, П₁, П ₃ изобразим поляроиды, пунктирными прямыми ОО₁, ОО₂ , ОО₃ укажем положение их плоскостей поляризации. После прохождения каждого из поляризаторов колебания светового вектора Е будет происходить параллельно ОО₁, ОО₂ , ОО₃. Рассмотрим прохождение света последовательно через каждый поляроид. Если бы поляроиды были идеальными, то интенсивности света, проходящего через них, можно было определить по формулам (1.28) и (1.27). С учетом 20% потерь запишем:

 

 

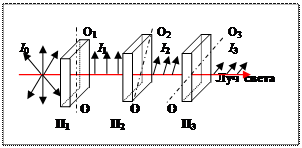
I ₁ = 0,5 I ₀ (1- 0,2);

 

I ₂ = I ₁ cos² α₁(1- 0,2) = 0,5 I ₀ (1- 0,2)²;

 

I ₃ = I ₂ cos² (α₂ -α₁) (1- 0,2) = 0,5 I ₀ (1- 0,2)³.

 

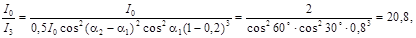Тогда

т.е. интенсивность вышедшего света уменьшится в 20,8 раз.

 

ПРИМЕР. Определить показатель преломления прозрачного вещества, если угол Брюстера при падении на него света из воздуха оказался равным предельному углу.

РЕШЕНИЕ. Обозначим искомый показатель преломления n _х, показатель преломления воздуха n ₁. Закон Брюстера (1.29) запишем в виде

 

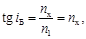(1.33)

т.к. для воздуха n ₁ = 1.

Полное внутреннее отражение имеет место при переходе светового луча из неизвестной прозрачной среды в воздух. Используем закон преломления света (1.3) с учетом, что β = 90˚ и sin 90˚= 1

 

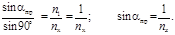(1.34)

 

Преобразуем формулу (1.33) следующим образом:

 

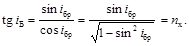(1.35)

 

Учитывая, что по условию задачи i _бр = α_пр, имеем

 

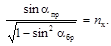(1.36)

 

Подставив вместо sin α_пр величину 1/ n _х, согласно уравнению (1.34), получим

 

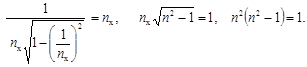(1.37)

 

Произведем замену переменных n _x² = t. Тогда последнее уравнение (1.37) примет вид

t ² - t - 1= 0.

Оно имеет два решения:

 

 

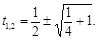
Исходя из физического смысла, выберем решение

 

 

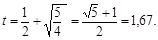
Тогда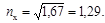

 

1.6. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

С ВЕЩЕСТВОМ

Дисперсией света называется явлениезависимость показателя преломления вещества от длины волны (или частоты) падающего излучения.

Качественной характеристикой этого явления служит производная от показателя преломления по длине волны, называемая дисперсией вещества D:

d n

D = –––. (1.38)

d λ

 

При нормальной дисперсии показатель преломления вещества уменьшается с увеличением длины волны, и d n / d λ < 0. Это имеет место для всех прозрачных бесцветных материалов.

При аномальной дисперсии показатель преломления увеличивается с увеличением длины волны и d n / d λ > 0. Этот случай наблюдается вблизи полос поглощения света.

Согласно молекулярной теории дисперсии света вдали от областей поглощения света

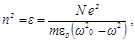(1.39)

 

где ε – диэлектрическая постоянная вещества; ω ₀ – собственная частота колебаний молекул; ω – частота падающего излучения; m и e – масса и заряд электрона.

Строго монохроматическая волна распространяется со скоростью

 

ω λ λ с

v = ω / k = -––- = ν λ = ––- = –––-, (1.40)

2π Т n

 

которая называется фазовой скоростью. Здесь λ – длина волны; k = 2π /λ –волновое число (измеряется в 1/м, м^-1); Т - период колебаний; с – скорость волны в вакууме.

Пакет (группа) волн в диспергирующей среде распространяется с групповой скоростью

d ω

u = –––-. (1.41)

d k

Связь междуфазовой и групповой скоростями описывается формулой Рэлея

dvdv

u = v + k –––- = v - k –––-. (1.42)

d k d λ

 

Из этой формулы видно, что в зависимости от знака dv/d λ групповая скорость может быть как больше, так и меньше фазовой скорости. В недеспергирующей среде dv/dλ =0, и обе скорости совпадают.

 

ПРИМЕР. Показатели преломления дистиллированной воды для света длин волн λ₁ = 486 нм и λ₂ = 509 н соответственно равны n ₁= 1,3371 и n ₂ = 1, 3360. Определить средние значения фазовой и групповой скоростей в этом интервале длин волн.

 

РЕШЕНИЕ. Считая, что показатель преломления в заданном интервале длин волн изменяется линейно, среднюю фазовую скорость v определим как среднюю арифметическую скоростей v₁ и v₂, которые найдем из соотношений v₁ = с / n ₁ и v₂= с / n _2, где с – скорость света в вакууме.

 

v₁ + v₂ с 1 1 3∙10⁸ 1 1

<v> = ––––––- = –– (–- + ––-) = –––– (–––––- + ––––––-) = 1,24∙10⁸ м/с.

2 2 n ₁ n ₂ 2 1,3371 1, 3360

 

При определении групповой скорости заменим производную dv/dλ приращениями Δv/Δλ, что вполне обоснованно при малых интервалах Δv и Δλ, как в нашей задаче. Тогда средняя групповая скорость будет равна

 

 

 

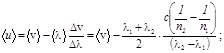
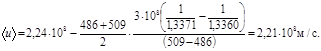
Отметим, что групповая скорость в данной задаче меньше фазовой, т.е. мы находимся в области нормальной дисперсии. Это следует и из условия задачи, поскольку показатель преломления воды уменьшается с увеличением длины волны.

При прохождении света через поглощающее вещество интенсивность света ослабляется по закону Бугера

 

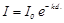(1.43)

Здесь I₀, I – интенсивности света на входе и выходе из поглощающего слоя толщиной d; k – коэффициент поглощения излучения (измеряется в 1/м, м^-1); е – основание натурального логарифма, е = 2,72. Для растворов k = βс, где с – концентрация растворенного вещества; β – коэффициент поглощения на единицу концентрации вещества.

 

ПРИМЕР. Пучок монохроматического света поочередно пропускают через две пластинки толщиной d = 1 см. Коэффициент поглощения первой пластинки в 4 раза меньше коэффициента поглощения второй. Интенсивность света на выходе из второй пластинки в 3 раза меньше, чем из первой. Коэффициенты отражения света от поверхностей пластинок одинаковы. Определить коэффициенты поглощения k ₁ и k ₂ обеих пластинок.

 

РЕШЕНИЕ. Пусть интенсивность света, падающего на пластинки I₀, коэффициент отражения света каждой пластинки r. Тогда из первой пластины выйдет свет интенсивности

 

 

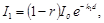
из второй-

 

 

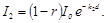
Учитывая, что k ₂= 4 k ₁, найдем отношение интенсивностей

 

 

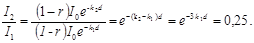
Прологарифмируем правую и левую части последнего выражения:

 

 

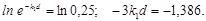
Подставим числовые значения и определим k ₁ и k ₂:

 

 

 

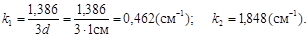
1.7. ФОТОНЫ

Согласно квантовой теории свет может испускаться и поглощаться только порциями (квантами). Энергия кванта света, или фотона определяется как

 

ε = hν = ћω = hc /λ, (1.44)

где h= 6,63∙10^-34 Дж∙с, ћ = h /2π = 1,02∙10^-34 Дж∙с – постоянные Планка; ν и ω – частоты и циклическая частоты излучения; – длина волны излучения; с = 3∙10⁸ м/с – скорость света в вакууме.

 

Импульс фотона

р = mc = ε / c = hν / с = ћω/с =h / λ. (1.45)

 

При соударении с поверхностью фотоны передают ей импульс, вследствие чего возникает световое давление Р. При нормальном падении светового потока на поверхность с коэффициентом отражения давление света равно

Е _е

Р = ––––(1 + ρ) или Р = ω (1 + ρ), (1.46)

с

где Е _е = W / St = Nhν / St – облученность поверхности, т.е. энергия всех N фотонов, падающих в единицу времени на поверхность площадью S; – объемная плотность энергии излучения.

 

1.8. ВНЕШНИЙ ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ

 

Внешнимфотоэлектрическим эффектом (фотоэффектом) называется явление испускания электронов металлами под действием света вследствие чего можно получить электрический ток. Сущность фотоэффекта объясняется квантовой теорией излучения.

При взаимодействии с электроном падающий фотон передает ему всю энергию, которая расходуется электроном на совершение работы выхода А _вых за пределы вещества, т.е. на преодоление потенциального барьера металл - вакуум, и на приобретение им кинетической энергии W _max. Энергетический баланс при фотоэффекте выражается уравнением Эйнштейна:

 

hν = А _вых + W _max, (1.47)

 

Если фотоэффект вызван фотоном, имеющим небольшую энергию (hν < 0,51 МэВ), то кинетическую энергию можно рассчитать по классической формуле

m ₀v² _max

W _max = –––––––, (1.48)

где m ₀ – масса покоя электрона; ₀ v _max - максимальная скорость выбиваемых электронов.

Если фотоэффект вызывается фотоном большой энергии (hν > 0,51 МэВ) вычисление энергии W _max проводится по релятивистской формуле

 

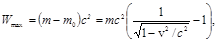(1.49)

 

m – масса релятивистского электрона.

Из уравнения Эйнштейна следует возможность фотоэффекта при условии, что энергии фотона должно хватать по меньшей мере на отрыв электрона от металла, не сообщая ему скорости (v_max = 0). Из уравнения (1.47) при этом условии имеем

 

hν ₀ = hс / λ₀ = А _вых, (1.50)

 

где ν ₀ и λ₀ называются "красной" границей фотоэффекта. Из последнего выражения следует, что "красная" граница фотоэффекта

 

ν₀ = А _вых/ h.; λ₀= hс / А _вых, (1.51)

 

зависит только от работы выхода электрона из металла А_вых, а значит от природы металла и состояния его поверхности.

Фототок прекращается, если

 

W _max = eU _зад. (1.52)

 

Здесь U _зад – задерживающее напряжение внешнего электрического поля.

 

ПРИМЕР. Цезиевая пластинка освещается монохроматическим светом длины волны λ = 430 нм. Определить максимальную скорость выбиваемых фотоэлектронов и наименьшее задерживающее напряжение, при котором фототок прекращается.

 

РЕШЕНИЕ. Сначала определим фотона падающего излучения:

 

hc 6,63∙10^-34 Дж∙с∙3∙10⁸ м/с

ε = ––––– = ––––––––––––––––––––- = 4,97∙10^-19Дж =

λ 430∙10^-9 м

 

4,97∙10^-19Дж

= –––––––––––– = 3,1 (эВ).

1,6∙10^-19

 

Как видим, эта энергия намного меньше 0,51 МэВ, т.е. для вычисления кинетической энергии фотоэлектрона можно пользоваться классической формулой (1.48).

Запишем уравнение Эйнштейна (1.47) в виде

c m ₀v² _max

h --- = А _вых + –––––––.

λ 2

Из табличных данных находим "красную" границу для цезия:

 

λ₀ = 640 нм.

 

Согласно (1.51) работа выхода для цезия

 

А _вых = hс / λ₀.

 

Тогда максимальная скорость выбиваемых электронов

 

 

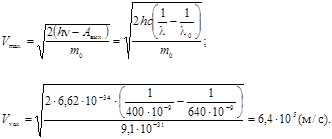
Задерживающее напряжение находим из условия

 

 

 

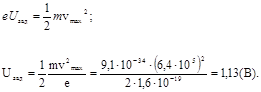
1.9. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ

Испусканиеэлектромагнитных волн за счет внутренней энергии тела называется тепловым излучением. Оно возникает всегда при температуре выше 0 К, поэтому испускается всеми телами, но далеко не всегда воспринимается глазом как свечение. Если объект полностью поглощает падающее излучение всех длин волн, ничего не отражая, то его называют абсолютно черным телом. Поглощательная способность таких тел а _λ,Т равна единице. Для так называемых “серых” тел а _λ,Т < 1

Нагретое тело излучает электромагнитные волны различных длин волн. Спектральной плотностью энергетической светимости называется величина r(λ), равная отношению мощности излучения единицы поверхности нагретого тела в спектральном диапазоне dλ. Пользуясь квантовыми представлениями М. Планк получил зависимость спектральной плотности энергетической светимости черного тела зависит от длины волны r (λ,Т) (или частоты излучения r (ν,Т) и температуры в следующем виде:

 

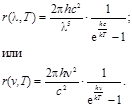(1.53)

 

Из последних соотношений следует закон Стефана-Больцмана для абсолютно черных тел, чаще всего применяемый для решения практических задач:

 

R = σ T ⁴, (1.54)

 

где R = W / St = N / S называется интегральной светимостью нагретого тела при термодинамической температуре Т, измеряемой в системе единиц СИ в кельвинах (К); W и N -- соответственно энергия и мощность, излучаемые нагретой поверхностью площадью S за время t; σ = 5,67 ∙10^-8 Вт/м²∙ К⁴ - постоянная Стефана-Больцмана.

Для “ серых ” тел закон Стефана-Больцмана имеет вид

 

R = а _λ,Т∙σ T ⁴. (1.55)

 

Два закона Вина также являются следствием формул Планка (1.53).

Первый закон (закон смещения) Вина:

 

λ_max = b / T, (1.56)

 

где λ_max -- длина волны, на которую приходится максимум спектральной плотности энергетической светимости черного тела; b = 2,89∙10^-3 м∙К -- постоянная Вина. Этот закон выполняется и для “ серых ” тел.

Второй закон Вина:

 

r (λ,Т)_мах = с´ / Т ⁵, (1.57)

 

r (λ,Т)_мах - максимальное значение спектральной плотности энергетической светимости черного тела; постоянная с´ = 1,30∙10^-5 Вт/(м²∙К⁵ ).

 

ПРИМЕР. Муфельная печь потребляет мощность N ₀ = 1 КВт. Температура Т внутренней поверхности печи при открытой дверце площадью S = 25см² равна 1200 К. Считая, что через открытую дверцу печь излучает как абсолютно черное тело, определить, какая часть ее мощности рассеивается стенками печи. Какова частота излучения, соответствующая максимуму излучательной способности печи?

 

РЕШЕНИЕ. Определим мощность излучения N через открытую дверцу печи из выражения (1.54):

N = R S = σ T ⁴ S;

N = 5,67 ∙10^-8 Вт/м²∙ К⁴ ∙(1200К)⁴∙2510^-4 м² = 293,9 Вт.

 

Потери мощности за счет рассеивания тепла стенками печи

Δ N = N - N ₀.

 

Доля рассеиваемой мощности

Δ N / N ₀= (N - N ₀)/ N ₀;

 

Δ N / N ₀ = (1000 Вт - 293,9 Вт)/ 1000 Вт = 708,1/1000 = 0,71 = 71 %

 

Частота излучения, соответствующая максимуму излучательной способности печи

 

ν _мах = с / λ _мах (с - скорость света в вакууме)

 

или с использованием закона смещения Вина (1.56)

 

ν _мах= с T / b;

 

ν _мах= 3 ∙10⁸⁽м/с) ∙1200/2,89∙10^-3 м∙К = 12,5∙10¹³ Гц.

 

 

ЭФФЕКТ КОМПТОНА

Суть этого явления заключается в изменении длины волны рентгеновского излучения при его рассеянии на свободных электронах (или других частицах) вещества:

h

Δλ = λ´ - λ = ----- (1 - cosθ) = λ_c(1- cosθ) = λ_c sin ²θ. (1.58)

m ₀ c

 

Здесь λ и λ´ - длины волн падающего и рассеянного излучений; Δλ - изменении длины волны при эффекте Комптона; θ- угол рассеяния фотона; m - масса покоя электрона (либо другой частицы); h - постоянная Планка; с - скорость света в вакууме; λ_c = h/ m ₀ c - так называемая комптоновская длина волны, равная 2,43 пм при рассеянии излучения на электронах. Эффект Комптона является ярким примером корпускулярных свойств электромагнитного излучения.

 

ПРИМЕР. Фотон с энергией ε = 0,750 МэВ рассеялся на свободном электроне под углом 60˚. Принимая, что кинетическая энергия и импульс электрона до соударения с фотоном были пренебрежимо малы, определить:

1) энергию рассеянного фотона ε´;

2) кинетическую энергию W _e и направление движения электрона отдачи.

 

РЕШЕНИЕ. Ввиду громоздкости математических преобразований данную задачу удобнее решать не в общем виде, а с промежуточными вычислениями.

1) Найдем длину волны падающего излучения, зная его энергию:

 

hс 6,63∙10^-34 Дж∙с∙3 ∙10⁸ м/с

λ = -----; λ = --------------------------------- = 1,675∙10^-12м = 1,675 пм.

ε 0,750∙10⁶∙1,6∙10^-19Дж

 

По формуле Комптона (1.58) вычислим разность длин волн после и до рассеяния:

Δλ = λ´ - λ = λ_c(1- cos60˚);

 

Δλ = 2,43(1 - 0,5) = 1,215 пм.

 

Отсюда следует, что длина волны рассеянного излучения

 

λ´ = λ + Δλ; λ´ = 1,675 пм +1,215 пм = 2,890 пм = 2,890∙10^-12 м.

 

Тогда энергия рассеянного фотона

hс 6,63∙10^-34 Дж∙с∙3 ∙10⁸ м/с

ε´ = -----; ε´ = --------------------------------- = 6,918∙10^-14 Дж =0,433 МэВ.

λ´ 2,890∙10^-12 м

 

2) Кинетическая энергия электрона отдачи согласно закону сохранения энергии равна разности энергий падающего и рассеянного фотона:

 

W _e= ε - ε´; W _e=0,750 МэВ - 0,433 МэВ = 0,317 МэВ = 0,507∙10^-13Дж.

 

Направление движения электрона отдачи найдем, применяя закон сохранения импульса для системы фотон - электрон:

 

р = р´ + р _е,

 

где р - импульс падающего фотона (импульс свободного электрона до столкновения равен 0); р´ и р _е- импульсы рассеянного фотона и электрона отдачи после столкновения. Векторная диаграмма импульсов изображена на рис. 9.

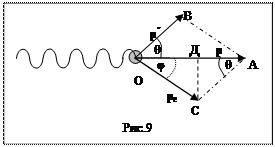Все вектора проведены из точки О, где находился электрон в момент соударения с фотоном. Угол φ определяет направление движения электрона отдачи. Из треугольника ОСД находим

 

СД

tg φ = ------- =

ОД

 

СА∙ sin θ

= ---------------------

ОА - СА∙cos θ

 

 

р ´ sin θ sin θ

или tg φ = --------------- = -----------------.

р - р ´ cos θ р / р ´ - cos θ

 

Так как р = ε / с и р ´= ε ´/ с, то

sin θ 0,866

tg φ = ---------------; tg φ = --------------------- = 0,703.

ε / ε ´ - cos θ 0,750/0,433 - 0,5

 

Отсюда следует, что угол φ ≈ 35˚.

 

Поделиться:

Воспользуйтесь поиском по сайту: