 |
Сложение ускорений в общем случае переносного движения
|
|
|
|
Лекция 9
Краткое содержание: Сложное движение точки в общем случае: абсолютная и относительная производные, сложение скоростей, сложение ускорений. Ускорение Кориолиса. Правило Жуковского.
Сложное движение точки в общем случае
Абсолютная и относительная производные
При рассмотрении сложного движения точки необходимо рассматривать изменение векторных величин с течением времени по отношению к системам отсчета, движущимся друг относительно друга.
Рассмотрим произвольный вектор 
в двух системах отсчета: подвижной и неподвижной. В подвижной системе отсчета только проекции вектора 
являются функциями времени, в неподвижной системе отсчета кроме проекций, функциями времени являются и единичные вектора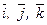 
(они изменяют свое направление в пространстве).
(9-1)
Рис. 9-1
Введем обозначения 
- абсолютная производная – производная в неподвижной системе отсчета; 
- относительная производная – производная в подвижной системе отсчета.
Установим зависимость между абсолютной и относительной производными. Вычислим абсолютную производную по времени от вектора используя формулу (9-1). Получим
(9-2)
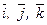Первые три слагаемых учитывают изменение вектора при неизменных и поэтому составляют относительную производную, т.е.
. (9-3)
Производные по времени от единичных векторов определим по формулам Пуассона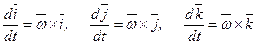 
Вектор 
- это угловая скорость вращательной части движения вокруг точки О подвижной системы отсчета относительно неподвижной.
После подстановки получаем
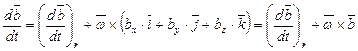. (9-4)
Получена формула зависимости производных вектора в двух системах отсчета движущихся друг относительно друга (формула Бура).
Сложение скоростей
|
|
|
Пусть система отсчета O 1 x 1 y 1 z 1 - неподвижная, а система отсчета Oxyz - подвижная. Движение точки относительно основной неподвижной системы отсчета O 1 x 1 y 1 z 1 называется абсолютным. Движение точки относительно подвижной системы отсчета Oxyz называется относительным.Переносным движением точки называется движение, которое она совершает вместе с подвижной системой отсчета, как точка, жестко скрепленная с этой системой в рассматриваемый момент времени. Относительные скорость и ускорение обозначают 
и 
, переносные - 
и 
, а абсолютные - 
и 
.
Рис. 9-2
Движение подвижной системы отсчета относительно неподвижной можно охарактеризовать скоростью ее поступательного движения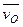 
, например вместе с точкой О, и вектором угловой скорости ее вращения вокруг О.
Теорема. Скорость абсолютного движения точки равна векторной сумме переносной и относительной скоростей. 
Доказательство. Рассмотрим движение точки 
. Положение точки относительно неподвижной системы отсчета определяется вектором 
, а относительно подвижной вектором 
. Положение точки 
относительно неподвижной системы отсчета определяется вектором 
. Для любого момента времени выполняется тождество 
.
Продифференцируем его по времени (вычислим производные в неподвижной системе отсчета) и получим
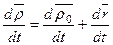(9-5)
По определению, 
- абсолютная скорость точки , 
- абсолютная скорость точки . Для вычисления 
применим формулу Бура. Имеем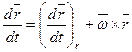 
. Относительная производная 
- является относительной скоростью точки по отношению к неподвижной системе отсчета, а - угловая скорость вращения подвижной системы отсчета.
Таким образом из (9-5) получаем
(9-6)
Скорость
является скоростью точки свободного твердого тела, скрепленного с подвижной системой координат, с которой в данный момент совпадает точка в движении тела относительно неподвижной системы отсчета. Это есть переносная скорость точки .
|
|
|
Окончательно получаем
, (9-7)
что и требовалось доказать.
Сложение ускорений в общем случае переносного движения
Теорема. (кинематическая теорема Колиолиса) Абсолютное ускорение точки является векторной суммой трех ускорений - переносного, относительного и Кориолиса. 
Доказательство. Абсолютное ускорение точки определим вычислением полной производной по времени от абсолютной скорости.
Для производных от векторов и 
применим формулу Бура. Получим
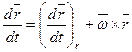
Учитывая, что 
, 
, , 
,
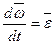получим для абсолютного ускорения
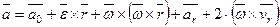(9-8)
В этой формуле первые три слагаемых являются переносным ускорением для точки 
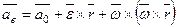. Последнее слагаемое называется ускорением Кориолиса (иногда его называют добавочным или поворотным ускорением) и обозначается 
.
В итоге формула (9-8) принимает вид
, (9-9)
что и требовалось доказать.
Ускорение Кориолиса
Теорема (Правило Жуковского). Модуль ускорения Кориолиса равен удвоенному произведению угловой скорости переносного вращения на модуль проекции относительной скорости на плоскость, перпендикулярную оси переносного вращения; чтобы получить направление ускорения Кориолиса, необходимо вектор проекции относительной скорости повернуть на 
вокруг оси, параллельной оси переносного вращения в направлении этого вращения.
|
|
|
