 |
Задания для самостоятельной работы.
|
|
|
|
ЕН 01 МАТЕМАТИКА
Сборник заданий для внеаудиторной самостоятельной работы по теме: «Применение дифференциала к приближенным вычислениям».
для специальностей:
08.02.01 Строительство и эксплуатация зданий и сооружений
08.02.05 Строительство и эксплуатация автомобильных дорог и аэродромов
21.02.04 Землеустройство
Вологда 2015
Математика: Сборник заданий для внеаудиторной самостоятельной работы по теме: «Применение дифференциала к приближенным вычислениям» для специальностей: 08.02.01 Строительство и эксплуатация зданий и сооружений, 08.02.05 Строительство и эксплуатация автомобильных дорог и аэродромов, 21.02.04 Землеустройство.
Данный сборник заданий для внеаудиторной самостоятельной работы по теме: «Применение дифференциала к приближенным вычислениям» представляет собой учебно-методическое пособие по организации самостоятельной внеаудиторной работы студентов.
Содержит задания для самостоятельной внеаудиторной работы для шести вариантов и критерии оценки выполнения самостоятельной работы.
Комплект призван помочь студентам систематизировать и закрепить полученные на аудиторных занятиях по математике теоретический материал, сформировать практические навыки.
Составитель: Е. А. Севалёва – преподаватель БПОУ ВО «Вологодский строительный колледж»
Рецензент: А. Л. Савельева – преподаватель БПОУ ВО «Вологодский индустриально – транспортный техникум»
Содержание.
1. Пояснительная записка.
2. Самостоятельная работа.
3. Критерии оценки.
4. Литература.
Пояснительная записка
Данная работа представляет собой учебно-методическое пособие по организации самостоятельной внеаудиторной работы студентов по дисциплине ЕН 01 «Математика» для специальностей 08.02.01 Строительство и эксплуатация зданий и сооружений, 08.02.05 Строительство и эксплуатация автомобильных дорог и аэродромов, 21.02.04 Землеустройство.
|
|
|
Цель методических указаний состоит в обеспечении эффективности самостоятельной работы, определении ее содержания, установления требований к оформлению и результатам самостоятельной работы.
Целями самостоятельной работы студентов по дисциплине ЕН 01 «Математика: алгебра и начала математического анализа, геометрия» являются:
· систематизации и закрепления полученных теоретических знаний и практических навыков;
· углубление и расширение теоретических знаний;
· формирование умений использовать справочную и дополнительную литературу;
· развитие познавательных способностей и активности студентов, творческой инициативы, самостоятельности и самоорганизации;
· активизации учебно-познавательной деятельности будущих специалистов.
Самостоятельные работы выполняются индивидуально в свободное от занятий время.
Студент обязан:
- перед выполнением самостоятельной работы, повторить теоретический материал, пройденный на аудиторных занятиях;
- выполнить работу согласно заданию;
- по каждой самостоятельной работе представить преподавателю отчет в виде письменной работы.
Самостоятельная работа по теме:
«Применение дифференциала к приближенным вычислениям»
Цель: закрепить навык вычисления приближённого значения функции с помощью дифференциала.
Теория.
Приращение  функции
функции  представимо в виде:
представимо в виде:
 ,
,
где функция 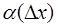 является бесконечно маленькой функцией при стремлении аргумента
является бесконечно маленькой функцией при стремлении аргумента  к нулю.
к нулю.
Так как  , то
, то 
В силу того, что второе слагаемое 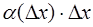 является бесконечно малым, то им можно пренебречь, а поэтому
является бесконечно малым, то им можно пренебречь, а поэтому 
А так как в нахождении дифференциал значительно проще, чем приращение функции, то данная формула активно используется на практике.
|
|
|
Для приближенного вычисления значения функции применяется следующая формула:  .
.
Пример 1. Вычислить приближенно  , заменяя приращение функции ее дифференциалом.
, заменяя приращение функции ее дифференциалом.
Решение:
· Рассмотрим функцию  . Необходимо вычислить ее значение в точке
. Необходимо вычислить ее значение в точке 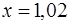 .
.
· Для приближенного вычисления значения функции применяется следующая формула:  .
.
· Величину х представим в виде  , т. е.
, т. е.  , тогда
, тогда  ,
,  .
.
· Вычислим значение функции  в точке
в точке  :
:  .
.
· Продифференцируем рассматриваемую функцию:  .
.
· Найдем значение  :
: 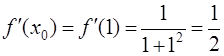 .
.
· Итак, 
 .
.
Ответ.  .
.
Пример 2. С помощью дифференциала вычислить приближенно  .
.
Решение:
· Рассмотрим функцию  . Необходимо вычислить ее значение в точке
. Необходимо вычислить ее значение в точке  .
.
· Для приближенного вычисления значения функции применяется следующая формула:  .
.
· Величину х представим в виде  , т. е.
, т. е. 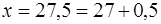 , тогда
, тогда  ,
, 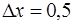 .
.
· Вычислим значение функции  в точке
в точке  :
:
 .
.
· Продифференцируем рассматриваемую функцию: 
· Найдем значение  :
:  .
.
· Подставляя все в формулу, окончательно получим: 
Ответ. 
Пример 3. С помощью дифференциала вычислить приближенно  .
.
Решение:
· Рассмотрим функцию  . Необходимо вычислить ее значение в точке
. Необходимо вычислить ее значение в точке  .
.
· Для приближенного вычисления значения функции применяется следующая формула:  .
.
· Величину х представим в виде  , т. е.
, т. е.  , тогда
, тогда  ,
,  .
.
· Вычислим значение функции  в точке
в точке  :
:
 .
.
· Продифференцируем рассматриваемую функцию:  .
.
· Найдем значение  :
:  .
.
· Подставляя все в формулу, окончательно получим: 
Ответ. 
Пример 4. С помощью дифференциала вычислить приближенно  .
.
Решение:
· Рассмотрим функцию 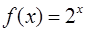 . Необходимо вычислить ее значение в точке
. Необходимо вычислить ее значение в точке  .
.
· Для приближенного вычисления значения функции применяется следующая формула:  .
.
· Величину х представим в виде  , т. е.
, т. е. 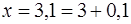 , тогда
, тогда  ,
,  .
.
· Вычислим значение функции 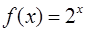 в точке
в точке  :
:
 .
.
· Продифференцируем рассматриваемую функцию: 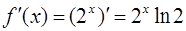 .
.
· Найдем значение  :
:  .
.
· Подставляя все в формулу, окончательно получим: 
Ответ. 
Пример 5. С помощью дифференциала вычислить приближенно  .
.
Решение:
· Рассмотрим функцию  . Необходимо вычислить ее значение в точке
. Необходимо вычислить ее значение в точке  .
.
· Для приближенного вычисления значения функции применяется следующая формула:  .
.
· Величину х представим в виде  , т. е.
, т. е. 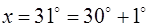 , тогда
, тогда 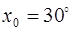 ,
, 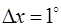 .
.
· Переведём градусы в радианы:  ,
, 
· Вычислим значение функции  в точке
в точке 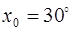 :
:
|
|
|
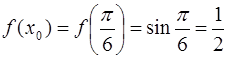 .
.
· Продифференцируем рассматриваемую функцию:  .
.
· Найдем значение  :
: 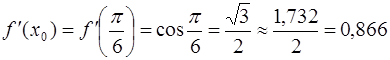
· Подставляя все в формулу, окончательно получим: 
Ответ. 
Задания для самостоятельной работы.
| 1 вариант | 2 вариант | 3 вариант |
С помощью дифференциала вычислить приближенно:
1.  ;
2. ;
2. 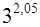 ;
3. ;
3. 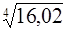 ;
4. ;
4.  . .
| С помощью дифференциала вычислить приближенно:
1.  ;
2. ;
2.  ;
3. ;
3.  ;
4. ;
4.  . .
| С помощью дифференциала вычислить приближенно:
1.  ;
2. ;
2. 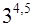 ;
3. ;
3.  ;
4. ;
4.  . .
|
| 4 вариант | 5 вариант | 6 вариант |
С помощью дифференциала вычислить приближенно:
1. 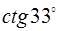 ;
2. ;
2.  ;
3. ;
3.  ;
4. ;
4.  . .
| С помощью дифференциала вычислить приближенно:
1.  ;
2. ;
2. 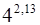 ;
3. ;
3.  ;
4. ;
4. 
| С помощью дифференциала вычислить приближенно:
1.  ;
2. ;
2.  ;
3. ;
3. 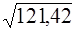 ;
4. ;
4. 
|
|
|
|


