 |
Метод декомпозиции (рационализации)
|
|
|
|
Метод рационализации
Составитель текста – Прокофьева Т.А. (МБОУ СШ №12)
Как известно, ЕГЭ по Математике длится 235 минут, и чтобы распределить это время рационально на все задания, не помешало бы узнать короткие пути решения той или иной задачи. Так, на С3(задача №15), оцениваемое в 3 балла, рекомендовано 30 минут (при условии, что ученик намерен решать все задания). Если проводить решение согласно всем известному методу интервалов, то, возможно, вы потратите все отведенное на него время. Существует ли такой метод решения неравенств, при котором мы сможем упростить наши вычисления, тем самым сохранив время?
Это метод рационализации (оптимизации, декомпозиции, замены множителей, замены функций, обобщенный метод интервалов, правило знаков)
Теоретическое обоснование метода
Часто, при решении логарифмических неравенств, встречаются задачи с переменным основанием логарифма. Так, неравенство вида

является стандартным школьным неравенством. Как правило, для его решения применяется переход к равносильной совокупности систем:


Недостатком данного метода является необходимость решения семи неравенств, не считая двух систем и одной совокупности. Уже при данных квадратичных функциях решение совокупности может потребовать много времени. Можно предложить альтернативный, менее трудоемкий метод решения этого стандартного неравенства. Это метод рационализации неравенств, известный в математической литературе под названием декомпозиции.
Метод декомпозиции
Метод декомпозиции заключается в замене сложного выражения F(x) на более простое выражение G(x), при которой неравенство G(x)^0 равносильно неравенству F(x)^0 в области определения F(x).
|
|
|
f, g, h – выражения с переменной х, a – фиксированное число или функция (а> 0, a≠ 1).
| Выражение F | Выражение G | |
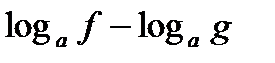
| 
| |

| 
| |
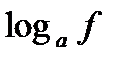
| 
| |
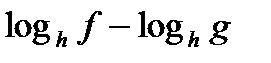
| 
| |
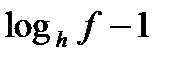
| 
| |
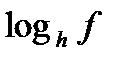
| 
| |
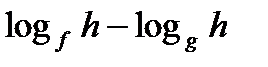
| 
| |

| 
| |
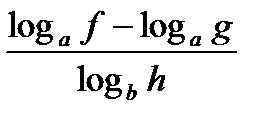
| 
| |
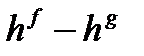
| 
| |

| 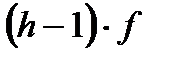
| |
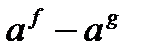
| 
| |

| 
| |

| 
| |
6 
| 
| 
|
Из данных выражений можно вывести некоторые следствия (с учетом области определения):


 0 ó
0 ó  0
0

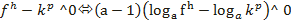
В указанных равносильных переходах символ ^ заменяет один из знаков неравенств: >, <, ≤, ≥.
Комментарий.
Стандартные ошибки, которые допускают учащиеся при использовании метода рационализации, заключаются в следующем:
а) проводят рационализацию без учета области определения данного неравенства;
б) применяют метод рационализации к неравенствам, не приведенным к стандартному виду F(x) ˅ 0;
в) формально применяют метод рационализации к выражениям вида
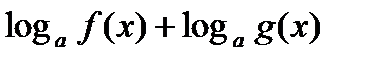 , заменяя на выражение
, заменяя на выражение 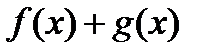 ;
;
г) подменяют формулировку «о совпадении знаков выражений для каждого
допустимого значения х» на неверную формулировку «о совпадении значений
выражений для каждого допустимого значения х».
Для решения:
1) Рассмотрим пример решения логарифмического неравенства двумя методами

1. Метод интервалов


| -11/6 |
| -5/3 |
| //////////////////////////// |
| x |

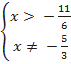
a) 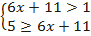 b)
b) 


| //////////////// |
| x |
| -5/3 |
| -11/6 |
| x |
| ////////////////// |
| x |
| /////// |
| x |
| ////////////////////// |
| Нет решений |
| -1 |
| x |
| x |
| -1 |
| -5/3 |
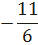
|

|
| ///////////////////// |

|

|
 ;
; 
Метод декомпозиции (рационализации)

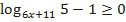



| ////////////////////////////////////////////////////////////////// |
| x |

|
| x |
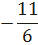
|
| ////////////////////////////////////////////////////////////////// |

|
| -1 |

|
Ответ: (; 
2) №17 из варианта 22 сборника Ященко И.В. 2015г.

1) 


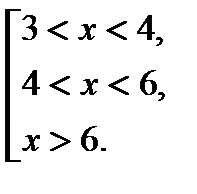
2)  ,
,
 ,
,
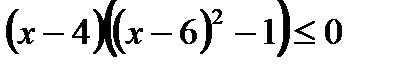 ,
,
 ,
,  ,
,
 ,
, 
 ,
,
 ,
,  ;
;
3) 
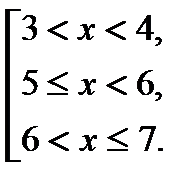
 U
U  U
U  .
.
Ответ.  ,
,  ,
,  .
.
3) №17 из варианта 23 сборника Ященко И.В. 2015г.

Решение.
1) 



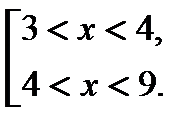
2)  ,
,
 ,
,
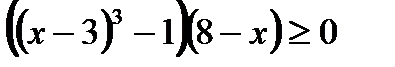 ,
,
 ,
, 
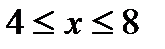 ;
;
3) 
 ,
, 
Ответ. 
4)№17 из варианта 18 сборника Ященко И.В. 2015г.
|
|
|

1) 
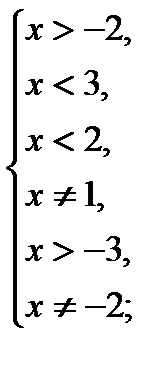
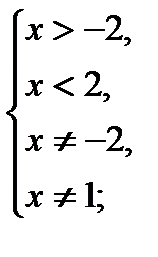

2)  ,
,
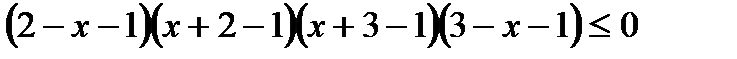 ,
,
 ,
,
 ,
,  ,
,  ,
,  ,
,
 ,
,  .
.
3) 

 U
U  .
.
Ответ.  ,
,  .
.
5) №17 из варианта 13 сборника Ященко И.В. 2015г
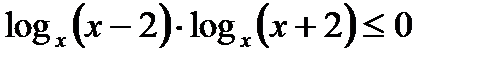 ,
,
1) 

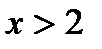 .
.
2) 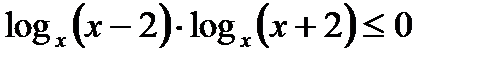 ,
,
 ,
,
 ,
,  ,
, 
 .
.
3) 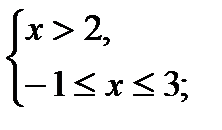
 .
.
Ответ. 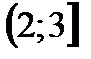 .
.
6) log12x2-41+35(3 – x) ≥ log2x2-5x+3(3- x).
Решение. Запишем неравенство в виде log12x2-41+35(3 – x) - log2x2-5x+3(3- x) ≥ 0 и заменим его равносильной системой, используя метод рационализации
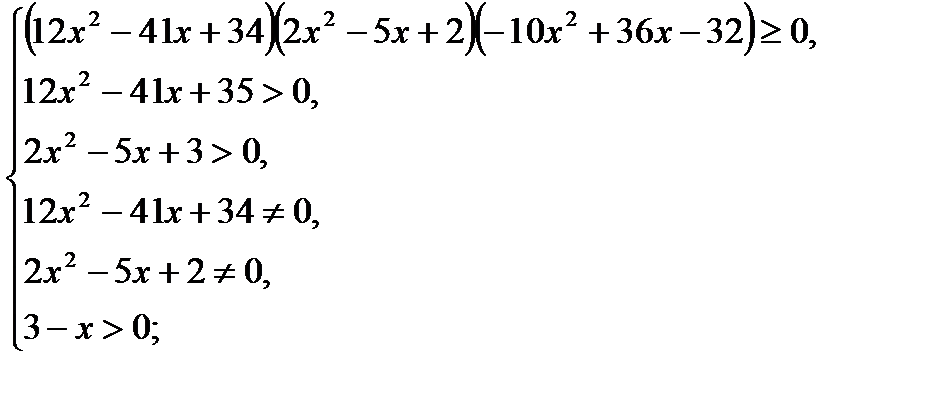

Для решения первых трёх неравенств системы используем метод интервалов.
Ответ: 
7)  ≥ 0.
≥ 0.
Решение. Заменим данное неравенство равносильной системой, используя метод рационализации




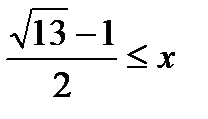 < 2.
< 2.
При решении неравенства (х – 1)(х – 2) < 0 системы учтены условия x < 3, x > 0, x ≠ 1. Условие 1 < x < 2 позволяет исключить множитель x – 1 > 0 в первом неравенстве системы.
Ответ:  .
.
Дополнительно 

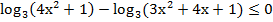
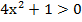



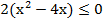
 [0; 4]
[0; 4]
| /////////////////////////////////////////////////////////////// |
| /////////////////////////////////////////////////////////////// |
| /////////////////////////////////////////////////////////////// |
| -1 |
| -1/3 |
| х |
| х |
Ответ: [0; 4]

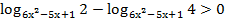
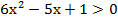
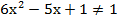

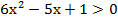 -2
-2 


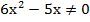

Ответ: 

Решение:

Ответ: (-1;1) U (3;5)
11) Решите неравенство log 2x+3 x2 < 1.
Решение. Запишем неравенство в виде log2x+3x2 – 1< 0 и заменим его равносильной системой, используя метод рационализации
(2x + 2)(x2 – 2x – 3) < 0
2x + 3 > 0
x ≠ 0
(x + 1)(x + 1)(x – 3) < 0
x > 1,5
x ≠ 0
Ответ: (-1.5; -1)  (-1; 0)
(-1; 0)  (0; 3).
(0; 3). 
12) Решите неравенство log|x+2|(4 + 7x – 2x2) ≤ 2.
Решение. Запишем нераенство в виде log|x + 2|(4 + 7x – 2x2) – log|x + 2|(x + 2)2 ≤ 0 и заменим равносильной системой, используя метод рационализации
(|x + 2| - 1)(4 + 7x – 2x2 – x2 – 4x – 4) ≤ 0
4 +7x - 2x2 > 0
x + 2 ≠ 0
((x + 2)2 – 1)(-3x2 + 3x) ≤ 0
(x + 0,5)(x – 4) < 0
x ≠ 2
x(x + 1)(x + 3)(x – 1) ≥ 0
(x + 0,5)(x – 4) < 0
x ≠ 2
Ответ: (-0,5; 0]  [1; 4).
[1; 4).
13)  .
.
Решение. Получим следующую систему неравенств:

Решая первые четыре неравенства, практически находим ОДЗ исходного неравенства:

Откуда:  .
.
Решим теперь пятое неравенство системы. После элементарных преобразований получим неравенство
 .
.
Умножим второй сомножитель на -1 и поменяем знак неравенства:
 .
.
Нетрудно заметить, что корнями второго множителя в этом неравенстве являются числа 1 и -2. Поэтому, раскладывая второй множитель на одночлены первого порядка, получаем:
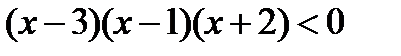 .
.
Это неравенство легко решить методом интервалов:  .
.
С учетом найденного ранее ОДЗ, получаем окончательный ответ.
Ответ:  .
.
|
|
|
14)) №17 из варианта 26 сборника Ященко И.В. 2015г.
1 способ (метод рационализации)

Решение.
1) 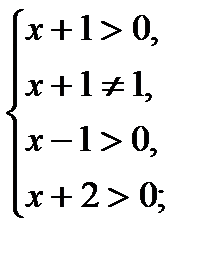
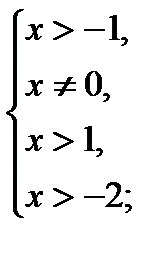
 .
.
2)  ,
,
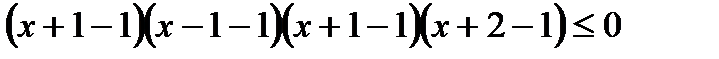 ,
,
 ,
,
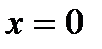 ,
,  ,
, 
 .
.
3) 

 .
.
Ответ.  .
.
2 способ
 ,
,
1) Область определения 
2) Логарифмическая функция с основанием большем 2 является возрастающей, тогда
а) 

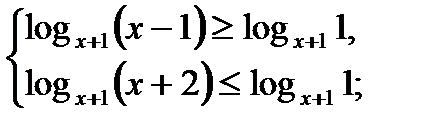

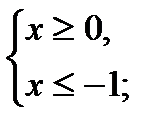 нет решений
нет решений
б) 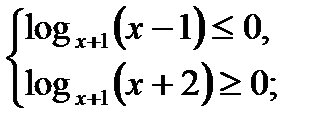


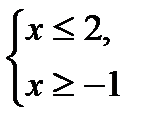
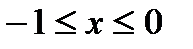 .
.
3) 

15) №17 из варианта 4 сборника Ященко И.В. 2015г.


Решение.
1) 


2)  ,
,
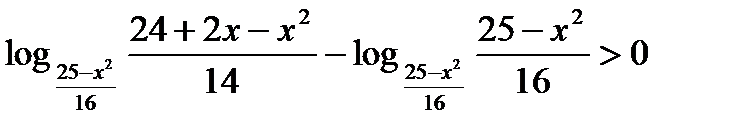 ,
,
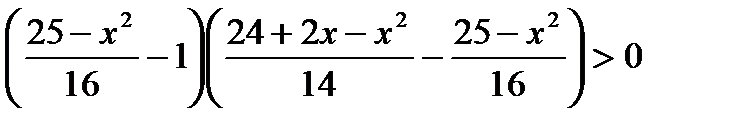 ,
,
 ,
,
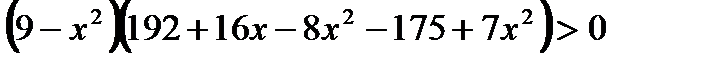 ,
,
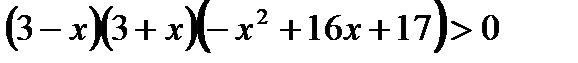 ,
,
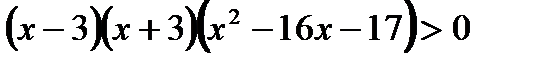 ,
,
 ,
,
 ,
, 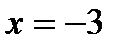 ,
,  ,
, 
 ,
, 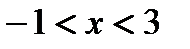 ,
,  .
.
3) 
 ,
, 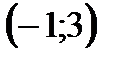 .
.
Ответ.  ,
,  .
.
16) №17 из варианта 27 сборника Ященко И.В. 2015г.

1) 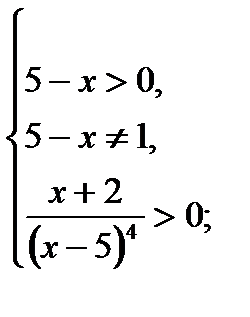
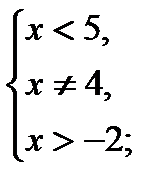

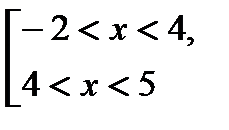
2)  ,
,
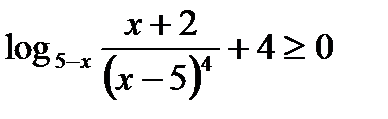 ,
,
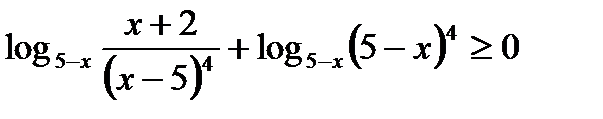 ,
,
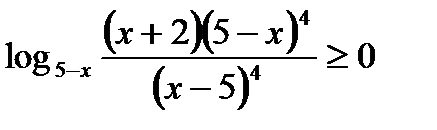 ,
,
 ,
,
 ,
,
 ,
,
 ,
, 
 .
.
3) 
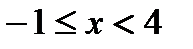
 .
.
Ответ.  .
.
17) 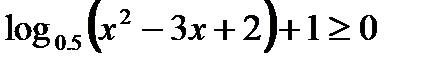
1) 
 ,
, 
 ,
, 
2) 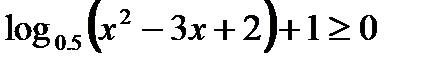 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
3) 
 ,
,  .
.
Ответ.  .
.
18)  .
.
1) 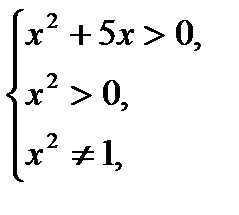


2)  ,
, 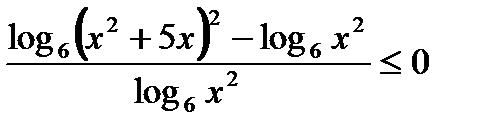 ,
,
 ,
,  ,
, 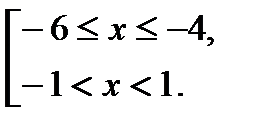
3) 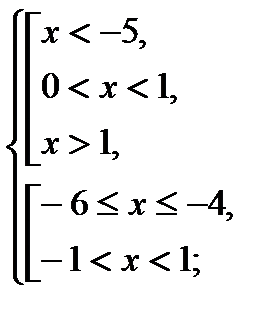
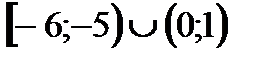 .
.
Ответ.  .
.
Дополнительно для самостоятельного решения:
1)  . Ответ.
. Ответ. 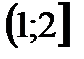 .
.
2) 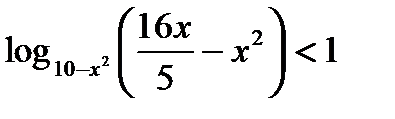 . Ответ.
. Ответ.  ,
,  .
.
3)  . Ответ.
. Ответ. 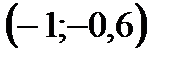
4)  . Ответ.
. Ответ.  .
.
5)  . Ответ.
. Ответ.  .
.
6)  . Ответ.
. Ответ. 
 .
.
7)  . Ответ.
. Ответ. 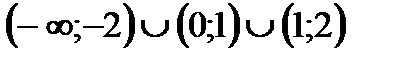 .
.
8)  . Ответ.
. Ответ.  .
.
9) 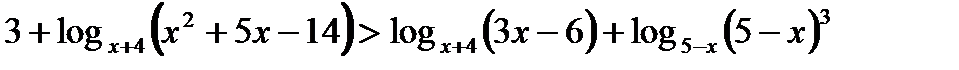 . Ответ.
. Ответ.  .
.
10)  .
.
Ответ.  .
.
Для работы с учениками:
Детям нужно рекомендовать использование метода рационализации в логарифмических неравенствах, когда неизвестное находится в основании степени.
Для отработки навыка решения предлагать решение в 3действия:
1. Найти область определения неравенства.
2. Использование замены функций по формулам рационализации.
3. Решить систему всех полученных условий.
Список литературы:
- Семенов А.Л., Ященко И.В. Математика 2015. 50 вариантов. М.: Экзамен, 2015
- Корянов А.Г., Прокофьев А.А. Математике ЕГЭ 2014. Типовые задания С3. Методы решения неравенств с одной переменной. www.alexlarin.net
- Лысенко Ф.Ф., Кулабухова С.Ю. Математика. Подготовка к ЕГЭ – 2014. Решаем задание С3 методом рационализации. Ростов-на-Дону: Легион, 2013
- Дмитрий Гущин. Математика. ЕГЭ – 2013: экспресс-курс для подготовки к экзамену. М.: Комсомольская правда, 2013
|
|
|


