 |
Необходимые и достаточные условия существования обратного оператора.
|
|
|
|
Лекция 5. ОБРАТНЫЙ ОПЕРАТОР И ОБРАТНАЯ МАТРИЦА
5.1. Определение. Взаимосвязь существования левого и правого обратных операторов в конечномерном пространстве.
5.2. Необходимые и достаточные условия существования обратного оператора.
5.3. Обратная матрица.
5.4. Теорема об обратном операторе произведения операторов, произведения оператора на число. Теорема об обратимости оператора, переводящего базис в базис.
5.5. Преобразование матрицы оператора при переходе к новому базису.
5.6. Преобразование координат вектора при изменении базиса.
5.1. Определение. Взаимосвязь существования левого и правого обратных
операторов в конечномерном пространстве.
Пусть 
– линейное пространство и 
– линейный оператор в нем.
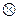Определение. Линейный оператор 
называется левым обратным оператору , если он удовлетворяет равенству 
.
Линейный оператор 
называется правым обратным оператору , если 
.
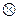Определение. Если существует оператор, являющийся одновременно и левым, и правым обратным к , то он называется обратным для оператора и обозначается 
. Т. е., определение обратного оператора:
.
При этом оператор называется обратимым (невырожденным).
Теорема. Почти очевидное утверждение: если оператор имеет одновременно и левый обратный и правый обратный , то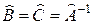 
.
Надо доказать: 
.
Доказательство:
.
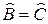Можно привести примеры, когда один односторонний обратный оператор существует, а второго нет. Действительно, рассмотрим бесконечномерное линейное пространство всех многочленов – 
и оператор дифференцирования, оператор интегрирования в нем:
, 
.
,
.
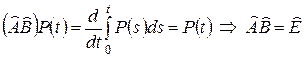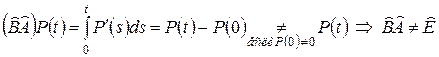Это в бесконечномерном пространстве, а как обстоит дело в конечномерном?
Докажем теорему: если – 
-мерное линейное пространство и – линейный оператор, действующий в нем, имеет левый обратный , то он является и правым обратным, т. е. является просто обратным оператором :
|
|
|
.
Доказательство:
Дано , – -мерное, в нем существует базис из векторов 
, 
, …, 
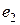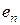. Рассмотри действие оператора на базисные векторы, результат обозначим 
: 
(
). (5.1)
Покажем, что векторы также образуют базис в .
Рассмотрим
.
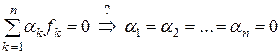Подставим в эту линейную комбинацию выражение вектора (5.1) и подействуем на нее оператором :
,
Поскольку векторы 
() – базисные. Следовательно, векторы тоже базисные. Подействуем на них оператором :
.
На полученный результат подействуем оператором :
.
Если линейный оператор не меняет базисных векторов, то он не меняет и любой вектор, являющийся линейной комбинацией базисных векторов:
.
Необходимые и достаточные условия существования обратного оператора.
Пусть – линейное пространство и – линейный оператор в нем.
Докажем утверждение: если линейный оператор переводит любой ненулевой вектор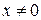 
в нулевой (обнуляет ненулевой вектор) 
, для него не существует обратного (никакого).
Доказательство:
Возьмем любой оператор , умножим его слева на и подействуем полученным оператором на любой вектор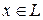 
:
.
Здесь использовано очевидное утверждение: любой линейный оператор переводит нулевой вектор в нулевой: 
.
С другой стороны, 
. Т.е. не существует.
Если в доказанном утверждении заменить любой ненулевой вектор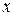 
на хотя-бы один такой, то доказывается отсутствие лишь левого обратного для .
Пример: рассмотрим -мерное арифметическое пространство и действующий в нем оператор , обращающий 1-ю координату в 0, а остольные не меняющий. Возьмем ненулевой вектор 
. Если , то у нет обратного.
Следовательно, необходимым условием существования обратного оператора является требование: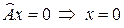 
, но достаточным оно не является.
|
|
|
Пример: пусть 
. Возьмем в нем оператор интегрирования : . Тогда необходимое условие имеет вид:
.
Здесь необходимое условие выполнено, а обратного оператора, как было показано ранее, вообще говоря, нет.
Теорема: В конечномерном пространстве необходимое условие существования обратного оператора 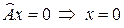является и достаточным.
Доказательство:
– -мерное линейное пространство, , , 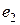…, 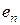– базис в нем. Подействуем оператором на базисные векторы, получим векторы 
(5.1). Покажем, что они также образуют базис.
.
,
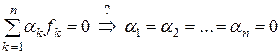поскольку векторы () – базисные. Следовательно, векторы тоже базисные.
Как было показано на предыдущей лекции, существует единственный линейный оператор , который переводит базисные векторы : 
.
Рассмотрим действие оператора 
на базисные векторы :
.
Если на базисных векторах оператор действует как единичный, то и для любого вектора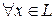 
имеем:
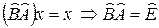
И так как – конечномерное пространство,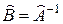 
.
Обратная матрица.
Пусть – -мерное линейное пространство и действующий в нем оператор обратим:
. (5.2)
Возьмем базис , , 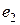…, 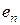. В этом базисе операторам и соответствуют некоторые матрицы. Обозначим их 
и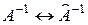 
. Естественно назвать 
матрицей, обратной матрице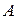 
.
Поскольку линейное пространство всех квадратных матриц -го порядка изоморфно всему пространству линейных операторов в другом соответствующем -мерном пространстве, то соответственно (5.2) получим:
. (5.3)
Если существует матрица , то матрица 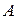называется обратимой (невырожденной). При взятии определителя от матричного равенства (5.3) получим числовое равенство:
.
Следовательно, если матрица 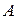обратима, то ее определитель не равен нулю. Если вспомнить явное выражение обратной матрицы через определитель исходной матрицы и алгебраические дополнения ее элементов, то можно сказать, что это необходимое условие обратимости матрицы является и достаточным.
5.4. Теорема об обратном операторе произведения операторов, произведения
оператора на число. Теорема об обратимости оператора, переводящего базис в базис.
Теорема: Если и – два обратимых оператора, то их произведение – также обратимый оператор, причем
;
Если – обратимый оператор и число 
, то оператор 
тоже обратимый, причем
.
Доказательство: Дано: 
: 
, 
.
|
|
|
Возьмем произведение операторов 
, умножим его слева на , а затем слева на 
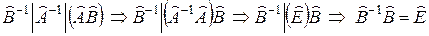, т.е. .
При умножении оператора 
на оператор 
опять получим единичный оператор 
, что доказывает сформулированное утверждение.
Теорема: Если оператор переводит базис в базис, то он обратимый оператор.
Доказательство: Дано: в -мерном линейном пространстве есть два базиса и (), причем 
;
. (5.4)
Преобразуем левую и правую стороны последнего соотношения (5.4): слева вместо подставим их выражения через и вынесем наружу оператор :
.
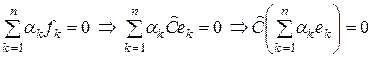Справа из нулевых коэффициентов сформируем нулевую линейную комбинацию векторов : 
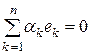. При этом соотношение (5.4) принимает вид:
, т.е. 
и с учетом конечномерности пространства оператор обратим.
|
|
|
