 |
Вывод дифференциальных уравнений осесимметрических движений круглой цилиндрической оболочки (безмоментная теория)
|
|
|
|
Введение
В последние годы быстрыми темпами развивается биомеханика - новая область естествознания, опирающаяся на механику сплошных сред и медицину. Внимание этой области направлено на теоретическое и практическое развитие медицинской практики с путем математического моделирования в рамках механики твердых, жидких и газообразных сред.
В курсовой работе будет рассматривается осесимметричное движения вязкой несжимаемой жидкости в круглой трубке, стенка которой представляет собой вязкоупругую ортотропную мембрану, прикрепленную к жесткой внешней структуре линейными связями.
В 1-й главе дадим выводдифференциальных уравнений осесимметричных движений круглой цилиндрической оболочки с учетом безмоментной теории. Далее будет рассмотрена постановка рассматриваемой задачи. Во 2-й главе преобразуются уравнения и граничные условии задачи,с учетом,что все переменные пропорциональны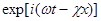 
, где 
- волновой шаг.
В 3-й главе работы получим дисперсионное уравнение для нахождения волнового числа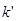 
.
Глава 1. Постановка задачи
Вывод дифференциальных уравнений осесимметрических движений круглой цилиндрической оболочки (безмоментная теория)
Пусть в невозмущённом состоянии оболочка представляет собой круглый тонкостенный цилиндр постоянного сечения, стенка которого имеет радиус a, плотность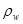 
, толщину h (см. рис.1). На стенки этой оболочки действует трансмуральное давление 
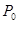. Обозначим T-окружное натяжение на единицу длины, соответствующее трансмуральному давлению т.е.
.
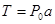На передний торец на единицу длины окружности действует продольное натяжение S.
Будем пользоваться полярной системой координат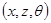 
и ограничимся рассмотрением осесиметричных возмущений, при которых перемещения в направлении 
отсутствуют.
|
|
|
Оболочка находится в предварительно натянутом состоянии, т.к. имеются напряжения закрепления, действующие со стороны окружающих сосуд тканей. Напряжения на стенке моделируются в предположении, что внешние ткани вносят дополнительную инерционность, жесткость и вязкоупругое демпфирование. Обозначим X и Y -напряжения закрепления в осевом и радиальном направлениях соответственно.
Из рассматриваемой оболочки вырежем малый элемент и составим уравнение равновесия этого элемента. Все внутренние и внешние усилия являются приведенными к срединной поверхности, причем она оказывается загруженной как распределенными усилиями, так и моментами. Однако, в случае тонких оболочек, моменты будут малы по сравнению с усилиями. Это позволяет считать, что действие внешних усилий будет определяться только действием распределенных сил (случай безмоментной теории). Такой подход позволяет рассматривать вместо равновесия элемента как единого целого, равновесие срединной поверхности (см. рис. 2).
Точки A,B, C, D срединной поверхности имеют только радиальное перемещение 
, следовательно, длины дуг AB и CD 
равны
,
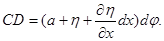
Площадь четырехугольника ABCD будет равна
.
Запишем уравнение изменения количества движения элемента оболочки в осевом направлении под действием указанных на рисунке сил.
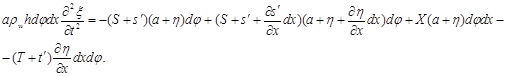
Это соотношение можно преобразовать к виду
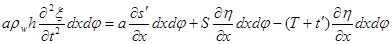
или
В этом уравнении учтены составляющие поперечных сил натяжения в осевом направлении (рис.3), которые появляются в результате деформации элемента оболочки.
Из рисунка 3 видно, что 
Аналогично записывается уравнение движения стенки в радиальном направлении. А именно
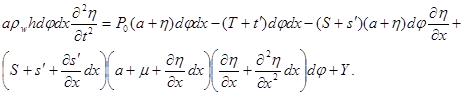
В этой формуле учтены составляющие продольных сил натяжения в радиальном направлении (Рис.4) которые появляются в результате деформации элемента оболочки.
|
|
|
Указанные на рисунке 4 приращения углов 
, равны:
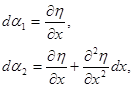
Окончательно, получаем
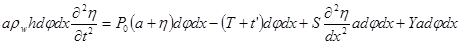или,
с учётом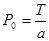 
уравнение движения стенки сосуда в радиальном направлении примет вид
.
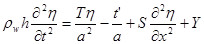Таким образом, уравнения движения стенки имеют
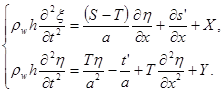(1.1)
|
|
|
