Уравнения Клапейрона и Клапейрона – Клаузиуса

Для однокомпонентных равновесных двухфазных систем зависимость между давлением, температурой, объемом и теплотой фазового перехода или полиморфного превращения (∆H_{ф. п.}) можно определить аналитически.

Как известно, если в ходе процесса изменение числа молей компонента i в какой-либо фазе (при постоянстве давления, температуры и числа молей остальных компонентов) равно единице (∆N _i =1), то изменение энергии Гиббса этой фазы равно химическому потенциалу i -гокомпонента µ_i
(∆G = µ_i).

Для однокомпонентной системы при p, T = const термодинамическим условием равновесия фаз является равенство химических по­тенциалов вещества во всех трех фазах:

µ^I =µ^II =µ^III или dG^I = dG^II = dG^III ,

а поскольку в отсутствии химических превращений в системе

dG =−SdT +Vdp, то−S ^IdT + V ^Idp =−S ^II dT + V ^II dp,

или

∆S_ф.п. dT =∆V_ф.п.dp,

где

∆S_{ф. п.} = S ^II − S^I , а ∆V_ф.п. = V ^II −V^I

Изменение энтропии объема при фазовых переходах или полиморфных превращениях. Тогда

 

Изотермические фазовые переходы и полиморфные превращения можно считать обратимыми процессами, поэтому, в соответствии со вторым началом термодинамики,

∆S_{ф. п.} =^∆Q ,

Где ∆Q – теплота процесса. А так как в изобарных условиях ∆Q_р=∆H, то

^dp=^{∆Hф. п.} . (3.6) dT T∆V_ф.п.

Это уравнение, применимое к любому двухфазному равновесному превращению, называется уравнениемКлапейрона.

При равновесии двух конденсированных фаз - твердое↔жидкое или твердое (модификация I) ↔ твердое (модификация II) – молярные объемы фаз сравнимы по величине. Так, молярный объем жидкой меди всего на 3% больше, чем твердой. Но при равновесиях твердое↔пар или жидкое↔пар в условиях, далеких от критических, молярный объем конденсированной фазы всегда значительно меньше, чем парообразной. Например, 10 молей воды при нормальных условиях в виде жидкости имеют объем 0,18 л, а в виде пара - 224 л, что почти в 1250 раз больше. Это позволяет преобразовать уравнение Клапейрона для процессов испарения и возгонки.

Для области давлений не более 5⋅10⁶ Па, в которой пар подчиняется законам идеальных газов, можно принять:

 

Вставить формулы

 

Это уравнение является частным случаем выражения (3.6) для процессов испарения и возгонки называется уравнением Клапейрона–Клаузиуса.

Интегрирование уравнения Клапейрона-Клаузиуса при условиях, когда ∆H_{ф. п.} можно считать независящей отт емпературы, приводит к выражению:

_∫d ln p = ^{∆Hисп.(возг.)} _∫^dT₂ +const,RT

ln p =− ^{∆Hисп.(возг.)} +const, (3.8)

RT

или, если обозначить ^{∆Hисп.(возг.)} =B, а^const =A, тоlg p =A −^B .

Согласно этим уравнениям, зависимость давления насыщенного пара от температуры в координатах lg p =f (1 T) является линейной (рис. 3.5).

^{1 11}рис. 3.5, 0

 

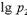
Если измерить давление насыщенного пара при различных температурах или температуру кипения (возгонки) при различных давлениях и построить прямую,как показано на рис. 3.5., то можно вычислить молярную теплоту испарения, т.е. количество теплоты, поглощенноевеществом при изотермическом испарении одного моля жидкости, находящейся в равновесии со своим паром. Аналогичным путем определяется и молярная теплота возгонки.

∆H_{исп.(возг.)}=2,3R ^lgp ₁¹⁻₋^lg₁ ^p2 =2,3R _T1 ^T1 ₋ ^T_T² ₂ lg _p^p1₂. (3.9)

В некоторых случаях пользуются не молярными теплотами испарения, возгонки, плавления ∆H, которые измеряются в кДж/моль, а удельными теплотами ∆h, которые относятся к 1 кг испаряемого вещества и измеряются в кДж/кг:

∆h =∆H ⋅1000/ M, (3.10)

где M – молярная масса вещества (г/моль).

Процессы испарения, возгонки и плавления являются эндотермическими (∆H>0); они идут с поглощением теплоты, которая расходуется на разрыв связей между молекулами жидкости при испарении или на разрушение кристаллической решетки при возгонке и плавлении.

При испарении и возгонке величина ∆V_{исп.(возг.)}>0 (а T_ф.п. всегда больше нуля), поэтому знак производной d ln p dT, как следует из уравнения (3.7), тоже положителен.

Из рис. 3.3 - 3.5 видно, что всегда при росте температуры (dT > 0) давление насыщенного пара над жидкостью и твердым веществом увеличивается (dp > 0). При этом, поскольку ∆H_возг. =∆H_пл. +∆H_исп.,
∆H_возг. >∆H_пл., криваяв озгонки AB идет круче кривой испарения AK (рис. 3.3 и 3.4). Следовательно, давление насыщенного пара с увеличением температуры растет сильнее над твердой фазой, чем над жидкой.

При плавлении изменение объема ∆V_ф.п. может быть и больше, и меньше нуля. Как правило, молярный объем жидкой фазы больше, чем твердой
(V_ж. > V_тв.), и с ростом внешнего давления температура плавления увеличивается: dp dT > 0 (рис. 3.3 а). Но для некоторых веществ (H₂O, Bi, Ga и ряда сплавов) наблюдается обратная зависимость (V_ж. < V_тв. и
dp dT < 0). Поэтому кривые плавления AD (рис. 3.3 а и 3.3 b) имеют различный уклон.

Во всех случаях, в соответствии с принципом Ле–Шателье, увеличение давления при постоянной температуре смещает фазовое равновесие в сторону того из процессов, который сопровождается уменьшением объема V (увеличением плотности ρ) системы. Например, из рис. 3.3 следует, что для серы при постоянной температуре V_ж > V_м > V_ри ρ _ж < ρ _м < ρ _р.

Поделиться:

Воспользуйтесь поиском по сайту: