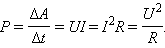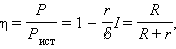|
Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.
|
|
|
|
ЭДС индукции
Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называется электромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением
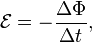
где  — поток магнитного поля через замкнутую поверхность
— поток магнитного поля через замкнутую поверхность  , ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).
, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).
Закон Ома
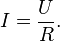
Закон открыт в 1826 году Георгом Омом и назван в его честь.
Ом записал свой закон (для полной цепи) в виде[1]:
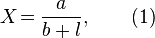
где:
- X — показания гальванометра; в современных обозначениях — сила тока I;
- a — величина, характеризующая свойства источника напряжения, постоянная (константа) в широких пределах и не зависящая от величины тока; в современных обозначениях — электродвижущая сила (ЭДС)
 ;
; - l — величина, определяемая длиной соединяющих проводов; в современных обозначениях — сопротивление внешней цепи R;
- b — параметр, характеризующий свойства всей электрической установки; в современных обозначениях — внутреннее сопротивление источника r.
В современных обозначениях закон Ома (1) имеет вид:
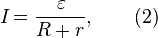
где:
-
 — ЭДС источника напряжения, В;
— ЭДС источника напряжения, В; -
 — сила тока, протекающего в цепи, А;
— сила тока, протекающего в цепи, А; -
 — сопротивление всех внешних элементов цепи, Ом;
— сопротивление всех внешних элементов цепи, Ом; -
 — внутреннее сопротивление источника напряжения, Ом.
— внутреннее сопротивление источника напряжения, Ом.
Из закона Ома для полной цепи вытекают два следствия:
- при r << R:
- сила тока в цепи обратно пропорциональна сопротивлению нагрузки (элементов цепи);
- в ряде случаев источник может быть назван источником напряжения;
- при r >> R:
- сила тока не зависит от свойств внешней цепи (от величины нагрузки);
- источник может быть назван источником тока.
Часто в школьных учебниках и научно-популярной литературе «законом Ома» называют выражение
|
|
|
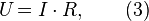
где 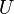 есть напряжение, падение напряжения или разность потенциалов между началом и концом участка проводника.
есть напряжение, падение напряжения или разность потенциалов между началом и концом участка проводника.
Выразив ЭДС из (2) и подставив (3), получим:
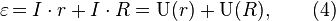
где:
-
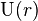 — падение напряжения на внутреннем сопротивлении источника;
— падение напряжения на внутреннем сопротивлении источника; -
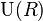 — падение напряжения на нагрузке (на внешней цепи).
— падение напряжения на нагрузке (на внешней цепи).
Сумма падений напряжения на внутреннем сопротивлении источника 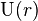 и на нагрузке (внешней цепи)
и на нагрузке (внешней цепи) 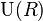 равна ЭДС источника.
равна ЭДС источника.
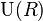 называют «напряжением на зажимах», поскольку именно его значение показывает вольтметр, подключённый к началу и концу замкнутой цепи.
называют «напряжением на зажимах», поскольку именно его значение показывает вольтметр, подключённый к началу и концу замкнутой цепи. 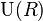 всегда меньше ЭДС.
всегда меньше ЭДС.
К формуле (3), записанной в виде
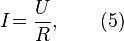
применима другая формулировка:

| Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи. | 
|
Выражение (5) можно переписать в виде:
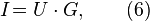
где коэффициент пропорциональности 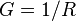 назван проводимость или электропроводность. Изначально единицей измерения проводимости был Ом-1 или 1/Ом — «Mо»[2], в международной системе единиц (СИ) единицей измерения проводимости является си́менс
назван проводимость или электропроводность. Изначально единицей измерения проводимости был Ом-1 или 1/Ом — «Mо»[2], в международной системе единиц (СИ) единицей измерения проводимости является си́менс
Правила Кирхгофа.
Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют любой двухполюсник, входящий в цепь, например, на рис. отрезок, обозначенный R1, I1 есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый цикл из ветвей. Термин замкнутый цикл означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.
|
|
|
В терминах данных определений правила Кирхгофа формулируются следующим образом.
Первое правило
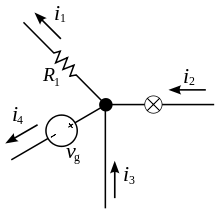
Сколько тока втекает в узел, столько из него и вытекает. i 2 + i 3 = i 1 + i 4
Первое правило Кирхгофа гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу равна сумме направленных от узла.
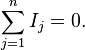
Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.
Второе правило
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
для постоянных напряжений 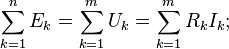
для переменных напряжений 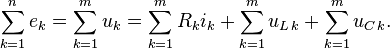
Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.
Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).
Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.
Работа и мощность тока
При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = I Δt. Электрическое поле на выделенном учестке совершает работу
| ΔA = (φ1 – φ2) Δq = Δφ12 I Δt = U I Δt, |
где U = Δφ12 – напряжение. Эту работу называют работой электрического тока.
|
|
|
Если обе части формулы
| RI = U, |
выражающей закон Ома для однородного участка цепи с сопротивлением R, умножить на IΔt, то получится соотношение
| R I2 Δt = U I Δt = ΔA. |
Это соотношение выражает закон сохранения энергии для однородного участка цепи.
Работа Δ A электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло Δ Q, выделяющееся на проводнике.
|
Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем и носит название закона Джоуля–Ленца.
Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена:
|
Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт).
Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой 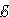 и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. Закон Ома для полной цепи записывается в виде
и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. Закон Ома для полной цепи записывается в виде
(R + r) I = 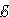 . .
|
Умножив обе части этой формулы на Δq = IΔt, мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока:
R I2Δt + r I2Δt = 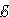 IΔt = ΔAст. IΔt = ΔAст.
|
Первый член в левой части ΔQ = R I2Δt – тепло, выделяющееся на внешнем участке цепи за время Δt, второй член ΔQист = r I2Δt – тепло, выделяющееся внутри источника за то же время.
Выражение 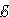 IΔt равно работе сторонних сил ΔAст, действующих внутри источника.
IΔt равно работе сторонних сил ΔAст, действующих внутри источника.
При протекании электрического тока по замкнутой цепи работа сторонних сил Δ A ст преобразуется в тепло, выделяющееся во внешней цепи (Δ Q) и внутри источника (Δ Q ист).
. |
Следует обратить внимание, что в это соотношение не входит работа электрического поля. При протекании тока по замкнутой цепи электрическое поле работы не совершает; поэтому тепло производится одними только сторонними силами, действующими внутри источника. Роль электрического поля сводится к перераспределению тепла между различными участками цепи.
|
|
|
Внешняя цепь может представлять собой не только проводник с сопротивлением R, но и какое-либо устройство, потребляющее мощность, например, электродвигатель постоянного тока. В этом случае под R нужно понимать эквивалентное сопротивление нагрузки. Энергия, выделяемая во внешней цепи, может частично или полностью преобразовываться не только в тепло, но и в другие виды энергии, например, в механическую работу, совершаемую электродвигателем. Поэтому вопрос об использовании энергии источника тока имеет большое практическое значение.
Полная мощность источника, то есть работа, совершаемая сторонними силами за единицу времени, равна
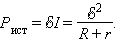
|
Во внешней цепи выделяется мощность
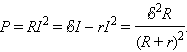
|
Отношение 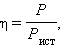 равное
равное
|
называется коэффициентом полезного действия источника.
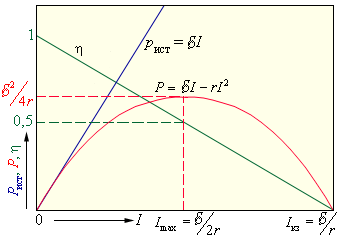
На рис. 1.11.1 графически представлены зависимости мощности источника Pист, полезной мощности P, выделяемой во внешней цепи, и коэффициента полезного действия η от тока в цепи I для источника с ЭДС, равной 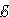 , и внутренним сопротивлением r. Ток в цепи может изменяться в пределах от I = 0 (при
, и внутренним сопротивлением r. Ток в цепи может изменяться в пределах от I = 0 (при 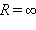 ) до
) до  (при R = 0).
(при R = 0).
|
| Рисунок 1.11.1. Зависимость мощности источника Pист, мощности во внешней цепи P и КПД источника η от силы тока |
Из приведенных графиков видно, что максимальная мощность во внешней цепи Pmax, равная
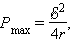
|
достигается при R = r. При этом ток в цепи
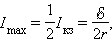
|
а КПД источника равен 50 %. Максимальное значение КПД источника достигается при I → 0, т. е. при R → ∞. В случае короткого замыкания полезная мощность P = 0 и вся мощность выделяется внутри источника, что может привести к его перегреву и разрушению. КПД источника при этом обращается в нуль.
Закон Джоуля-Ленца
В словесной формулировке звучит следующим образом[2]
Мощность тепла, выделяемого в единице объёма среды при протекании электрического тока, пропорциональна произведению плотности электрического тока на величину напряженности электрического поля
Математически может быть выражен в следующей форме:
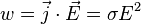
где 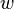 — мощность выделения тепла в единице объёма,
— мощность выделения тепла в единице объёма, 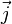 — плотность электрического тока,
— плотность электрического тока, 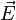 — напряжённость электрического поля, σ — проводимость среды, а точкой обозначено скалярное произведение.
— напряжённость электрического поля, σ — проводимость среды, а точкой обозначено скалярное произведение.
Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивления участка
В интегральной форме этот закон имеет вид

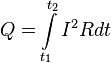
где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t1 до t2.
|
|
|
В случае постоянных силы тока и сопротивления:
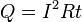
|
|
|