 |
V1: гармонические колебания
|
|
|
|
I:
S: Гармоническими называются колебания:
-: которые возникают в системе при участии внешней силы
-: при которых их амплитуда под действием силы трения постепенно уменьшается
+: при которых колеблющаяся величина изменяется в зависимости от времени по закону синуса или косинуса
-: при которых механические возмущения распространяются в пространстве и переносят энергию
-: при которых их скорость остается постоянной
I:
S: Примером гармонических колебаний могут служить:
+: колебания математического маятника
-: колебания физического маятника
-: периодические подскакивания в реальных условиях мяча, упавшего на землю
-: круги, расходящиеся на поверхности воды от брошенного камня
-: колебания температуры окружающей среды
I:
S: Фаза колебаний представляет собой:
-: величину, численно равную времени, в течение которого совершается одно полное колебание
-: величину, численно равную наибольшему отклонению колеблющегося тела от положения равновесия
-: величину, численно равную числу колебаний за единицу времени
+: величину, характеризующую положение колеблющейся точки в данный момент времени
-: величину скорости распространения колебаний в данный момент времени
I:
S:Уравнение гармонических колебаний было получено в предположении:
+: малости отклонения маятника от положения равновесия
-: наличия вынуждающей силы, действующей на маятник
-: отсутствия начальной фазы колебания
: равенства нулю кинетической энергии маятника в положении равновесия
-: наличия силы трения в точке подвеса маятника
S:В выражении для смещения материальной точки X = А0sin(ω0t +...) в случае гармонических колебаний пропущен символ:
+: 
|
|
|
-: 
-: 
-: 
-: 
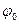
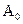
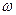
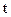
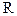
I:
S: Гармонические колебания описываются уравнением:
+: 
-: 
-: 
-: 
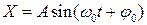
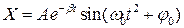
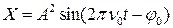
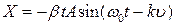
I:
S: Не могут служить примером гармонических колебаний:
-: колебания математического маятника
+: затухающие колебания
-: электромагнитные колебания в колебательном контуре
-: колебания физического маятника
-: колебания груза на пружине
I:
S: Неверным является утверждение о том, что:
-: амплитуда гармонических колебаний не зависит от их частоты
-: амплитуда гармонических колебаний не зависит от их периода
+: частота колебаний не зависит от их периода
-: смещение колеблющейся точки зависит от фазы колебаний
-: смещение колеблющейся точки зависит от времени
I:
S: Неверным является утверждение о том, что гармонические колебания:
+: совершаются по экспоненциальному закону
-: совершаются по закону косинуса
-: могут иллюстрироваться периодическими изменениями температуры
-: это явления, при которых система, будучи выведена из состояния равновесия, возвращается в него через равные промежутки времени
-: совершаются при условии отсутствия затухания
I:
S: При увеличении длины математического маятника вдвое его частота:
-: Уменьшится в 2 раза
-: Увеличится в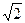 
раз
-: Увеличится в 2 раза
+: Уменьшится в 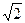раз
-: Не изменится
I:
S: При уменьшении массы пружинного маятника вдвое его период колебаний:
-: Уменьшится в 2 раза
-: Увеличится в 2 раза
-: Увеличится в 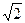раз
+: Уменьшится в 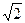раз
-: Не изменится
I:
S: При перенесении математического маятника на Луну:
-: Амплитуда его колебаний увеличится
-: Амплитуда его колебаний уменьшится
+: Период его колебаний увеличится
-: Период его колебаний уменьшится
-: Частота его колебаний не изменится
I:
S: При перенесении пружинного маятника в условия невесомости:
-: Частота его колебаний увеличится
-: Период его колебаний увеличится
+: Период его колебаний не изменится
-: Маятник колебаться не будет
|
|
|
-: Частота его колебаний уменьшится
I:
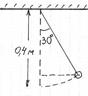
S: На рисунке изображен математический маятник. Амплитуда колебаний маятника равна:
-: 10 см
+: 20 см
-: 30 см
-: 40 см
-: 0,5 м
I:
S: Период колебаний данного маятника равен:
-: 
+: 
-: 
-: 
-: 
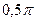
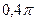
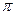
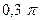
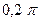
I:
S: Согласно графику, смещение колеблющейся точки через 4 с после начала движения составляет:
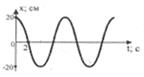
-: 5 см
-: 10 см
+: 20 см
-: 30 см
-: 40 см
I:
S: На рисунке изображен математический маятник. Амплитуда колебаний маятника равна:
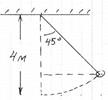
-: 4 м
+: 3 м
-: 2 м
-: 1 м
-: 0,5 м
I:
S: Частота колебаний данного маятника равна:
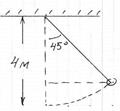
-: 2 с-1
-: 1 с-1
-: 0,5 с-1
-: 4 с-1
+: 0,25 с-1
I:
S: Волна с частотой 10 Гц распространяется в некоторой среде, причем разность фаз в двух точках, находящихся на расстоянии 1 м одна от другой на одной прямой с источником колебаний, равна π радиан. Скорость распространения волны в этой среде будет равна:
-: 5 м/с
-: 1 м/с
-: 10 м/с
+: 20 м/с
-: 100 м/с
V1: МЕХАНИЧЕСКИЕ ВОЛНЫ
I:
S: В выражении для смещения материальной точки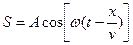 
в случае гармонических колебаний, символ S означает:
-: амплитуду колебаний
-: фазу волны
-: расстояние между соседними гребнями волн
-: произвольную координату
+: смещение точки, участвующей в волновом процессе
I:
S: В уравнении волны 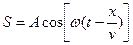символ x представляет собой:
-: смещение точки, участвующей в волновом процессе
+: произвольную координату
-: амплитуду колебаний
-: фазу волны
-: расстояние между соседними гребнями волн
I:
S: Длиной волны называется:
-: расстояние между двумя соседними точками на оси OY, колеблющимися в одинаковых фазах
+: расстояние между двумя соседними точками на оси OX, колеблющимися в одинаковых фазах
-: расстояние между двумя соседними точками на оси OX, колеблющимися в противоположных фазах
-: расстояние, пробегаемое волной за единицу времени
-: наибольшее отклонение точек волны от положения равновесия
I:
S: Вектором Умова называют:
+: величину, равную потоку энергии волн, проходящему через единичную площадь, перпендикулярную этому направлению
-: вектор, перпендикулярный направлению распространения волны
-: величину, равную плотности энергии волны
-: величину кинетической энергии, переносимой волной
-: величину, показывающую скорость затухания волны
|
|
|
I:
S: Вектор Умова определяется выражением:
-: 
+: 
-: 
-: 
-: 
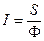
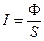
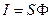
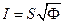
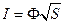
I:
S: В выражении для интенсивности волны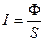 
величина Ф представляет собой:
-: длину волны
-: амплитуду волны
+: поток энергии волн
-: плотность энергии волн
-: энергию волн
I:
S: Механической волной называется:
-: механические колебания, описываемые по гармоническому закону
-: механическое возмущение, возникающее в твердом теле при его деформации
-: перенос энергии в упругой среде
+: механическое возмущение, распространяющееся в пространстве и несущее энергию
-: периодическое отклонение тела от положения равновесия
I:
S: Уравнение волны записывается в следующем виде:
+: 
-: 
-: 
-: 
-: 
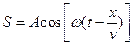
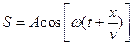
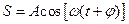
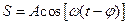
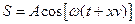
I:
S: Скорость распространения волны определяется выражением:
-: 
-: 
+: 
-: 
-: 
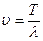
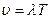
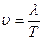
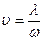
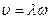
I:
S: За время 4/3 секунды волна распространилась на расстояния равное длине волны. Частота колебаний волны равна:
+: 0,75 Гц
-: 1 Гц
-: 10 Гц
-: 0,25 Гц
-: 250 Гц
I:
S: Скорость распространения звука в материале, в котором колебания с периодом 0,01 с вызывают звуковую волну, имеющую длину 10 м, составляет:
-: 100 м/с
+: 1000 м/с
-: 10 км/с
-: 10 м/с
-: 100 км/с
I:
S: Частота колебаний волны с длиной волны 3 м и скоростью распространения 12 м/с составляет:
-: 0,25 Гц
-: 25 Гц
-: 0,4 Гц
+: 4 Гц
-: 0,5 Гц
V1: СТАТОБРАБОТКА
I:
S: В соответствии с приведенной таблицей коэффициент Стьюдента для пяти измерений и доверительной вероятности 0,98 составляет
| n | p | |||||
| 0,7 | 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | |
| 2,0 | 3,1 | 6,3 | 12,7 | 31,8 | 63,7 | |
| 1,3 | 1,9 | 2,9 | 4,3 | 7,0 | 9,9 | |
| 1,3 | 1,6 | 2,4 | 3,2 | 4,5 | 5,8 | |
| 1,2 | 1,5 | 2,1 | 2,8 | 3,7 | 4,6 | |
| 1,2 | 1,5 | 2,0 | 2,6 | 3,4 | 4,0 | |
| 1,1 | 1,4 | 1,9 | 2,4 | 3,1 | 3,7 |
-: 1,2;
-: 2,8;
+: 3,7;
-: 1,9;
-: 2,3.
I:
S: Для шести измерений коэффициенту Стьюдента равному 2,6 соответствует доверительная вероятность
| n | p | |||||
| 0,7 | 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | |
| 2,0 | 3,1 | 6,3 | 12,7 | 31,8 | 63,7 | |
| 1,3 | 1,9 | 2,9 | 4,3 | 7,0 | 9,9 | |
| 1,3 | 1,6 | 2,4 | 3,2 | 4,5 | 5,8 | |
| 1,2 | 1,5 | 2,1 | 2,8 | 3,7 | 4,6 | |
| 1,2 | 1,5 | 2,0 | 2,6 | 3,4 | 4,0 | |
| 1,1 | 1,4 | 1,9 | 2,4 | 3,1 | 3,7 |
-: 0,7;
-: 0,8;
-: 0,85;
-: 0,9;
+: 0,95.
I:
S: При коэффициенте Стьюдента равном 2,6 доверительная вероятность 0,95 может быть обеспечена при количестве измерений равном
|
|
|
| n | p | |||||
| 0,7 | 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | |
| 2,0 | 3,1 | 6,3 | 12,7 | 31,8 | 63,7 | |
| 1,3 | 1,9 | 2,9 | 4,3 | 7,0 | 9,9 | |
| 1,3 | 1,6 | 2,4 | 3,2 | 4,5 | 5,8 | |
| 1,2 | 1,5 | 2,1 | 2,8 | 3,7 | 4,6 | |
| 1,2 | 1,5 | 2,0 | 2,6 | 3,4 | 4,0 | |
| 1,1 | 1,4 | 1,9 | 2,4 | 3,1 | 3,7 |
-: 3;
-: 4;
-: 5;
+: 6;
-: 8.
I:
S: При многократных измерениях некоторой физической величины были получены следующие значения: 45; 44; 44; 46; 44; 126; 45. При этом среднее значение измеряемой величины равно
+: 45;
-: 44;
-: 56;
-: 60;
-: 72.
I:
S: При многократных измерениях некоторой физической величины были получены следующие значения: 10; 12; 11; 10; 12. При этом абсолютная погрешность первого измерения составила
+: 1;
-: 2;
-: 3;
-: 4;
-: 5.
I:
S: При статистической обработке данных измерений некоторой физической величины было получено ее среднее значение равное 12, а средняя абсолютная погрешность измерений составила 3. При этом относительная погрешность измерений составила
-: 15%;
-: 9%;
-: 36%;
+: 25%;
-: 40%.
I:
S: При статистической обработке данных измерений некоторой физической величины было получено ее среднее значение равное 12, а случайная погрешность измерений составила 2. При этом доверительный интервал составляет
-: От 2 до 12;
-: От 10 до 12;
+: От 10 до 14;
-: От 2 до 14;
-: От 0 до 12.
I:
S: Окончательная запись результатов измерений записана неверно в выражении
-: 284±1;
-: 350±38;
-: 52,7±0,3;
+: 284,5±1;
-: 4,750±0,006.
I:
S: По данным пяти измерений были получены следующие значения измеряемой величины: 40; 30; 30; 30; 30. При этом средняя арифметическая погрешность измерений составила
-: 2;
+: 3;
-: 4;
-: 5;
-: 6.
I:
S: По данным пяти измерений были получены следующие значения измеряемой величины: 40; 30; 30; 30; 30. При этом средняя квадратичная погрешность измерений составила
-: 1;
-: 2;
-: 3;
+: 4;
-: 5.
I:
S: По данным пяти измерений были получены следующие значения измеряемой величины: 40; 30; 30; 30; 30. При этом случайная погрешность измерений составила
-: 1;
-: 2;
-: 3;
-: 4;
+: 5.
I:
S: По данным пяти измерений были получены следующие значения измеряемой величины: 70; 70; 60; 60; 70. При этом средняя арифметическая погрешность измерений составила
-: 2;
-: 3;
-: 4;
+: 5;
-: 6.
I:
S: По формуле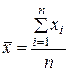 
рассчитывается
-: Средняя арифметическая погрешность;
+: Среднее арифметическое значение;
-: Средняя квадратичная погрешность измерения;
-: Абсолютная погрешность отдельного измерения;
-: Относительная погрешность.
I:
S: По формуле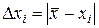 
рассчитывается
-: Средняя арифметическая погрешность;
-: Среднее арифметическое значение;
-: Средняя квадратичная погрешность измерения;
+: Абсолютная погрешность отдельного измерения
-: Относительная погрешность.
I:
|
|
|
S: По формуле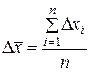 
рассчитывается
+: Средняя арифметическая погрешность;
-: Среднее арифметическое значение;
-: Средняя квадратичная погрешность измерения;
-: Абсолютная погрешность отдельного измерения
-: Относительная погрешность.
I:
S: По формуле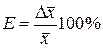 
рассчитывается
-: Средняя арифметическая погрешность;
-: Среднее арифметическое значение;
-: Средняя квадратичная погрешность измерения;
-: Абсолютная погрешность отдельного измерения
+: Относительная погрешность.
I:
S: По формуле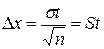 
рассчитывается
-: Средняя арифметическая погрешность;
-: Среднее арифметическое значение;
+: Случайная погрешность;
-: Абсолютная погрешность отдельного измерения
-: Относительная погрешность.
I:
S: По формуле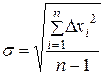 
рассчитывается
+: Средняя квадратичная погрешность измерения;
-: Среднее арифметическое значение;
-: Случайная погрешность;
-: Абсолютная погрешность отдельного измерения
-: Относительная погрешность.
V1: ЭФФЕКТ ДОПЛЕРА
I:
S: Эффект Доплера заключается в изменении:
-: скорости распространения волн, воспринимаемых наблюдателем, при относительном движения источника волн и наблюдателя
+: частоты волн, воспринимаемых наблюдателем, вследствие относительного движения источника волн и наблюдателя
-: громкости звука, воспринимаемого наблюдателем, вследствие относительного движения источника звука и приемника
-: интенсивности волн, воспринимаемых наблюдателем, вследствие относительного движения источника звука и приемника
-: фазы сигнала, воспринимаемого наблюдателем, вследствие относительного движения источника звука и приемника
I:
S: Эффект Доплера наблюдается:
-: только для ультразвука
-: только для света
-: только для звука
-: только для электромагнитных волн
+: для любых волн
I:
S: Эффект Доплера описывается выражением:
-: 
-: 
-: 
-: 
+: 
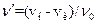
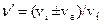
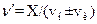
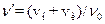
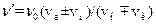
I:
S: В формуле для эффекта Доплера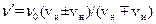 
символ ν0 означает:
-: длину волны сигнала, испускаемого источником
-: скорость распространения сигнала в среде
+: частоту сигнала, испускаемого источником
-: скорость движения источника сигнала
-: амплитуду колебаний звуковой волны
I:
S: В гемодинамике УЗ эффект Доплера применяется для:
-: определения диаметра кровеносных сосудов
+: определения скорости кровотока
-: изучения распределения фармпрепаратов в организме человека
-: определения скорости оседания эритроцитов
-: визуализации внутренних органов человека
I:
S: В кардиологии УЗ эффект Доплера позволяет определить:
-: нарушения режима работы СА-узла
-: характер помех, возникающих при записи электрокардиограмм
-: изменение сечения аорты
-: визуализации желудочков сердца
+: клапанные нарушения сердца
V1: ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
I:
S: Элементарными заряженными частицами являются
+: протоны
-: нейтроны
-: атомы
-: молекулы
-: изотопы
I:
S: Неподвижные электрические заряды взаимодействуют по закону
-: Ленца
-: Стокса
+: Кулона
-: Ома
-: Фарадея
I:
S: Сила взаимодействия неподвижных электрических зарядов определяется выражением
-: 
;
+: 
-: 
-: 
-: 
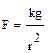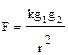
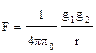
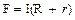
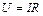
I:
S: Напряженность поля является его
-: Энергетической характеристикой
-: Емкостной характеристикой
-: Индукционной характеристикой
-: Динамической характеристикой
+: Силовой характеристикой
I:
S: Единицей измерения напряженности электрического поля является
-: Вольт
-: Ампер
-: Ампер/с
+: Вольт/м
-: Фарад
I:
S: Напряженность электрического поля, создаваемого точечным зарядом, описывается выражением
+: 
;
-:
-:
-:
-: 
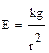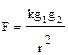
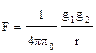
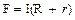
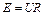
I:
S: Потенциал поля является его
+: Энергетической характеристикой
-: Емкостной характеристикой
-: Индукционной характеристикой
-: Динамической характеристикой
-: Силовой характеристикой
I:
S: Для расчета потенциала электрического поля, создаваемого точечным зарядом, следует воспользоваться выражением
-: 
;
-: 
+: 
-: 
-: 
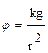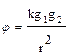
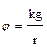
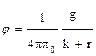
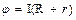
I:
S: Единицей измерения потенциала электрического поля является
+: Вольт
-: Ампер
-: Ампер/с
-: Вольт/м
-: Фарад
I:
S: Напряженность электрического поля и разность потенциалов связаны выражением
-: 
-: 
+: 
-: 
-: 
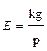
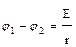
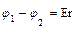
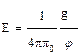
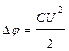
I:
S: Физический смысл диэлектрической проницаемости среды состоит в том, что она показывает
-: Плотность среды, в которой находится поле
-: Величину энергии электрического поля
-: Густоту линий индукции
+: Во сколько раз сила взаимодействия электрических зарядов в вакууме больше, чем в данной среде
-: Во сколько раз сила взаимодействия электрических зарядов в вакууме меньше, чем в данной среде
I:
S: Для потока напряженности электрического поля справедливо выражение
+: 
-: 
-: 
-: 
-:
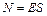
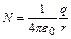
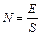
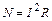
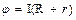
I:
S: В соответствии с теоремой Остроградского-Гаусса поток напряженности электрического поля, пронизывающий любую замкнутую поверхность, окружающую электрические заряды, пропорционален
-: Произведению заряда, находящегося внутри замкнутой поверхности, на напряженность поля
-: Произведению потенциала поля на площадь замкнутой поверхности
-: Силе, приходящейся на единицу площади замкнутой поверхности
-: Произведению напряженности поля на потенциал внутри замкнутой поверхности
+: Алгебраической сумме зарядов, находящихся внутри замкнутой поверхности
I:
S: Напряженность поля электрического диполя на продолжении оси диполя равна
-: 
+: 
-: 
-: 
-:
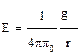
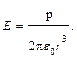
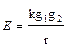
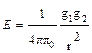
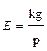
V1: КОНТАКТНЫЕ ЯВЛЕНИЯ
I:
S: Элементарными заряженными частицами являются
+: протоны
-: нейтроны
-: атомы
-: молекулы
-: изотопы
I:
S: Возникновение контактной разности потенциалов возможно при соприкосновении
-: Серебра с янтарем
+: Алюминия с серебром
-: Золота с алмазом
-: Ртути со стеклом
-: Стекла с алюминием
I:
S: Контактная разность потенциалов зависит от
-: Плотности контактирующих элементов
: Их масс
-: Их валентностей
+: Их химического состава
-: Их теплопроводностей
I:
S: Контактная разность потенциалов зависит от
-: Плотности контактирующих элементов
: Их масс
-: Их валентностей
-: Их теплопроводностей
+: Их температуры
I:
S: Цепь состоит из четырех разнородных металлов, соединенных последовательно. В цепи возникают следующие разности потенциалов: в первом контакте 4 В, во втором – 3 В, в третьем – 2 В, в четвертом – 1 В. При этом разность потенциалов на концах цепи составит
-: 1 В
+: 3 В
-: 5 В
-: 7 В
-: 9 В
I:
S: Замкнутая цепь состоит из трех последовательно соединенных разнородных металлов с работами выхода 1 эВ, 2 эВ и 3 эВ При этом на концах цепи возникает контактная разность потенциалов равная
+: 0 В
-: 3 В
-: 5 В
-: 7 В
-: 9 В
I:
S: Явление термоэлектричества состоит в
-: Увеличении сопротивления металлов при их нагревании
-: Явлении нагревания проводников при прохождении через них электрического тока
+: Зависимости контактной разности потенциалов от температуры
-: Явлении резкого повышения температуры контактирующих элементов при коротком замыкании
-: Зависимости сопротивления металлов от температуры
I:
S: Явление термоэлектричества возникает в
-: Полупроводниках с электронной проводимостью
-: Полупроводниках с дырочной проводимостью
-: Контактах диэлектрика с металлом
+: Разнородных металлах
-: Однородных металлах
I:
S: Явление термоэлектричества описывается выражением
-: Dj=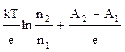 
-: Dj=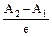 
+: E=α(t1-t2);
-: U=I2R
-: Dj=ER
I:
S: В выражении для термо-ЭДС E=α(t1-t2) символ α означает
-: Удельное сопротивление материала
-: Измеряемую температуру
-: Разность потенциалов между контактирующими элементами
-: Термоток
+: Чувствительность прибора
I:
S: Термоэлектричество лежит в основе работы
+: Термопары
-: Транзистора
-: Электронного осциллографа
-: Полупроводникового диода
-: Электрокардиографа
I:
S: По сравнению с жидкостными термометрами термопара имеет следующие преимущества
-: Компактность
+: Безинерционность
+: Точность
-: Дешевизна
-: Электробезопасность
V1: МАГНИТНОЕ ПОЛЕ
I:
S: Для определения величины напряженности магнитного поля проводника с током следует воспользоваться выражением
-: 
+: 
-: 
-: 
-: 
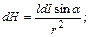
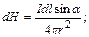
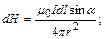
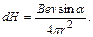
I:
S: Величина напряженности магнитного поля определяется как
+: Отношение силы, с которой поле действует на единичный элемент тока (расположенный
перпендикулярно полю в вакууме), к магнитной постоянной
-: Сила, с которой поле действует на единичный заряд, помещенный в данную толчку поля
-: Произведение индукции магнитного поля на величину тока в проводнике
-: Произведение элемента тока на магнитную постоянную
-: Отношение силы, с которой поле действует на единичный элемент тока (расположенный параллельно полю в вакууме), к магнитной постоянной
I:
S: Для магнитного поля, создаваемого прямолинейным проводником с током, справедлива формула Ампера, которая записывается в виде
-:
-:
-: 
-: 
+: 
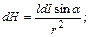
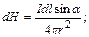
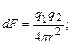
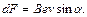
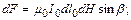
I:
S: Направление силы Ампера определяется по правилу
-: Кирхгофа
-: Буравчика
+: Левой руки
-: Правой руки
-: Ленца
I:
S: Напряженность магнитного поля измеряется в
-: Вольтах
-: Амперах
-: В/м
+: А/м
-: Гауссах
I:
S: Восприимчивость вещества к намагничиванию под действием внешнего магнитного поля называется
-: Магнитной постоянной
-: Индуктивностью среды
-: Диэлектрической проницаемостью среды
-: Магнитной плотностью среды
+: Магнитной проницаемостью среды
I:
S: Для индукции магнитного поля справедливо выражение
+: 
-: 
-: 
-: 
-: 
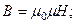
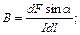
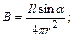
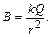
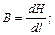
I:
S: Индукция магнитного поля измеряется в
-: Вольтах
-: Амперах
+: Тесла
-: Фарадах
-: Гауссах
I:
S: Выражение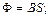 
называется
-: Вектором Умова
+: Потоком индукции
-: Потоком энергии
-: Потоком напряженности
-: Магнитной проницаемостью
I:
S: Поток магнитной индукции измеряется в
-: Вольтах
-: Амперах
-: Тесла
+: Веберах
-: Гауссах
|
|
|
