Интегральная теорема Муавра – Лапласа

Формула Бернулли.

 

При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых один и тот же опыт или аналогичные опыты повторяются неоднократно. В результате каждого опыта может появиться или не появиться событие А, причем нас интересует не результат каждого отдельного опыта, а общее число появлений события А в результате серии опытов. Например, если производится группа выстрелов по одной и той же цели, нас интересует не результат каждого выстрела, а общее число попаданий. Такие задачи решаются достаточно просто, если опыты являются независимыми.

Определение. Независимыми относительно события А испытаниями называются такие, в которых вероятность события А в каждом испытании не зависит от исходов других испытаний.

Пример. Несколько последовательных выниманий карты из колоды представляют собой независимые опыты при условии, что вынутая карта каждый раз возвращается в колоду и карты перемешиваются; в противном случае это – зависимые опыты.

Пример. Несколько выстрелов представляют собой независимые опыты только в случае, если прицеливание производится заново перед каждым выстрелом; в случае, когда прицеливание производится один раз перед всей стрельбой или непрерывно осуществляется в процессе стрельбы (стрельба очередью, бомбометание серией), выстрелы представляют собой зависимые опыты.

Независимые испытания могут производиться в одинаковых или различных условиях. В первом случае вероятность события А во всех опытах одна и та же, во втором случае вероятность события А меняется от опыта к опыту. Первый случай связан со многими задачами теории надежности, теории стрельбы и приводит к так называемой схеме Бернулли, которая состоит в следующем:

1) проводится последовательность n независимых испытаний, в каждом из которых событие А может появиться, либо не появиться;

2) вероятность появления события А в каждом испытании постоянна и равна 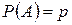, как и вероятность его не появления .

Формула Бернулли, с помощью которой находится вероятность появления события А k раз в n независимых испытаниях, в каждом из которых событие А появляется с вероятностью p:

. (1)

Замечание 1. С возрастанием n и k применение формулы Бернулли связано с вычислительными трудностями, поэтому формула (1) применяется, в основном, если k не превосходит 5 и n не велико.

Замечание 2. В связи с тем, что вероятности по форме представляют собой члены разложения бинома 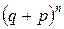, распределение вероятностей вида (1) называется биномиальным распределением.

Пример. Вероятность попадания в цель при одном выстреле равна 0,8. Найти вероятность пяти попаданий при шести выстрелах.

Решение. Так как 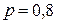, то , кроме того 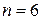и . Пользуясь формулой Бернулли, получим:

 

Пример. Производится четыре независимых выстрела по одной и той же цели с различных расстояний. Вероятности попадания при этих выстрелах равны соответственно:

.

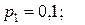
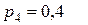Найти вероятности ни одного, одного, двух, трех и четырех попаданий:

 

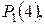
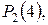
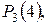
Решение. Составляем производящую функцию:

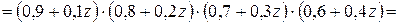
откуда

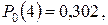
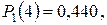
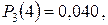
Пример. Производится пять независимых выстрелов по цели, вероятность попадания в которую равна 0,2. Для разрушения цели достаточно трех попаданий. Найти вероятность того, что цель будет разрушена.

Решение. Вероятность разрушения цели вычисляем по формуле:

.

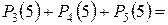
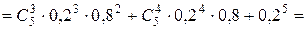
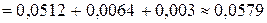Пример. Производится десять независимых выстрелов по цели, вероятность попадания в которую при одном выстреле равна 0,1. Для поражения цели достаточно одного попадания. Найти вероятность поражения цели.

Решение. Вероятность хотя бы одного попадания вычисляем по формуле:

 

 

3. Локальная теорема Муавра-Лапласа

 

В приложениях часто приходится вычислять вероятности различных событий, связанных с числом появлений события в n испытаниях схемы Бернулли при больших значениях n. В этом случае вычисления по формуле (1) становятся затруднительными. Трудности возрастают, когда приходится ещё суммировать эти вероятности. Затруднения при вычислениях возникают также при малых значениях p или q.

Лаплас получил важную приближенную формулу для вероятности появления события А точно m раз, если - достаточно большое число, то есть при .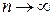

Локальная теорема Муавра – Лапласа. Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы 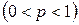, , 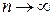величина ограничена равномерно по m и n, то вероятность появления события А ровно m раз в n независимых испытаниях приближенно равна

(4)

где - функция, значения которой определяются таблично.

Замечание. Формулу (4) часто используют пр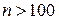и и 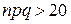, хорошие приближения эта формула дает также при . Указания о границах применимости формулы (4) являются очень приближенными и носят скорее качественный характер: к ним следует относиться с осторожностью. Отметим также, что из того, что 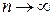следует стремление к бесконечности m. Это значит, что m и n должны отличаться друг от друга не очень сильно, так, для 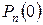локальная теорема дает плохое приближение.

Пример. Вероятность поражения цели при одном выстреле равна 0,3. Найти вероятность того, что при 100 выстрелах цель будет поражена 30 раз.

Решение. Так как , , , , 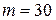то получим:

.

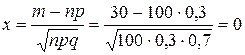Отсюда по формуле (4) имеем:

.

Интегральная теорема Муавра – Лапласа

 

Зададимся вопросом: какова вероятность того, что в условиях схемы Бернулли событие А, имеющее вероятность 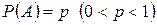, при испытаниях появляется не менее раз и не более 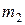раза?

Введем функцию Лапласа:

, (11)

Интеграл не выражается через элементарные функции, для его вычисления используются специальные таблицы. Функция обладает следующими свойствами:

1) ;

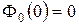2) ;

3) , то есть функция нечетна;

4) 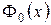- монотонно возрастающая функция;

5) при , с точностью до тысячных, можно принять .

Интегральная теорема Муавра – Лапласа. Если вероятность p появления события А в каждом испытании постоянна и отлична от нуля и единицы 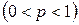, то при 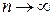вероятность появления события А ровно в n независимых испытаниях не менее раз и не более 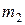раз приближенно равна

(12)

где - функция Лапласа, значения которой определяются таблично, .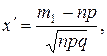

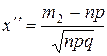Замечание 1. Для того, чтобы можно было пользоваться таблицей функции Лапласа, соотношение (12) преобразуют к виду:

.

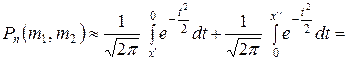
Замечание 2. Функция Лапласа является нечетной функцией . При можно принять .

Пример. Вероятность того, что деталь не прошла проверку ОТК, равна . Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.

Решение. По условию , , , , 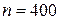. Воспользуемся интегральной теоремой Лапласа:

Найдем

,

.

Таким образом, получим:

.

 

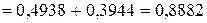Поделиться:

Воспользуйтесь поиском по сайту: