 |
Глава xXVII абстракции высшего порядка
|
|
|
|
Характерные черты, которые наука распознает в природе – это очень тонкие особенности, неочевидные на первый взгляд. Это отношения между отношениями и особенности особенностей. (573) A.N. WHITEHEAD
В связи с этим нужно обратить особое внимание на то, что человеческий язык позволяет конструировать предложения, которые не влекут никаких последствий и, соответственно, вообще не имеют никакого содержания – вопреки тому факту, что эти предложения создают некую картинку в нашем воображении; например, утверждение о том, что кроме нашего мира существует также другой мир, с которым принципиально невозможно установить какую-либо связь, не приводит ни к каким экспериментальным последствиям, но при этом создает в уме некую картинку. Очевидно, подобное утверждение нельзя ни доказать, ни опровергнуть. Особенно осторожно нужно пользоваться словами «реальность», «действительно», и т.п., поскольку эти слова очень часто ведут к возникновению утверждений вышеописанного типа. (215) W. HEISENBERG
Раздел А. Общий.
В предыдущих главах я продемонстрировал, что имеется сокращенное обозначение, которое даёт нам возможность понять, усвоить и применить то, что предлагается в данной работе. Это семантическое сокращенное обозначение – «осознанность абстрагирования». Это психологическая установка в отношении всего нашего абстрагирования на всех уровнях, связанная, соответственно, с согласованной работой организма как целого.
Использование Структурного дифференциала тут является необходимостью, поскольку некоторые уровни несловесны. Мы можем их видеть, осязать, ощущать., но ни при каких обстоятельствах мы не можем достичь этих уровней посредством одной только речи. Поэтому нам нужно иметь диаграмму, предпочтительно в виде наглядного пособия, которая представляет эти эмпирические структурные условия и показывает несловесный уровень другими средствами, не речью. В самом простом случае мы должны либо показывать на объект пальцем, настаивая при этом на безмолвии, либо совершить некое другое телесное движение, точно так же настаивая на безмолвии, так как движения и чувства также не являются словами.
|
|
|
В таком семантическом обучении достаточно настаивать на неотождествлении или на отличии между объективными, несловесными уровнями низших порядков абстракции, (O h), и словесными, или высшими порядками абстракции, (L n). Приобретя эту привычку и это чувство, мы далее не должны сталкиваться с трудностями в распространении метода неотождествления на нашу повседневную жизнь. Для достижения этих семантических целей мы должны сначала подчеркнуть тот основанный на здравом смысле факт, что объект не является событием. Для того, чтобы это сделать, мы начнем с научной структурной «метафизики» события от 1933, и особо выделим тот факт, что объект, будучи нервной абстракцией низшего порядка, имеет меньше м.п характеристик, чем событие, и его характеристики отличаются от характеристик события. Это лучше всего достигается подчеркиванием того факта, что при абстрагировании из события в объект мы опускаем некоторые характеристики. Мы не абстрагируем «все» характеристики; это было бы противоречием в терминах, невозможностью.
Нам даже не требуется подчеркивать полное понимание события. Простых примеров, которые позволяют продемонстрировать это на уровне здравого смысла – скажем, то, что мы узнаем как «карандаш» – это не «всё», тут вполне достаточно. Ни у кого не будет трудностей, при условии, что он обучится в этом направлении, с постоянным и инстинктивным вспоминанием о свободно свисающих нитях (B’), (B’’), которые обозначают неабстрагированные или выпущенные характеристики и помогают натренироваться в неотождествлении.
|
|
|
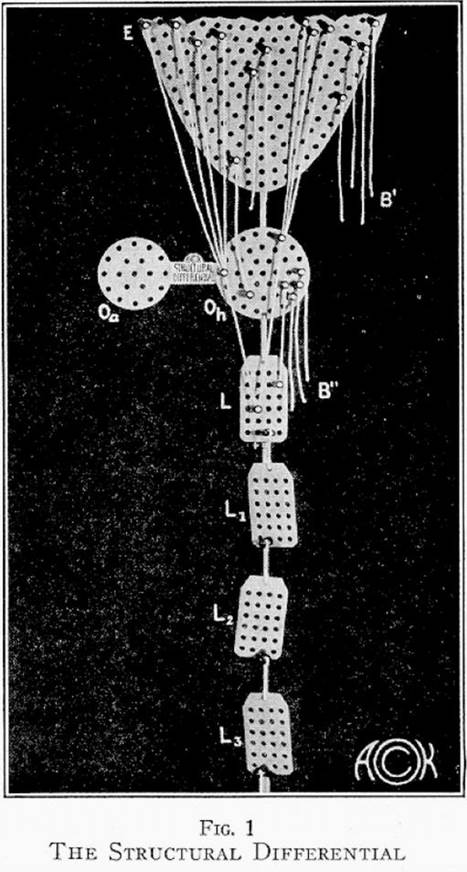
С помощью наглядного пособия с.р студента тренируются через все нервные центры. Он видит, осязает., свисающие нити, а также слышит о них. Это дает максимальную вероятность того, что воздействие будет оказано на организм как целое. Таким образом «интеллектуальная» теория задействует механизмы «чувств», ощущений и рефлексов. Для воздействия на организм как целое нужно использовать целостные методы.
Подобная же структурная ситуация обнаруживается при работе с абстракциями высшего порядка. Слово, название или утверждение передается в устной или письменной форме, и сначала воздействует на низшие центры, а потом абстрагируется и преобразуется далее высшими центрами. В общем, такой порядок не меняется и справедлив для случая, когда устные вопросы невидимы и неслышимы, а производятся внутри нас самих. Большинство «импульсов», «интересов», «смыслов», «оценок»., производятся в низших центрах и следуют обычным курсом от низших центров к высшим. Когда «переживание» (реакция низших центров) преобразуется в «воспоминание» (высшие центры)., порядок также подобный. Трудности возникают тогда, когда этот порядок патологически обращается и «идеи» начинают оцениваться как опыт, слова как объекты,. В построении языка можно наблюдать похожий процесс. Мы наблюдаем абсолютных индивидуумов, с которыми мы действительно имеем дело, обозначаем их индивидуальными названиями, скажем, A1, A2,..., A11, A12,..., A21, A22,..., A31, A32,...,. Через процесс абстрагирования и игнорирования, например, характеристик, обозначенных индексом «1», мы можем оставить только те, которые обладают характеристиками с индексами 2, 3,..., 9, 22, 23,..., 29,. Проигнорировав характеристики с индексом «2», мы оставим только те, что обозначены как 3, 4,.... 9, 33, 34...., 39,. Наконец, если мы исключим все индивидуальные характеристики и индексы, то получим «общее» название А для всей группы, не выделяя в ней никаких индивидуальных характеристик.
Все слова типа «человек», «животное», «дом», «стул», «карандаш»., были построены подобным процессом абстрагирования, или игнорирования, индивидуальных отличий. В каждом случае игнорирования индивидуальных характеристик был задействован новый нейрологиче-ский процесс.
|
|
|
Подобное же происходит с «утверждениями об утверждениях». Когда мы слышим некое утверждение или видим его в письменной форме, оно становится стимулом, который поступает через низшие центры, и утверждение о нем представляет собой, вообще говоря, новый процесс абстрагирования, или абстракцию высшего порядка.
Становится очевидно, что введение языка «различных порядков абстракции», хотя он и не является привычным, тем не менее структурно весьма близко соответствует в терминах порядка наиболее фундаментальным нейрологическим процессам, которые происходят в нас. Как нам уже известно, естественный порядок был установлен эволюцией; а именно: сначала абстракции низшего порядка, потом высшего; отождествление порядков или обращение порядков представляется для человека патологией и проявляется как смешивание порядков абстракций, которое приводит к ложной оценке: отождествлению, иллюзиям, бреду и галлюцинациям.
Исторически первыми, кто обратил серьезное внимание на вышеописанную проблему систематическим образом, хоть и в ограниченном объеме, были математики. При исследованиях проблем фундаментальных основ математики, математической «логики» и теории множеств, мы натолкнулись на противоречия, которые сделали бы математику невозможной. Во избежание этой беды Рассел (Russell) изобрел нечто, названное им «теорией математических типов». Статус этой теории очень интересен и поучителен. Эта теория решает математические трудности, спасая таким образом математику, но у нее нет никакого применения в жизни. Практически все математики, если я не ошибаюсь, включая самого автора теории, как-то «не любят» эту теорию и стараются решать задачи другими способами и по возможности вообще избегать этой теории.
Мы уже показали, что введение языка «различных порядков абстракции» структурно полностью обоснованно и физиологически естественно, поскольку он описывает в терминах «порядка» деятельность нервной системы. Такие факты важны; но если, кроме того, введение языка новой Ā структуры позволит нам и далее демонстрировать его преимущества, то введение такого языка стало бы всё более желательным.
|
|
|
Несмотря на то, что большинство математиков «не любит» теорию типов, эта теория, тем не менее, безусловно является необходимой для несамопротиворечивой математики. Автор был приятно удивлен, обнаружив, что после того, как была сформулирована его Ā -система, эта простая и естественная, действенная, функциональная, применимая, нон-эл теория оказалась перекрывающей и обобщающей теорию математических типов, делая эту теорию применимой не только в области решения математических парадоксов, но также в отношении большинства чисто человеческих и научных проблем. Одно общее правило «несмешивания порядков абстракций» и приобретение простой и полезной «осознанности абстрагирования», основанной на отказе от отождествляющего «есть», предоставляет полное структурное и семантическое решение. Игнорирование связанных с этим вопросов неизбежно приводит к возникновению бесконечных и никому не нужных человеческих страданий и бед, устранение которых является одним из основных моментов теории психического здоровья. В 1933 году не является тайной то, что постоянное получение небольших болезненных шоков может привести к серьезным семантическим и физическим расстройствам. Психо-логикам и психиатрам будет всё труднее и труднее работать над стоящими перед ними проблемами, если они продолжат игнорировать эти семантические моменты. Родители и учителя обнаружат простые, но очень эффективные структурные средства для тренировки здоровых реакций у детей, со всеми соответствующими семантическими выгодами для людей и для общества.
Когда Уайтхед (Whitehead) и Рассел (Russell) работали над основаниями математики, они столкнулись с бесконечными парадоксами и противоречиями в себе, которые, конечно, сделали бы математику невозможной. Приложив множество усилий, они обнаружили, что у этих всех парадоксов был один общий источник, грубо говоря - выражения, которые содержали слово «все», и решение было найдено во введении «невсеобщности», семантического предшественника неотождествления. Рассмотрим для примера «утверждение обо всех утверждениях». Они обнаружили, что подобные обобщения, или «общие» утверждения, были незаконными, поскольку они с самого начала противоречили самим себе. Невозможно законным образом сделать утверждение обо «всех» утверждениях без какого-либо ограничения, поскольку оно бы включило в себя и это новое только что сделанное утверждение. Если рассмотреть м.п термин, такой как «утверждение», а таковые мы можем производить безо всякого ограничения, и вспомнить о том, что любое утверждение об утверждениях принимает форму утверждения, то, очевидно, мы не можем делать утверждения обо всех утверждениях. В подобных случаях это утверждение должно быть ограничено; у такого набора нет общей суммы, и утверждение обо «всех его членах» нельзя сделать законным образом. Подобным же образом, мы не можем говорить обо всех числах.
|
|
|
Утверждения типа «утверждения обо всех утверждениях» были названы Расселом «незаконными обобщениями». В подобных случаях необходимо подразделить данный набор на более мелкие наборы, каждый из которых может быть обобщен. В общих чертах это и есть суть формулировки цели теории типов. На языке Principia Mathematica тот принцип, который дает нам возможность избежать незаконных обобщений, можно выразить следующим образом: «То, что касается всего множества, не должно являться одним из этого множества», или «Если, при условии, что у определенного множества есть общая сумма, в нем найдутся члены, определимые только в терминах этой общей суммы, то у рассматриваемого множества нет никакой общей суммы». 1 Вышеуказанный принцип называется «принципом порочного круга», поскольку он позволяет нам избавиться от порочных кругов, которые порождаются введением незаконных обобщений. Рассел называет споры, которые связаны с принципом порочного круга», «заблуждениями порочного круга».
В качестве примера Рассел дает двузначный закон «исключенного третьего», сформулированный в виде «все утверждения являются либо истинными, либо ложными». Мы впадаем в заблуждение порочного круга, если начинаем утверждать, что закон исключенного третьего принимает форму утверждения, и, следовательно, может оцениваться как истинный или ложный.
Прежде чем мы сможем сделать какое-либо утверждение обо «всех утверждениях» законным, нам нужно ограничить его некоторым образом, так, чтобы утверждение об этом множестве не входило в само это множество.
Другим примером заблуждения порочного круга может послужить некий воображаемый скептик, который заявляет, что он ничего не знает, и в ответ получает опровергающий вопрос -а знает ли он, что он ничего не знает! Прежде чем заявление этого скептика станет значимым, он должен неким образом ограничить количество фактов, в отношении которых он проявляет свое «невежество», иначе он сделает незаконное обобщение. Когда же такое ограничение наложено, и он заявляет, что он невежественен в отношении экстенсиональной последовательности утверждений, и его утверждение о собственном невежестве не является членом этой последовательности, то подобный скептицизм опровергнуть подобным образом невозможно.
У нас нет надобности погружаться в дальнейшие подробности сложной и трудной теории типов. В моей А психофизиологической формулировке эта теория становится структурно крайне простой и естественной, и она применима как к математике, так и к большому количеству повседневных переживаний, устраняя невероятно большое число непониманий, порочных кругов и прочих семантических источников человеческих несогласий и несчастий.
Следует отметить, что в приведенных примерах мы всегда делали утверждение о другом утверждении, и что полученный порочный круг возникал из-за отождествления или смешивания порядков данных утверждений. Выход обнаруживается в виде «осознанности абстрагирования», которая дает семантическое различение между порядками абстракций. Если у нас есть определенные предпосылки, р\, р2, рз,... pn, и мы строим новую предпосылку об этих предпосылках, скажем, Р, то, в соответствии с представленной теорией, предпосылка Р о предпосылках р\,рг., должна рассматриваться как абстракция более высокого порядка, другого порядка, который не должен отождествляться с порядком предпосылок р\,рг, ■ ■ Р-п-
Приведенная выше психофизиологическая формулировка является совершенно общей, но при этом простой и естественной в рамках /-системы. Для того, чтобы сделать это более ясным, я возьму несколько утверждений касательно теории типов из Principia Mathematica, обозначив их как (Рг.), и переформулирую их на моем языке порядков абстракций, обозначив их сокращением для общей семантики (G. S.).
Так, «Рассматриваемые порочные круги появляются из предположения о том, что совокупность объектов может содержать члены, которые определимы только посредством данной совокупности как целого» (Рг.). Объекты как индивидуумы и как «обобщение объектов», очевидно, принадлежат к различным порядкам абстракций, которые не следует смешивать (G.S.). «Утверждение обо всех утверждениях» (Рг.). Это связано со смешиванием порядков абстракций, поскольку, если мы сформулируем утверждения р\, рг,... рп, то утверждение Р об этих утверждениях будет представлять собой абстракцию высшего порядка, которую не следует с ними отождествлять (G.S.). «Более общо, рассматривая любой набор объектов, подобный данному, если мы предположим, что у данного набора есть общая сумма, и при этом в нем найдутся члены, определимые только в терминах этой общей суммы, то у рассматриваемого набора нет никакой общей суммы. Говоря о том, что у набора нет «общей суммы», мы имеем в виду, что «обо всех его членах» невозможно сделать какое-либо осмысленное утверждение». (Рг.). Набор утверждений, объектов или элементов, или чего-то подобного, и утверждение о них относятся к разным порядкам абстракций, и их не следует смешивать (G.S.). На языке Виттгенштейна (Wittgenstein): «Никакое утверждение не может ничего сказать о себе, поскольку предпосылка не может следовать из себя самой (это «вся суть теории типов).»2
На языке современной общей семантики утверждение об утверждении не является «таким же» утверждением, но представляет собой, по структурной и нейрологической необходимости, более высокий порядок абстракции. И его не следует путать с исходным утверждением.
Подобные переформулировки относятся ко всем случаям, приведенным в Principia Mathematica, так что становится очевидно, что представленная теория охватывает ту же территорию, что и теория типов, а также бесконечный список повседневных жизненных проблем, которые несут критическую семантическую важность для теории психического здоровья. Здесь мы должны особо указать на простой, естественный и единственный семантический закон нетождественности, который охватывает все смешивания порядков абстракций. Это одно правило, а также тренировки, учат нас не смешивать высшие абстракции с низшими, не отождествлять слова с объектами (не объектифицировать), а также не смешивать высшие абстракции разных порядков. Эта обобщенность и структурная простота являются весомым аргументом в пользу представленной Ā -системы. Преподавать простое, единственное и естественное правило, которое перекрывает огромную область семантических источников человеческих трудностей, гораздо проще. Ибо как только данное правило объяснено, и ученик потренировался со Структурным дифференциалом, семантическая проблема разрешается просто показыванием пальцем на «различные порядки абстракций», и настаиванием на том, что «это не есть это».
Если рассмотреть естественный, структурный и эмпирический факт о том, что наши жизни проживаются в мире неотождествляемых абстракций разных порядков, различение между этими различными порядками обретает первостепенную семантическую важность для оценки. При таких условиях нам следует тщательно разобраться с механизмом этих различных порядков абстракций. Во-первых, следует отметить, что язык Principia Mathematica является A, и содержит отождествляющее «есть»,. Такой язык приводит к отождествлениям и замешательствам, делая простые вопросы трудными и парадоксальными. Термин «класс» сам по себе запутывает. Что мы имеем в виду под этим термином? В жизни у нас есть только индивидуальные вещи на объективных, несловесных уровнях. Если мы возьмем некоторое их количество, то у нас их будет несколько, но каждая из них сохранит индивидуальность. Если мы производим абстракцию высшего порядка, при потере индивидуальности каждого члена, то у нас получается абстракция высшего порядка (на старом языке, «идея»), и у нас больше нет тех абсолютных индивидуумов из нашего набора. Термин «класс» в этом отношении вводит в серьезное замешательство, поскольку он склонен опускать простой экспериментальный факт, и он приводит к смешиванию порядков абстракций, если не сформулировать многопорядковость термина «класс».
Многие критики и рецензенты Principia Mathematica так или иначе понимали, что это так, но их критика была не слишком уверенной и не добиралась до корней этой A семантической трудности. Они не обращают внимания на A, «логический», «философский» и «психологический» элементалистский метод и язык, построенный на отождествляющем «есть», на котором написано введение в Principia. Доктор Алонсо Черч (Alonzo Church) является первым, насколько мне известно, кто предположил, что, следуя идеям Пеано (Peano), числа следует определять на языке абстракций. Однако он не продолжает этот анализ далее и не говорит о том, что для этого требуется язык с совершенно иной Ā структурой.3 Если отказаться от термина «класс» и принять язык «абстракций различных порядков», то мы придем далее к отказу от отождествляющего «есть» и к представленной здесь системе, в которой теория математических типов становится необходимой частью. Проблемы «класса» перестают быть «предположением», так как различные порядки абстракций являются описанием экспериментальных фактов; так что «аксиома сводимости» становится ненужной. На моем языке, данная аксиома также является аристотелевым описанием того экспериментального факта, что мы можем абстрагировать на различных порядках.
Раздел B. Многопорядковые термины.
В примерах в Разделе А мы использовали такие слова, как «утверждение», которые применимы ко всем абстракциям высшего порядка. Мы уже видели, что подобные термины могут иметь разные применения и значения при использовании на разных порядках абстрагирования. Это порождает явление, которое я называют многопорядковость терминов. Слова «да», «нет», «истинный», «ложный», «функция», «свойство», «отношение», «число», «различие», «название», «определение», «абстракция», «утверждение», «факт», «реальность», «структура», «характеристика», «проблема», «знать», «думать», «говорить», «ненавидеть», «любить», «сомневаться», «причина», «следствие», «значение», «оценка» и бесконечный набор наиболее важных терминов, которые у нас есть, нужно рассматривать как многопорядковые термины. У этих м.п терминов есть одна наиболее важная семантическая характеристика: они неоднозначны, или ∞- значны, и у каждого появляется некое определенное значение или смысл только и исключительно при наличии конкретного контекста, когда можно определенно указать порядок абстракции.
Эти вопросы представляются крайне простыми и общими, они являются неотъемлемой частью структуры «человеческого знания» и нашего языка. Мы не можем игнорировать эти семантические вопросы и, соответственно, остается только один выход – явным образом разобраться с ними. Тест на многопорядковость термина прост. Давайте сделаем любое утверждение и посмотрим, применим ли к нему данный термин («истинный», «ложный», «да», «нет», «факт», «реальность», «думать», «любить»,.). Если да, давайте намеренно сделаем другое утверждение о предыдущем утверждении, и проверим, можно ли снова использовать тот же самый термин. Если это так, можно уверенно предположить, что данный термин следует рассматривать как м.п. Каждый может безо всяких трудностей самостоятельно протестировать подобный м.п термин. Главный момент по поводу всех подобных м.п терминов состоит в том, что, в общем, они неоднозначны, и все споры о них, «в общем», приводят только к отождествлению порядков абстракций и семантическим расстройствам, и больше ни к чему. Многопорядковые термины обладают определенным значением только на данном уровне и только при заданном контексте. Прежде чем начинать о них спорить, нужно зафиксировать их порядки, после чего все вопросы станут простыми, и возникнет согласие. Что касается «порядков абстракции», у нас тут нет возможности убедиться в «абсолютном» порядке абстракции; кроме того, это никогда и не требуется. В человеческих семантических трудностях, в науке, а также в частной жизни, обычно требуется рассматривать не более чем три, может быть, даже два, соседних уровня. Когда дело касается серьезного обсуждения некой проблемы, из-за смешивания соседних уровней или их отождествления возникают ошибки, неоднозначности, замешательства и разногласия. На практике разобраться с этими тремя (или двумя) уровнями и разделить их можно крайне просто – при условии, что мы осознаем абстрагирование, но только при этом условии.
Для теории психического здоровья эти вопросы представляются важными и существенными структурно. В отождествлениях, бреде, иллюзиях и галлюцинациях мы обнаружили смешивание порядков абстракций, или ложную оценку, выраженную в виде обращения естественного порядка.
Один из симптомов этой путаницы проявляется в виде «ложных убеждений», которые, опять же, подразумевают сравнение утверждений о «фактах» и «реальности», и связаны с такими терминами, как «да», «нет», «истинный», «ложный»,. Поскольку все эти термины многопорядковые, и, следовательно, неоднозначные, следует избегать «философской» болтовни «об этом вообще». С осознанностью абстрагирования и, следовательно, с чувством в отношении этого особенного расслоения «человеческого знания», все семантические проблемы можно решить довольно просто.
Невозможно и нежелательно избегать м.п терминов. Систематическая неоднозначность большинства важнейших терминов происходит в соответствии с систематической аналогией. Они появляются как непосредственный результат и условие нашей способности абстрагировать на различных порядках, и позволяют нам применять одну цепочку ∞-значной логики к бесконечному набору различных однозначных фактов, каждый из которых отличается ото всех остальных и становится управляемым только благодаря нашей абстрагирующей способности.
Более подробное описание теории типов читатель может найти в ссылках на литературу по предмету и в Приложении II4; здесь же я только приведу несколько примеров сложностей и трудностей, встроенных в язык, и покажу, как просто они решаются с помощью Ā общей семантики и проистекающей из нее «осознанности абстрагирования».
Для примера я процитирую анализ Рассела «простого» утверждения «я лгу», приведенный в Principia. «Старейшее противоречие подобного рода известно по имени Эпименида. Эпименид Критский сказал, что все критяне – лжецы, и что все утверждения, сделанные критянами, определенно являются ложными. Было ли это утверждение ложью? Простейшая форма данного противоречия предоставляется человеком, который говорит «Я лгу»; если он лжет, то он говорит правду, и наоборот....
«Когда человек говорит «Я лгу», можно истолковать его утверждение как: «Есть утверждение, которое я высказываю, и которое является ложным». То есть, он утверждает истинность некоторой ценности функции «я утверждаю p, и p является ложным». Но мы видели, что слово «ложный» является неоднозначным, и что для того, чтобы сделать его однозначным, нужно конкретизировать порядок этой ложности, или, что то же самое, порядок утверждения, которому приписывается ложность. Мы также видели, что, если p является утверждением n -ного порядка, то утверждение, в котором p, очевидно, является переменной, не принадлежит к n -ному порядку, а имеет более высокий порядок. Следовательно, истинность или ложность, которые могут относиться к утверждению «имеется утверждение p, которое я утверждаю и которое обладает ложностью n -ного порядка» – это истинность или ложность более высокого порядка, чем n-ный. Следовательно, утверждение Эпименида не относится к самому себе, и, соответственно, не возникает никакого противоречия.
«Если мы рассмотрим утверждение «Я лгу» как компактный способ одновременно сделать все следующие утверждения: «Я высказываю ложное утверждение первого порядка», «Я высказываю ложное утверждение второго порядка», и так далее, то мы обнаружим следующее любопытное состояние дел: по причине отсутствия высказанного утверждения первого порядка, утверждения «Я высказываю ложное утверждение первого порядка» является ложным. Это утверждение принадлежит ко второму порядку, следовательно, утверждение «Я делаю ложное утверждение второго порядка» является истинным. Это утверждение третьего порядка, и оно является единственным утверждением третьего порядка, которое делается. Следовательно, утверждение «Я делаю ложное утверждение третьего порядка» является ложным. Так, мы видим, что утверждение «Я делаю ложное утверждение порядка 2 n +1» является ложным, в то время как утверждение «Я делаю ложное утверждение порядка 2 n» истинно. При таком положении дел никакого противоречия не наблюдается».5
Понятно, что если применить язык порядков абстракций к вышеописанному случаю, то подобный вывод можно сделать в более обобщенном и простом виде. Если смешивать порядки абстракций, то, естественно, из этого выйдет бесконечный спор. Этот пример показывает, как смешивание порядков абстракций может привести к нерешаемым словесным проблемам, и как семантически важно то, что не следует отождествлять и нужно быть осознающим абстрагирование, с проистекающим из этого инстинктивным чувством этого особенного структурного расслоения «человеческого знания». Следует отметить, что при смешивании порядков абстракций и использовании м.п терминов, без осознания их ∞-значного характера, всегда можно создать бесконечный набор подобных словесных споров, которые будут затемнять данный вопрос, но как только мы припишем м.п терминам определенный порядок и тем самым установим конкретное единственное значение для данного контекста для множества значений, которыми может обладать любой м.п термин, все трудности пропадут.
Поскольку вышеприведенный анализ относится ко всем м.п терминам, а эти термины являются наиболее важными в нашей жизни, нет никакого смысла в попытках избегать этих терминов или последствий их использования. Как раз наоборот; часто возникает структурная необходимость в построении м.п термина – например, «абстрагирование» – где мы должны принять за данность то, что он обладает множеством значений, и указать на эти значения, придавая этому термину определенный порядок абстракции. Так, такие термины, как «абстрагирование» или «характеристика»., можно рассматривать как путаные или вводящие в замешательство; но «абстрагирование на различных порядках»., таким не будет, поскольку в конкретном контексте всегда можно приписать данному термину определенный порядок и единственное значение.
Уже несколько раз повторялось, что м.п термин, по структурной необходимости, обладает множеством значений. Независимо от того, как мы его определим, его определение, опять же, основано на других м.п терминах. Если мы попытаемся дать м.п термину общее «значение», которым он обладать не может, дальнейший и более глубокий анализ раскрыл бы многопорядко-вость терминов, которыми он определяется, что снова бы восстановило его многопорядковость. Поскольку возможности избежать вышеописанного вопроса нет, было бы правильнее, а также удобнее сразу признать фундаментальную многопорядковость термина. И если мы это сделаем, мы не будем путаться в отношении значения подобного термина в данном контексте, потому что, в принципе, в контексте его значение является единственным, оно этим контекстом зафиксировано. Семантические выгоды такого признания многопорядковости, в основном, сводятся к семи категориям: (1) мы экономим огромное количество «времени» и усилий, поскольку мы прекращаем «охоту на снарка», обычно называемую «философией», или на однозначное общее определение м.п термина, которое не было бы сформулировано другими м.п терминами; (2) мы обретаем большую гибкость в самовыражении, поскольку наш наиболее важный словарный запас состоит из м.п терминов, и его можно бесконечно расширять за счет назначения множества различных порядков и, следовательно, значений; (3) мы признаем то, что определение м.п термина должно, с необходимостью, представлять собой не утверждение, а функцию в отношении утверждений, построенную на переменных; (4) нам не требуется особенно беспокоиться о формальном определении м.п термина вне рамок математики, но мы можем свободно пользоваться им, осознавая его уникальное, в принципе, значение в данном контексте, которое структурно фиксируется имеющимся контекстом; (5) при таких структурных условиях, свобода писателей и ораторов обретает особую широту; их словарный запас состоит, потенциально, из бесконечного количества слов, и психо-логическая, семантическая блокада при этом устраняется; (6) они знают, что читатель, который понимает этот ∞-значный механизм, никогда не впадет в замешательство в отношении смысла, который вкладывался в то или иное высказывание; и (7) весь лингвистический процесс становится крайне гибким, при этом сохраняя свой существенный однозначный характер для конкретных случаев.
В определенном смысле, подобное применение м.п терминов можно обнаружить в поэзии, и хорошо известно, что многие ученые, особенно те, кто увлекается творчеством, любят стихи. Более того, поэзия часто в нескольких словах передает больше вечных ценностей, чем целый том научного анализа. Свободное использование м.п терминов, без необходимости волноваться о структурно невозможном вне рамок математики формализме, достигает этой цели, при условии, что мы осознаем абстрагирование; в противном же случае возникает одно лишь замешательство.
Следует понимать, что у меня нет намерения осуждать формализм. Формализм наиболее строгого характера является дисциплиной крайне важной и ценной (на данный момент это математика); но формализм как таковой в экспериментальной науке и в жизни часто становится препятствием, а не помогает, потому что в эмпирической науке и жизни мы занимаемся исследованием и открытием неизвестной структуры мира с целью структурной адаптации. Формальное рассмотрение любого языка сводится лишь к последовательному разбору его структуры, который должен проводиться независимо, если мы хотим получить средства для сравнения словесной и эмпирической структур. С Ā точки зрения оба вопроса одинаково важны для исследования структуры.
При таких структурных эмпирических условиях м.п термины приобретают большую семантическую важность, и, возможно, без них язык, математика и наука вообще были бы невозможны. Как только мы понимаем это, мы вынуждены осознать глубокую структурную и семантическую разницу между A и Ā системами. То, что прежде считалось утверждениями, становится функциями от утверждений, и большинство наших доктрин становятся доктринальными функциями Кейсера (Keyser), или системными функциями, позволяющими множественные толкования.
Термины принадлежат к словесным уровням, и их значения должны даваться определениями, а определения зависят от неопределяемых терминов, которые всегда, насколько я знаю, представляют собой м.п термины. Возможно, для того чтобы вообще быть полезными, они должны обладать таким характером. Принимая в расчет эти структурные эмпирические условия, мы должны сделать вывод, что постуляционный метод, который дает структуру конкретной доктрины, лежит в основании всех человеческих лингвистических действий, как в повседневной жизни, так и в математике и науке. Изучение этих проблем проливает наиболее важный свет на все тайны языка, и на надлежащее использование этой самой важной человеческой нейрологической и семантической функции, без которой психическое здоровье невозможно.
Со структурной точки зрения, постулаты, определения или предположения должны рассматриваться как те устанавливающие отношения или многомерные порядковые структурные предположения, которые определяют, вместе с неопределяемыми терминами, структуру данного языка. Очевидно, для выявления структуры языка нужно проработать данный язык до получения системы постулатов и обнаружения минимального набора его (не являющихся уникальными) неопределяемых терминов. Сделав это, мы должны увидеть перед собой полностью раскрытую систему; далее, обладая тщательным знанием структуры данного языка, мы обретаем крайне ценный инструмент для исследования эмпирической структуры через словесное предсказание и последующую эмпирическую проверку.
Чтобы успокоить неспециалистов, позвольте мне сразу сказать, что такая работа является очень трудоемкой и нелегкой, хоть и представляет собой насущную необходимость; тем не менее, она может быть выполнена одним индивидуумом. Однако по причине характера данной проблемы, когда такая работа сделана, семантические результаты каждый раз до сих пор оказывались – и, вероятно, так будет и в будущем, – довольно простыми и приемлемыми даже для здравого смысл
|
|
|


