 |
Определенный интеграл как предел интегрально суммы.
|
|
|
|
Интегрирование по частям. замена переменной
Метод замены переменной
Пусть функция у = f(х) непрерывна на отрезке [a, b], а функция x=φ(t), определена на отрезке [α, β] и имеют на нем непрерывную производную, причем φ (α) = а, φ (β) = b и для всех  . Тогда
. Тогда

Метод интегрирования по частям
Если функции u = u(x), v = v(x) имеют непрерывные производные на отрезке [a, b], то справедлива формула
 Доказательство.
Доказательство.
Поскольку функция u(x)v(x) – первообразная для функции u’(x)v(x) + u(x)v’(x), то

откуда и следует формула  которую можно записать в виде
которую можно записать в виде

определенный интеграл как предел интегрально суммы.
Пусть функция у = f(x) определена на отрезке [ а;b ], a < b. Выполним следующие действия.
1.С помощью точек  разобьем отрезок [ а, b ] на n частичных отрезков
разобьем отрезок [ а, b ] на n частичных отрезков  (см. рис.).
(см. рис.). 
2.В каждом частичном отрезке  выборем произвольную точку
выборем произвольную точку  и вычислим значение функции в ней. т.е. величину
и вычислим значение функции в ней. т.е. величину  .
.
3.Умножим найденное значение функции  на длину
на длину  соответствующего частичного отрезка:
соответствующего частичного отрезка:  .
.
4.Составим сумму  всех таких произведений:
всех таких произведений:
 Сумма вида (35.1) называется интегральной суммой функции у = f(x) на отрезке [ а; b ]. Обозначим через
Сумма вида (35.1) называется интегральной суммой функции у = f(x) на отрезке [ а; b ]. Обозначим через  длину наибольшего частичного отрезка:
длину наибольшего частичного отрезка: 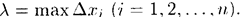
5.Найдем предел интегральной суммы (35.1). когда n→∞ так, что λ→0.
Если при этом интегральная сумма  имеет предел I, который не зависит ни от способа разбиения отрезка [ a; b ] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции у = f{x) на отрезке [ а; b ] и обозначается
имеет предел I, который не зависит ни от способа разбиения отрезка [ a; b ] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции у = f{x) на отрезке [ а; b ] и обозначается  . Таким образом,
. Таким образом,  Числа a и b называются соответстиенно нижним и верхним пределами интегрирования, f(x) — подынтегральной функцией, f(x)dx — подынтегральным выражением, х — переменной интегрирования.
Числа a и b называются соответстиенно нижним и верхним пределами интегрирования, f(x) — подынтегральной функцией, f(x)dx — подынтегральным выражением, х — переменной интегрирования.
отрезок [ а; b ] — областью (отрезком) интегрирования.
Функция у = f(x), для которой на отрезке [ a; b ] существует определенный интеграл  , называется интегрируемой на этом отрезке.
, называется интегрируемой на этом отрезке.
Сформулируем теперь теорему существования определенного интеграла.
Теорема Коши. Если функция у = f(x) непрерывна на отрезке [ a; b ], то определенный интеграл  существует.
существует.
|
|
|
Отметим, что непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.
Укажем некоторые свойства определенного интеграла, непосредственно вытекающие из его определения (35.2).
Определенный интеграл не зависит от обозначения переменной интегрирования:
 Это следует из того, что интегральная сумма (Коши), а следовательно, и ее предел (35.2) не зависят от того, какой буквой обозначается аргумент данной функции.
Это следует из того, что интегральная сумма (Коши), а следовательно, и ее предел (35.2) не зависят от того, какой буквой обозначается аргумент данной функции.
2.Определенный интеграл с одинаковыми пределами интегрирования равен нулю:
 3. Для любого действительного числа с:
3. Для любого действительного числа с: 
65. геометрический смысл. определенного интеграла.
Пусть ф-я  определена на отрезке
определена на отрезке  . Разобьём отрезок
. Разобьём отрезок  точками
точками  . Длина каждого
. Длина каждого 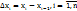 . Выберем в каждом из частичных отрезков точку
. Выберем в каждом из частичных отрезков точку  .
.
Рассмотрим сумму  Эта сумма наз. частично интегральной суммой ф-и
Эта сумма наз. частично интегральной суммой ф-и  на отрезке
на отрезке  . Геометрически сумма
. Геометрически сумма  предст. собой алгебраич. сумму площадей прямоугольников, в основании кот. лежат отрезки
предст. собой алгебраич. сумму площадей прямоугольников, в основании кот. лежат отрезки  , а высоты равны
, а высоты равны  .
.
Предел интегральной суммы  , найденный при условии, что длина наибольшего частичного отрезка стрем. к 0, (мелкость разбиения стрем. к 0) наз. определённым интегралом функции
, найденный при условии, что длина наибольшего частичного отрезка стрем. к 0, (мелкость разбиения стрем. к 0) наз. определённым интегралом функции  в пределах от
в пределах от  до
до 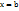

Теорема: если ф-я  непрерывна на
непрерывна на  , то она интегрируема на
, то она интегрируема на  , т.е. предел интегральной суммы существует и не зависит от способа разбиения отрезка
, т.е. предел интегральной суммы существует и не зависит от способа разбиения отрезка  на частичные отрезки
на частичные отрезки  и выбора на них точек
и выбора на них точек  .
.
Если  на
на  , то геометрически опр. интеграл выражает площадь фигуры, ограниченной графиком
, то геометрически опр. интеграл выражает площадь фигуры, ограниченной графиком  , осью ОХ и двумя прямыми
, осью ОХ и двумя прямыми  и
и 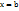 , называемый криволинейной трапецией.
, называемый криволинейной трапецией.
|
|
|
Свойства определённого интеграла:
1. 
2. 
3. 
4. 
5.  , то
, то 
6. 
7. 
8.  ,
,  , то
, то 
9. 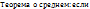 ф-я
ф-я  непрерывна на отрезке
непрерывна на отрезке  ,
,  ,то на этом отрезке сущ. хотя бы одна точка
,то на этом отрезке сущ. хотя бы одна точка  ,
,  такая, что
такая, что 
10.  −я
−я  непрерывна и
непрерывна и 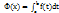 ,то имеет место равенство
,то имеет место равенство  Ф-я
Ф-я  наз. определённым интегралом с переменным верхним пределом.
наз. определённым интегралом с переменным верхним пределом.
11.  Ньютона-Лейбница: если
Ньютона-Лейбница: если  - какая-либо первообразная от
- какая-либо первообразная от  , то
, то 
Формула Ньютона-Лейбица.
Введем сначала понятие определенного интеграла с переменным верхним пределом.
Рассмотрим функцию у = ƒ(х), интегрируемую на отрезке [a, b]. Если х  [a, b], то функция ƒ(х) интегрируема также на любом отрезке [a, x]. Предположим, что х меняется на отрезке [a, b], тогда на этом отрезке определена функция
[a, b], то функция ƒ(х) интегрируема также на любом отрезке [a, x]. Предположим, что х меняется на отрезке [a, b], тогда на этом отрезке определена функция

Докажем, что функция  непрерывна на отрезке [a, b]. Аргумент х придадим приращение
непрерывна на отрезке [a, b]. Аргумент х придадим приращение  такое, что
такое, что  [a, b], тогда по свойству 1 определенного интеграла получим
[a, b], тогда по свойству 1 определенного интеграла получим
 Применяя теорему о среднем, находим
Применяя теорему о среднем, находим

где  m – наименьшее, М – наибольшее значение функции ƒ(х) на отрезке (х, х + + Δх]; эти значения существуют, так как функция интегрируема, следовательно, и ограничена.
m – наименьшее, М – наибольшее значение функции ƒ(х) на отрезке (х, х + + Δх]; эти значения существуют, так как функция интегрируема, следовательно, и ограничена.
Из двух последних равенств следует, ΔФ = μΔх, откуда ΔФ→0 при Δх→0, т.е. Ф(х) – неравная функция, о чем свидетельствует следующая теорема.
Теорема
Если подынтегральная функция непрерывна, то производная определенного интеграла с переменным верхним переделом существует и равна значению подынтегральной функции для этого предела, т.е.
Ф’(х) = ƒ(х).
Доказательство.
Аргументу х функции  придадим приращение Δх такое, что
придадим приращение Δх такое, что  [a, b], ему соответствует приращение функции
[a, b], ему соответствует приращение функции

Применяя формулу  получаем
получаем  = х + θΔх, 0< θ<1.
= х + θΔх, 0< θ<1.
Итак, ΔФ = ƒ(ξ)Δх, откуда
 θΔх) = ƒ(х), т.е.
θΔх) = ƒ(х), т.е.
 или
или 
что и требовалось доказать.
Следствие. Определенный интеграл верхним пределом является одной из первообразных для непрерывной подынтегральной функции. Другими словами, для любой непрерывной на промежутке функции существует первообразная.
Формула Ньютона – Лейбница.
Формула Ньютона – Лейбница связывает неопределенный и определенный интегралы.
Если функция y=f(x) непрерывна на отрезке [a,b],а функция F(x)—какая-л. ее первообразная (т.е. F’(x)=f(x)), то 
|
|
|
|
|
|


