 |
Вопрос №8. Правило выводимости.
|
|
|
|
Вопрос №1. Дать определение понятию «Формальная система»
Формальные система (ФС)- представляет собой совокупность чисто абстрактных объектов не связанных с внешним миром, в которой представлены правила оперирования множеством символов только в синтаксической трактовке, без учета смыслового содержания.
Вопрос №2. В каком порядке осуществляется формирование формальной теории
Формирование ФТ (теории) осуществляется в следующем порядке:
1. Задается конечное множество символов (алфавит).
2. Устанавливаются процедуры построения формул.
3. Устанавливается множество аксиом, то есть формул, которые истинны
ФТ-называют исчислением, под исчислением понимают формальное представление теории, которая позволяет оперировать с объектами без учета формального смысла выражений.
Вопрос №3. Понятие формулы ИВ
Это ФС интерпретацией которой является алгебра высказываний
Основной задачей ИВ является порождение обще логических законов – это тождественно истинных высказываний
Применительно к алгебре высказываний аксиоматический подход состоит в следующем:
1. Из всех формул алгебры высказываний выделяется некоторая часть, и они объявляются аксиомами
2. определяется некоторое правило, по которому из одних формул можно получить другие
3. правила выделяются так, что из аксиом могут быть получены все тавтологии алгебры высказываний.
Вопрос №4. Понятие доказуемой формулы
1. Всякая аксиома является доказуемой
2. Формула, получаемая из доказуемой формулы путем применения подстановки, есть доказуемая формула
3. Формула В, получаемая из доказуемых формул А и А->В путем применения правила заключения есть доказуемая формула
|
|
|
Правило подстановки – если формула А доказуемая, x – переменная, В – произвольная формула ИВ, то формула, полученная в результате замены в формуле А переменной х всюду, где находится формула В является также доказуемой формулой.
Уточнение правила:
-если формула А есть переменная х, то подстановка
даёт формулу В
-если А переменная у, то подстановка дает формулу А
-если А формула для которой уже определена, то подстановка В вместо х в отрицание А есть отрицание подстановки.
-если А1 и А2 формулы для которых подстановки уже определены, то подстановка
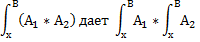
|- А (доказуема А)
Правила подстановки-> 
если формула А доказуема то доказуема и
Правила исключения
Если формулы А и А->В доказуемы, то формула В тоже доказуема.
Вопрос №5. Производные правила вывода.
Получаются с помощью правил подстановки и заключения и позволяют получить новые доказуемые формулы
1) Правило одновременной подстановки
Пусть А доказуемая формула, x1,x2, …xn переменные B1..Bn любые формулы исчисления высказывания. Тогда результат одновременной подстановки в А вместо x1,x2, …xn соответственно формуло1 B1..Bn доказуемой формулой.
2) Правило сложного заключения
Применимо к формулам следующего вида:
(*)
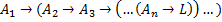И формулируется так:
Если формулы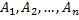 
и (*) доказуемы, то и формула L доказуема.
3) Правило силлогизма
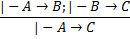
4) Правило контрапозиции
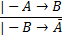
5) Правило снятия двойного отрицания
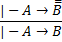
Вопрос №6. Понятие выводимости формул из совокупности формул
Будем рассматривать конечную совокупность формул H={A1,A2,…,An}
Определение формулы выводимой из совокупности H
1) Всякая формула Aj ϵ H является формулой, выводимой из H;
2) Всякая доказуемая формула выводима из H;
3) Если формулы С, С->B выводимы из H, то В также выводима из H;
Вопрос №7. Понятие вывода.
Выводом из конечной совокупности формул Н называется всякая конечная последовательность формул В1,В2,..Вn, всякий член которой удовлетворяет одному из условий:
|
|
|
1. Он является одной из формул совокупности Н
2. ОН является доказуемой формулой
3. Он получается по правилу заключения из двух любых предыдущих членов последовательности B1.B2...Bn
Вопрос №8. Правило выводимости.
Пусть H и W – это 2 совокупности формул ИВ. Будем понимать, что идет объединение этих множеств.
I. 
II.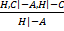 
III.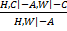 
IV.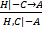 
V. Теорема дедукции
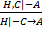
Обобщение теоремы дедукции:
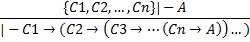
VI. Правило выделения конъюнкции: 
VII. Правило выделения дизъюнкции: 
VIII. Правило соединения посылок: 
IX. Правило разъединения посылок: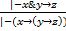 
|
|
|
