 |
Аналитический расчет времени замерзания жидкости при полной остановки движения в трубопроводе холодного водоснабжения расположенного на открытом воздухе при отрицательных температурах.
|
|
|
|
Расчет критической длины трубопровода.
Расчет падения температуры протекающей жидкости в трубопроводе. (частный случай – теплоизолированный трубопровод холодного водоснабжения расположенный на открытом воздухе) Определяем граничные условия: если А ≥ 2, то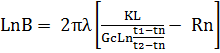 
; если А < 2, то 
, где А= 
; tср= 
B = D/d - отношение наружного диаметра изоляционного слоя к наружному диаметру изолируемо го объекта. λ - коэффициент теплопроводности изделия (Вт/мК) – определяется лабораторными испытаниями. К – коэффициент дополнительных потерь, учитывающий теплопотери через теплопроводные вклю чения в теплоизоляционных конструкциях, обусловленных наличием в них крепежных деталей и опор (т.№1 СНиП 41-103-2003): для Dy < 150мм. – 1,2; для Dy ≥ 150мм. – 1,15. L – длина трубопровода, м.; Rн - линейное термическое сопротивление наружной изоляционной конструкции (м2°С/Вт.). G – расход жидкости, кг./час; с – удельная теплоемкость жидкости, кDж / кг.°С. Проверяем граничные условия: 
, то , для упрочнения расчета значением 
пренебрегаем, и после преобразований получаем формулу для определения критической длины трубопровода: 
, с учетом постоянных значений получаем: для Dy < 150мм. Lкр = 0,705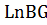 
, М = 0,705 
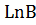; для Dy ≥ 150мм. Lкр = 0,736 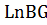, М = 0,736 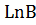, Lкр = MG (см. табл.№1, приложение №2)
Аналитический расчет времени замерзания жидкости при полной остановки движения в трубопроводе холодного водоснабжения расположенного на открытом воздухе при отрицательных температурах.
Определение времени полного замораживания жидкости в трубопроводе. Для нахождения времени полного замораживания жидкости в трубопроводе необходимо составить уравнение теплового баланса для однослойной цилиндрической изоляции и баланса охлаждающей во ды, а затем для баланса замерзающей воды: а) баланс для охлаждающей воды: 
dƮ = 
; после интегрирования уравнения по параметру времени, получаем выражение для нахождения време ни охлаждения жидкости от начальной температуры до температуры замерзания: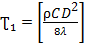 
LnB 
Ln 
. б) баланс для замерзающей воды: 
dƮ = 
, после интегрирования по времени, получаем: 
LnB. Суммарное время охлаждения воды до 0°С и ее полное замерзание определяется, как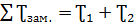 
, или после преобразований и использования постоянных величин - 
, где 
– переменный коэффициент, зависящий от расчетной температуры наружного воздуха, (см. табл.№2, приложение №2). 
– переменный коэффициент, зависящий от диаметра трубопровода и толщины теплоизо ляционного слоя, (см. табл.№4, приложение №2)
|
|
|
Определение напряжения в стенке трубопровода при замерзании в нем всего объема воды.
Объем всей замерзшей воды в трубопроводе с учетом коэффициента объемного расширения при изменении агрегатного состояния превращения воды в лед β 
составляет 
, или с учетом дополнительного объема, возникающего в следствии возникающего объемного расши рения: 
, В этом случае диаметр трубопровода увеличился бы и составил D1 , тогда 
или 
, а относительное удлинение периметра трубы составит: 
, или 
- из которого относительная деформация определяется в виде: 
, и с учетом численного значения коэффициента объемного расширения воды в лед при 0°С дает величину: 
Тогда напряжение в стенке стальной трубы согласно закону Гука составило бы: 
, что намного больше допускаемых напряжений для стальных труб 
. Необходимо найти долю 
замерзшей в трубопроводе воды, при которой напряжения начинают пре вышать допустимые. Тогда уравнение для доли объема замерзшей воды в трубопроводе запишется в виде: 
, а относительное удлинение периметра трубы: 
, или 
, то есть уже при 1,3% воды, превращаемой в лед, напряжения в стальной стенке трубопровода становится равным допустимому напряжению. где 
определяем согласно закону Гука: 
Уравнение теплового баланса для доли 
замерзшей воды в трубопроводе запишется в виде 
, а уравнение для времени замерзания доли 
воды в трубопроводе будет иметь вид: 
, а суммарное время охлаждения воды до 0°С и ее частичное замерзание, при котором напряжения в стенках трубы становятся равными допустимым и препятствует разрушению стенок трубопровода в следствии объемного расширения при замерзании воды в трубопроводе, определяется, как: 
LnB, (час.). После преобразований получаем выражение: 
, где 
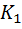– переменный коэффициент, зависящий от расчетной температуры наружного воздуха (см. табл.№3, приложение №2). – переменный коэффициент, зависящий от диаметра трубопровода и толщины теплоизоля ционного слоя, (см. табл.№4, приложение №2).
|
|
|
Приложения.
Приложение №1
Приложение №2
Коэффициенты для определения критической длины трубопровода и минимального расхода жидкости в трубопроводе.
Таблица №1
| Диаметр изолируемого трубопровода (мм.) | Толщина изоляции 𝛅 (мм.) |
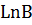
| М | Диаметр изолируемого трубопровода (мм.) | Толщина изоляции 𝛅 (мм.) |
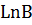
| М |
| 1,1999 | 1,41 | 0,5316 | 0,38 | ||||
| 1,3137 | 0,93 | 0,4228 | 0,30 | ||||
| 1,4633 | 1,03 | 0,4709 | 0,33 | ||||
| 1,17 | 0,82 | 0,4076 | 0,30 | ||||
| 1,2368 | 0,87 | 0,3895 | 0,29 | ||||
| 1,3863 | 0,98 | 0,3114 | 0,23 | ||||
| 1,0669 | 0,79 | 0,257 | 0,19 | ||||
| 0,98738 | 0,84 | 0,2849 | 0,21 | ||||
| 0,8473 | 0,60 | 0,2201 | 0,16 | ||||
| 0,8109 | 0,57 | 0,2445 | 0,18 | ||||
| 0,7191 | 0,51 | 0,2683 | 0,20 | ||||
| 0,8011 | 0,57 | 0,2141 | 0,16 | ||||
| 0,8769 | 0,62 | 0,2109 | 0,16 | ||||
| 0,5819 | 0,41 | 0,1728 | 0,13 | ||||
| 0,6529 | 0,46 | 0,1473 | 0,11 | ||||
| 0,7191 | 0,51 | 0,1301 | 0,096 | ||||
| 0,5153 | 0,36 | 0,1422 | 0,10 | ||||
| 0,5803 | 0,41 | 0,1151 | 0,085 | ||||
| 0,6413 | 0,46 | 0,1259 | 0,093 | ||||
| 0,50 | 0,36 | 0,1112 | 0,082 | ||||
| 0,554 | 0,39 | 0,0938 | 0,069 | ||||
| 0,4787 | 0,34 |
Коэффициент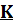 
. Таблица №2
| Расчетная температура наружного воздуха, °С | |||||
| -10 | -15 | -20 | -25 | -33 | |
| 48346,6 | 32301,3 | 24255,2 | 19419,1 | 14722,9 |
Коэффициент 
. Таблица №3
| Расчетная температура наружного воздуха, °С | |||||
| -10 | -15 | -20 | -25 | -33 | |
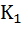
| 1809,7 | 1776,7 | 1361,8 | 1104,5 | 848,1 |
|
|
|
Таблица значений 
. Таблица №4
| Диаметр изолируемого трубопровода (мм.) | Толщина изоляции 𝛅 (мм.) |
| 
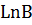
| Диаметр изолируемого трубопровода (мм.) | Толщина изоляции 𝛅 (мм.) |
|
|
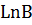
| 1,1999 | 0,00031 | 0,5316 | 0,006 | ||||
| 1,3137 | 0,00037 | 0,4228 | 0,0066 | ||||
| 1,4633 | 0,00038 | 0,4709 | 0,0074 | ||||
| 1,17 | 0,00057 | 0,4076 | 0,0092 | ||||
| 1,2368 | 0,00060 | 0,3895 | 0,0098 | ||||
| 1,3863 | 0,00067 | 0,3114 | 0,0125 | ||||
| 1,0669 | 0,00073 | 0,257 | 0,016 | ||||
| 0,98738 | 0,001 | 0,2849 | 0,0178 | ||||
| 0,8473 | 0,0014 | 0,2201 | 0,0198 | ||||
| 0,8109 | 0,0015 | 0,2445 | 0,022 | ||||
| 0,7191 | 0,0018 | 0,2683 | 0,0242 | ||||
| 0,8011 | 0,002 | 0,2141 | 0,0263 | ||||
| 0,8769 | 0,0022 | 0,2109 | 0,0338 | ||||
| 0,5819 | 0,00246 | 0,1728 | 0,0432 | ||||
| 0,6529 | 0,00276 | 0,1473 | 0,053 | ||||
| 0,7191 | 0,0031 | 0,1301 | 0,0638 | ||||
| 0,5153 | 0,0033 | 0,1422 | 0,0697 | ||||
| 0,5803 | 0,00371 | 0,1151 | 0,0737 | ||||
| 0,6413 | 0,0041 | 0,1259 | 0,0806 | ||||
| 0,50 | 0,005 | 0,1112 | 0,1112 | ||||
| 0,554 | 0,00554 | 0,0938 | 0,1126 | ||||
| 0,4787 | 0,00538 |
Приложение №3
Определение времени замерзания воды в трубопроводе 
, когда напряжения в стенках трубы, возникшие в следствии объемного расширения при изменении агрегатного состояния превращения воды в лед будут равными допустимым напряжениям – исключающее разрушение трубопровода, при различных значениях расчетной наружной температуры окружающей среды (час.). 
Таблица №5
| Диаметр изолируемого трубопровода (мм.) | Толщина изоляции 𝛅 (мм.) | Расчетная температура окружающего воздуха,  , 
| ||||
| - 10 | - 15 | -20 | -25 | - 33 | ||
| 0,6 | 0,6 | 0,4 | 0,4 | 0,3 | ||
| 0,7 | 0,7 | 0,5 | 0,4 | 0,3 | ||
| 0,7 | 0,7 | 0,5 | 0,4 | 0,3 | ||
| 1,1 | 1,0 | 0,8 | 0,6 | 0,5 | ||
| 1,1 | 1,1 | 0,8 | 0,7 | 0,5 | ||
| 1,2 | 1,2 | 0,9 | 0,7 | 0,6 | ||
| 1,4 | 1,3 | 1,0 | 0,8 | 0,6 | ||
| 1,8 | 1,8 | 1,4 | 1,1 | 0,8 | ||
| 2,6 | 2,5 | 1,9 | 1,5 | 1,2 | ||
| 2,7 | 2,7 | 2,1 | 1,7 | 1,3 | ||
| 3,3 | 3,2 | 2,5 | 2,0 | 1,5 | ||
| 3,6 | 3,6 | 2,8 | 2,4 | 1,7 | ||
| 4,0 | 3,9 | 3,0 | 2,4 | 1,9 | ||
| 4,5 | 4,4 | 3,4 | 2,7 | 2,1 | ||
| 5,0 | 4,9 | 3,8 | 3,1 | 2,3 | ||
| 5,6 | 5,5 | 4,3 | 3,4 | 2,6 | ||
| 6,0 | 5,9 | 4,5 | 3,6 | 2,8 | ||
| 6,7 | 6,6 | 5,1 | 4,1 | 3,1 | ||
| 7,5 | 7,3 | 5,6 | 4,5 | 3,5 | ||
| 9,1 | 8,9 | 6,8 | 5,5 | 4,3 | ||
| 10,0 | 9,9 | 7,6 | 6,1 | 4,7 | ||
| 9,8 | 9,6 | 7,4 | 5,9 | 4,6 | ||
| 10,9 | 10,7 | 8,2 | 6,6 | 5,1 | ||
| 11,9 | 11,8 | 9,0 | 7,3 | 5,6 | ||
| 13,4 | 13,2 | 10,1 | 8,2 | 6,3 | ||
| 16,7 | 16,4 | 12,6 | 10,2 | 7,8 | ||
| 16,9 | 16,6 | 12,8 | 10,8 | 8,3 | ||
| 22,7 | 22,2 | 17,1 | 13,8 | 10,6 | ||
| 29,0 | 28,5 | 21,8 | 17,7 | 13,6 | ||
| 32,3 | 31,7 | 24,3 | 19,7 | 15,1 | ||
| 35,9 | 35,2 | 27,0 | 21,9 | 16,8 | ||
| 39,9 | 39,1 | 30,0 | 24,3 | 18,7 | ||
| 43,8 | 43,0 | 33,0 | 26,7 | 20,5 | ||
| 47,6 | 46,8 | 35,9 | 29,1 | 22,3 | ||
| 61,2 | 60,1 | 46,1 | 37,3 | 28,7 | ||
| 78,2 | 76,8 | 58,9 | 47,7 | 36,6 | ||
| 96,0 | 94,2 | 72,2 | 58,5 | 44,9 | ||
| 115,5 | 113,4 | 86,9 | 70,5 | 54,1 | ||
| 126,1 | 123,9 | 94,9 | 77,0 | 59,1 | ||
| 133,4 | 131,0 | 100,4 | 81,4 | 62,5 | ||
| 145,9 | 143,2 | 109,8 | 89,0 | 68,4 | ||
| 201,3 | 197,6 | 151,4 | 122,8 | 94,3 | ||
| 203,8 | 200,1 | 153,4 | 124,4 | 95,5 |
|
|
|
Список литературы: 1. СП 41-103-2003 – Проектирование тепловой изоляции трубопроводов и оборудования. 2. СНиП 41-03-2003 – Тепловая изоляция оборудования и трубопроводов. 3. СНиП 23-01-99 – Строительная климатология. 4. Приложение №1 - Показатели лабораторных испытаний теплоизоляционных изделий. 5. ГОСТ 14249-89 - Сосуды и аппараты. Нормы расчета на прочность. 6. Шавлов А.В. – Лед при структурных превращениях, Наука, 1996.- 362с. 7.. А.Б. Дулькин, А.Б.Голованчиков – Оценка времени замерзания воды в трубопроводе. ДК 621.64
|
|
|
