 |
Логарифмическое дифференцирование
|
|
|
|
Если требуется найти  из уравнения
из уравнения 
 , то можно:
, то можно:
а) логарифмировать обе части уравнения 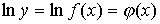 ;
;
б) дифференцировать обе части полученного равенства, где  есть сложная функция от х,
есть сложная функция от х, 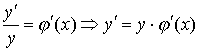 .
.
в) заменить 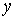 его выражением через х
его выражением через х  .
.
Пример: 

§6. Метод логарифмического дифференцирования. 
5. Дифференцирование неявных функций Пусть уравнение  определяет
определяет 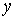 как неявную функцию от х. а) продифференцируем по х обе части уравнения
как неявную функцию от х. а) продифференцируем по х обе части уравнения  , получим уравнение первой степени относительно
, получим уравнение первой степени относительно  ; б) из полученного уравнения выразим
; б) из полученного уравнения выразим  .
.
Пример:  .
. 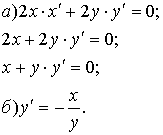
В21.Приращение и дифференциал функции одной переменной.Условия существования диффренциала. Инвариантность форм записи дифференциала первого порядка.
Дифференциал функции:
Пусть функция y=f(x) дифференцируема в точке х: т.е. для её приращения Dу в этой точке выполняется равенство [2]. Тогда Dу есть сумма двух слагаемых. Первое из них A Dx пропорционально Dx, а в таких случаях говорят, что оно есть линейная однородная функция от Dх. Второе – о (Dх)Dx®0 является бесконечно малой функцией высшего порядка малости сравнительно с Dx. Если А¹0, то второе слагаемое стремится к нулю при Dx®0 быстрее, чем первое. В связи с этим первое слагаемое A Dx=f'(x)Dx наз. главным членом приращения Dy. Это слагаемое называют дифференциалом функции и обозначают символом dy. Итак, по определению dy=df=f'(x)Dx. На (рис. 47) изображен график Г функции y=f(x);
 Т –касательная к Г в точке A, имеющей абсциссу х; f'(x)=tga, где a – угол, образованный касательной с осью х; dy=f'(х)Dx=tgaDx=CD, DB=Dy–dy= o (Dx)Dx®0. Таким образом, дифференциал функции у в точке х, соответствующий приращению Dx, есть приращение ординаты точки, лежащей на касательной (dy=CD). Вообще говоря, dy¹Dy, ибо Dy=dy+ o (Dx)Dx®0, а второй член этой суммы, вообще говоря, не равен нулю. Только для линейной функции у=Ах+В имеет место равенство Dу=А Dx=dy для любого х. В частности, для у=х, dy=dx=Dx т.е. дифференциал и приращение независимой переменной равны между собой (dx=Dx). Поэтому дифференциал произвольной функции f обычно записывают так: dy=f'(x)dx, откуда f'(x)=dy/dx,
Т –касательная к Г в точке A, имеющей абсциссу х; f'(x)=tga, где a – угол, образованный касательной с осью х; dy=f'(х)Dx=tgaDx=CD, DB=Dy–dy= o (Dx)Dx®0. Таким образом, дифференциал функции у в точке х, соответствующий приращению Dx, есть приращение ординаты точки, лежащей на касательной (dy=CD). Вообще говоря, dy¹Dy, ибо Dy=dy+ o (Dx)Dx®0, а второй член этой суммы, вообще говоря, не равен нулю. Только для линейной функции у=Ах+В имеет место равенство Dу=А Dx=dy для любого х. В частности, для у=х, dy=dx=Dx т.е. дифференциал и приращение независимой переменной равны между собой (dx=Dx). Поэтому дифференциал произвольной функции f обычно записывают так: dy=f'(x)dx, откуда f'(x)=dy/dx,
|
|
|
т.е. производная функции f в точке х равна отношению дифференциала функции в этой точке к дифференциалу независимой переменной х.
Это объясняет, что выражение dy/dx употребляется как символ для обозначения производной. Надо иметь в виду, что дифференциал dx независимой переменной не зависит от х, он равен Dx – произвольному приращению аргумента х. Что же касается дифференциала dy функции у (отличной от х), то он зависит от х и dx. Отметим формулы:
d(u±u¹)=du±du [3]; d(u×u)=udu+udu [4]; d(cu)=cdu (c – постоянная) [5]; d(u/u)=(udu–udu)/u2 (при u¹0) [6]; где предполагается, что u и u – дифференцируемые функции в рассматриваемой точке х. Например, формула [6] доказывается так:

Определение: Пусть y=f(x) определена в некоторой О(х0) – она называется дифференцируемой в точке х0, если её приращение в этой точки представимо в виде:
∆y=∆f(x0)=A∆x+a(∆x)∆x)1
a(0)=0 A=const
Определение: линейная ∆х часть приращение дифференцируемой функции называется дифференциалом функции в точке х0:
dy=df(x0)ºA∆x
Теорема: Если функция дифференцируема в точке х0 то A=f’(x0), то она имеет производную в этой точке, то A=f’(x0); наоборот если функция имеет производную в этой точке, то она дифференцируема в этой точке – называется дифференциалом.
Доказательство:Пусть y=f(x) дифференцируема в точке х0, то есть в некоторой О(х0) справедливо равенство ∆f(x0)=A∆x+a(∆x)∆x1; a(0)=0. Поделим обе части этого равенства на ∆х и приведём к пределу при ∆х®0:
lim(∆f(x0))/∆x=lim(A+a(x))=A. Этот предел существует, меньше ¥, тогда по определению этот предел есть
∆x®0 ∆x®0
|
|
|
производная.
Доказательство: (в обратную сторону) Пусть в точке х0 $ f’(x0)(<¥) – это означает, что f(x) определена в некоторой О(х0) и $ lim(∆f(x0))/∆x=f’(x0)Þ по определению предела следует, что в некоторой О(х0)
∆x®0
(∆f(x0))/∆x=a(∆х)+f’(x0) при ∆х®0 Þ ∆f(x0)=f’(x0)+a(∆x)∆x, так как lima(∆x)=0, то в точке х0 y a(∆x) может
∆х®0
быть лишь устранимым разрывом. Устраним его, определим и доопределим:
a(0)=0, тогда ∆f(x0)=f’(x0)∆x+a(∆x)∆x Þ A=f’(x0) из установленного соответствия получим выражения для дифференцируемой функции df(x0)=f’(x0)∆x
Следствие: по определению полагают дифференциал независимой переменной равной её приращению
dx=∆x (х - независимая переменная)
df(x)=f’(x)dx
f(x)=x – вычислим дифференциал f’(x)=1 df(x)=dx=f(x)∆x=1∆x
Замечание: дифференциал функции зависит от двух переменных – от самой точки х и от ей приращения
y=cosx x0=p/2 ∆x=p/180
y’=-sinx y’(p/2)=-sin(p/2)=-1
dy(p/2)=-1∆x=-1p/180=-p/180
Теорема: Пусть y=f(x) дифференцируема в точке х0, а z=g(y) дифференцируема в точке у0=f(x0), тогда сложная функция z=g(f(x) - дифференцируема в точке х0 и z’(x0)=g’(f)f’(x)
Доказательство: (1) ∆z=g’(y0)∆y+a(∆y)∆y
(2) ∆y=f(x0)∆x+b(∆x)∆x a(0)=0 b(0)=0
Подставим в первое равенство второе:
∆z=g’(y0)f(x0)∆x+g’(y0)b(∆x)∆x+a[f’(x0)+b(∆x)∆x][f’(x0)∆x+b(∆x0∆x]
lim∆z/∆x=limg’(x0)f’(x0)+limg’(x0)b(∆x)+lim a(f’(x0)+b(∆x)∆x)[f’(x0)+b∆x] Þ z’(x0)=g’(y0)f’(x0) что и требовалось
∆x®0 ∆x®0 ∆x®0 ∆x®0
доказать.Св-ва:
1. (U±V)`=U`±V`, то (U±V)`dx=U`dx±V`dx, d(U±V)=d(U±V)
2. (UV)`=U`V+V`U, то (UV)`dx=V`dU+U`dV
3.d(c)=c`dx=0*dx=0
4. d(U/V)`=(V`dU-U`dV)/V2.
Инвариантность форм записи: дифференциал сложной функции имеет тот же вид, какой он имел бы в том случае, если бы промежуточный аргумент и был независимой переменной. Иначе:форма дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. Найдем диф.сложной функции: y=f(u), u=g(x) или y=(f(g(x))). По правило диффер.сложной функции: dy/dx=f’(u)g’(x) => dy=f’(u)g’(x)dx но g’(x)dx=du поэтому dy=f’(u)du
В22.Геометрический смысл дифференциала функции одной перменной. Касательная и нормаль к плоскости.
Геометрический смысл дифференциала функции и уравнение касательной.

 |
f’(x0)=tga
уравнение прямой: Y=kx+b
y0=f(x0)=kx0+b
k-угловой коэффициент прямой
|
|
|
k=tga=f’(x0)
Y=f(x0)+f(x0)-f’(x0)x0
b=f(x0)-kx0
Y=f(x)+f’(x0)(x-x0)
∆f(x0)=f’(x0)∆x+a(∆x)∆x при ∆х®0 Þ в некоторой
O(x0) f(x0)=f’(x0)+f’(x0)∆x+a(∆x)∆x при ∆х®0
Y1=f(x0)+f’(x0)(x-x0)a=f’(x0)+f’(x0)∆x
df(x0)=f’(x0)∆x
Геометрический смысл дифференциала:
df(x0) – это приращение ординаты при движение по касательной проведённой к графику функции в точки (х0;f(x0).
Замечание: Часто говорят о касательной проведённой в точке х0.
Линеаризация функции.
Определение: Замена функции в окрестности данной точки линейной функции называется линеаризацией функции, точнее в О(х0) заменяется отрезком касательной в точке х0.
 (*) f(x)-Y=a(∆x)∆x-o(∆x)
(*) f(x)-Y=a(∆x)∆x-o(∆x)
Если в равенстве (*) отбросить правую часть, то мы
получим приближённое равенство:
f(x)»f(x0)+f’(x0)(x-x0), x»x0
Y=f(x0)+f’(x0)(x-x0) – уравнение касательной в точке х0
Формула получена из определения дифференциала в точке х0 функции
f(x)=f(x0)+f(x0)∆x+o∆x при ∆х®0 – называется критерием дифференциальности функции в точке х0.
Рассмотрим кривую, уравнение которой есть y=f(x). Возьмем на этой кривой точку М(х  , у
, у  ), и составим уравнение касательной к данной кривой в точке М, предполагая, что эта касательная не параллельна оси Оу.
), и составим уравнение касательной к данной кривой в точке М, предполагая, что эта касательная не параллельна оси Оу.
Уравнение прямой с угловым коэффициентом в общем виде есть у=kх + b. Поскольку для касательной k=f ¢(x  ), то получаем уравнение y=f ¢(x
), то получаем уравнение y=f ¢(x  )×x + b. Параметр b найдем из условия, что касательная проходит через точку М(х
)×x + b. Параметр b найдем из условия, что касательная проходит через точку М(х  ,
,  ). Поэтому ее координаты должны удовлетворять уравнению касательной: у
). Поэтому ее координаты должны удовлетворять уравнению касательной: у  = f ¢(x
= f ¢(x  )×x
)×x  + b. Отсюда b=y
+ b. Отсюда b=y  – f ¢(x
– f ¢(x  )×x
)×x  .
.
Таким образом, получаем уравнение касательной y=f ¢(x  )×x +y
)×x +y  - f ¢(x
- f ¢(x  )×x
)×x  или
или
y = f ¢(x  )×(x – x )×(x – x  ) + f(x ) + f(x 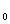 ) )
|
Если касательная, проходящая через точку М(х  ,
,  ) параллельна оси ординат (т.е. производная в этой точке не существует), то ее уравнение х=х
) параллельна оси ординат (т.е. производная в этой точке не существует), то ее уравнение х=х  .
.
 Наряду с касательной к кривой в данной точке часто приходится рассматривать нормаль.
Наряду с касательной к кривой в данной точке часто приходится рассматривать нормаль.
Нормалью к кривой в данной точке называется прямая, проходящая через эту точку перпендикулярно к касательной в данной точке.
Из определения нормали следует, что ее угловой коэффициент 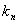 связан с угловым коэффициентом касательной к равенством:
связан с угловым коэффициентом касательной к равенством:
|
|
|
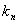 = tg b = tg(90° + a) = - ctg a =
= tg b = tg(90° + a) = - ctg a =  =
=  =
=  .
.
Учитывая, что нормаль также как и касательная проходит через точку М(х  , у
, у  ), то уравнение нормали к кривой y=f(x) в данной точке М имеет вид:
), то уравнение нормали к кривой y=f(x) в данной точке М имеет вид:
y = 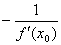 ×(x – x ×(x – x  )+f(x0) )+f(x0)
|
Ясно, что если касательная параллельна оси Ох, т.е. f ¢(x  )=0 и ее уравнение имеет вид у=у
)=0 и ее уравнение имеет вид у=у  , то нормаль в этой же точке будет перпендикулярна оси Ох. Значит, ее уравнение имеет вид х=х
, то нормаль в этой же точке будет перпендикулярна оси Ох. Значит, ее уравнение имеет вид х=х  .
.
В23.Производные и дифференциалы порядка выше первого функции одной переменной. Нарушение инвариантности форм записи. Линейная замена переменной. Производные функции, заданной параметрически.
Существует f’(x) " xÎ(a,b), тогда эта производная сама является функцией х g(х)=f’(x) и можно ставить о дифференцируемости этой функции.
Существует g’(x) " xÎ(a,b), то мы называем её второй производной g’(x)ºf’’(x)

Диф.высших порядков не инвариантен: d2 y=d(F’(u)du) Но здесь du=g’(x)dx зависит от х и поетому мы получаем d2y=d(F(u))du+F’(u)d(du) или d2y=F’’(u)(du)2+F’(u)d2u где d2u=g’’(x)(dx)2
Дифференцирование функций, заданных параметрически
Пусть функция задана параметрическими уравнениями  ,тогда
,тогда  , или
, или  риме:
риме: 
В24.Точка монотонности функции и достаточное условие их существования.Точки экстремума функции.Необходимое условие экстремума функции..
Если x2>x1, f(x2)>f(x1), то ф-ция монотонно возрастает
Если x2>x1, f(x2)<f(x1), то ф-ция монотонно убывает
Монотонность - постоянство
Необходимые признаки:1)если ф-ция f(x) всюду в интервале возрастает, то ее производная в этом интервале неотрицательна (f`(x)>=0)
2)если ф-ция f(x) всюду в интервале убывает, то ее производная в этом интервале неположительная (f`(x)<=0)
3)если ф-ция f(x) всюду в интервале постоянна, то ее производная в этом интервале =0 (f`(x)=0)
Достаточные признаки монотонности: 1)если f`(x) в интервале положительна, то ф-ция f(x) возрастает в этом интервале.
2)если f`(x)<0, то ф-ция f(x) возрастает в этом интервале.
3)если f`(x)=0, то ф-ция f(x)=const на интервале.
x1<a<x2, x2-x1>0, x2>x1
1. если f`(a)>0, то f(x2)>f(x1)
2. если f`(a)<0, то f(x2)<f(x1)
3. если f`(a)=0, то f(x2)=f(x1)
Точка х называется точкой max ф-ции, если значение ф-ции в этой точке - наименьшее в некоторой ее окрестности.
1- локальный max
2- локальный min
3- глобальный max
4- глобальный min
если tga>0, то f`(x)>0
если tga<0, то f`(x)<0
Необходимый признак экстремума: ф-ия f(x) может иметь max и min только в тех точках, в которых f`(x)=0 или не существует.
 (В них можно построить ¥ касательных).
(В них можно построить ¥ касательных).
Достаточный признак: точка х0 является точкой экстремума, если ее производная в этой точке меняет знак:
- если с “+” на “-”, то х0- т. max
- если с “-” на “+”, то х0- т. min


В25 Теорема Роля и ее геометрический смысл.
|
|
|
Теорема (Ролля):
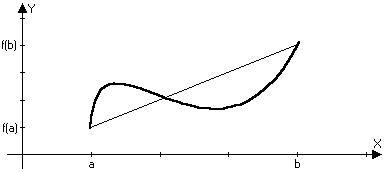
Пусть функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема на (a,b). Кроме того на концах интервала она принемает равные значения f(a)=f(b), тогда $ сÎ(a,b): f(c)=0
Доказательство: Така как функция непрерывна на отрезке [a,b], то по второй теореме Вейштрасса есть наибольшее и наименьшее значение (m,M), если m=M, то f(x)ºconst ("xÎ[a,b]) (const)’=0.
Пусть m<M, тогда либо m, либо М отлична от значений на концах отрезка. Пусть например M¹f(a):$ c(a,b):f(c)=M, то есть точка с точка экстремума максимума следовательно по теореме Ферма f’(c)=0
Замечание: условие дифференцируемсти нельзя отбросить.

непрерывна на отрезке [a,b]
Геометрический смысл.

f’(x)=0, то касательная || оси х. Теорема не утверждает, что это единственная точка.

В26.ТеоремаЛангранжа и Коши о диф.на отрезках функциях.
Теорема Лангранджа:
Пусть функция y=f(x) непрерывна на отрезке [a,b] и дифференцируема на отрезке (а,b), то $ сÎ(a,b): f(b)-f(a)=f(c)(b-a)
Доказательство:
F(x)=f(x)+lx где l - пока неизвестное число.
F(x) – непрерывна на отрезке [a,b] как сумма непрерывной функции
f(x) – дифференцируема на отрезке [a,b] как сумма дифференцируемой функции.
Выберем число l, так чтобы на отрезке [a,b] F(x) принимало равное значение.
F(a)=f(a)+la
 F(b)=f(b)+lb
F(b)=f(b)+lb
F(a)=F(b) Þ f(a)-f(b)=l(a-b) Þ l=[f(b)-f(a)]/[b-a]
F(x) – удовлетворяет условию теоремы Роллера на отрезке [a,b] Þ $ cÎ(a,b):F’(c)=0, то есть F’(x)=f’(x)+l 0=f’(c)+l Þ f’(c)=-l=[f(b)-f(a)]/[b-a] То есть на кривой которая наклонена к оси х под таким же углом как и секущая [f(b)-f(a)]/[b-a]=tga=f(x) $ cÎ(a,b) Замечание: Часто точку с можно представить в
нужном виде: с=х0+q∆х 0<(c-x0)/(x-x0)= q<1 c-x0=q(x-x0) c=x0+q(x-x0)1 f(x)-f(x0)=f’(x0+q∆x)(x-x0) 0<q<1 ∆f(x0)=f’(x0+q∆x)∆x
Если f(x), g(x) удовл. трем условиям:
1). f(x), g(x) непрерыв. на промеж [a,b]
2). f(x), g(x) деффер. на интервале (a,b)
3). g’(x)¹0 на интер. (a,b), то сущ. т. с

: Отметим прежде всего, что g(b)¹g(a), так как по теореме Ролля для функции g(x)
F(x)=(f(x)-f(a)) (g(b)-g(a))-(f(b)-f(a))(g(x)-g(a)) –вспомогательная фун-я
Требуем:1.F(x) определена и непрерывна на всем [a;b]т.к. она линейная кобминация непрерывных.2.F(x) дифференцируема на всем промежутке т.к. коомб. 3. F(a)=0 F(b)=0
F(a)=F(b)=0 – все условия т.Ролля => внутри [a;b] есть С, где F’(C)=0 выразим это f’(x)(g(b))-g(a))-(f(b)-b(a))g’c=0
 Справедлива, тюк. g(b)!=g(a)по Ролю
Справедлива, тюк. g(b)!=g(a)по Ролю
В27.Правило Лопиталя.
Правила Лопиталя.
Это правило в случае дифференцируемости функции позволяет избавляться от неопределённостей типа 0/0 или ¥/¥ при вычисление пределов.
Теорема: Пусть функции f(x) и g(x) дифференцируемы в О(х0), g’(x0)¹0 в О°(х0), f(x0)=g(x0)=0 и $
lim f’(x)/g’(x)=k (конечный или бесконечный предел), тогда $ lim f(x)/g(x)=lim f’(x)/g’(x)=k
x®x° x®x° x®x°
Доказательство: lim f(x)/g(x)=lim [f(x)-f(x0)]/g(x)-g(x0)=lim f’(c(x))/g’(c(x))= | $ c=c(x) лежащая между х их0 если
x®x° x®x° x®x°
х®х0 то с®х0 | =lim f’(x)/g’(x)=k
x®x°
Замечание(1): f(x0)=g(x0)=0 требование можно заменить требованием lim f(x)=0, lim g(x)=0, то есть в т х0 f(x) и
x®x° x®x°
g(x) могут иметь устранимый разрыв, действительно достаточно переопределить или доопределить f(x) и g(x) по непрерывности, так чтобы f(x0)=g(x0)=0
Замечание(2): Если $ f’(x0) и g’(x0), g’(x0)¹0, то утверждение теоремы будет:
lim f(x)/g(x)=lim f’(x)/g’(x)=lim [(x-x0)(f’(x0)+a(x-x0))]/ [(x-x0)(g’(x0)+b (x-x0))]=f’(x0)/g’(x0)
x®x° x®x° x®x°
Теорема: (¥/¥) Пусть функции f(x) и g(x) непрерывны в О°(х0), g'(x)¹0 и О°(х0), дифференцируемы в О°(х0) и
lim f(x)=lim g(x)=¥; $ lim f’(x)/g’(x)=k. Тогда lim f(x)/g(x)=lim f’(x)/g’(x)=k
x®x° x®x° x®x° x®x° x®x°
Без доказательства!
Замечание: Если функции f’(x) и g’(x) сами удовлетворяют условия теоремы то правило Лопиталя можно применить повторно:
f(x)=ex g(x)=xn x®¥
lim ex/xn= lim ex/1!=¥ "nÎ N lim ex/xn= lim ex/nxn-1= lim ex/[n(n-1)xn-2]=lim ex/n!=+¥
 x®+¥ x®+¥ x®+¥ x®+¥ x®+¥ x®+¥
x®+¥ x®+¥ x®+¥ x®+¥ x®+¥ x®+¥
f(x)=lnx
x®+¥
g(x)=xn
lim lnx/xn= lim (1/x)/nxn-1= lim 1/nxn=0
x®+¥ x®+¥ x®+¥
В28.Формула Тейлора с остаточным членом в форме Лангранжа.
Пусть на интервале [a, b] функция f(x) дифференцируема n раз и выполняются следующие равенства:
f(a) = f(b) = f '(a) = f ''(a)=... = f (n-1)(a)=0
Тогда внутри интервала [a, b] найдется хотя бы одно значение с, при котором
f (n)(c) = 0
Доказательство. По теореме Ролля имеем
f '(x0) = 0,
где a < x0 < b. Тогда f '(x) на интервале [a, x0] удовлетворяет теореме Ролля, так как, по условию, f '(a) = 0 и f '(x0) = 0, а потому
f ''(x1) = 0,
где a < x1 < x0.
Применяя теорему Ролля последовательно к функциям f ''(x), f '''(x),..., f (n-1)(x), найдем наконец:
f (n)(с) = 0,
где a < c < xn-1 < b. Теорема доказана.
Выведем теперь формулу Тейлора с остаточным членом в форме Лагранжа.
Пусть функция f (x) дифференцируема n раз на интервале [a, b].
Рассмотрим вспомогательную функцию
j (x) = f (x) - P (x),
где

Продифференцируем n раз функцию j (x). Тогда будем иметь



............................
j (n-1)(x) = f(n-1)(x) - An-1 - An(x - a),
j (n)(x) = f(n)(x) - An
Потребуем, чтобы функция j (x) удовлетворяла условиям обобщенной теоремы Ролля. Тогда будем иметь
 (1)
(1)
 .
.
Так как функция j (x) удовлетворяет условиям обобщенной теоремы Ролля, то найдется такое значение с (a < c < b), что
j (n)(с) = f(n)(с) - An = 0 (2)
Далее найдем из n первых уравнений системы (1) коэффициенты A0, A1,..., An-1:
A0 = f(a), A1 = f'(a), A2 = f''(a),..., An-1 = f(n-1)(a),
а из уравнения (2) коэффициент An: An = f(n)(c) и подставим их значения в последнее уравнение системы (1):
 ,
,
где 0 < Q < 1
Заменяя b на x, получим формулу Тейлора:

где 0 < Q < 1
Последнее слагаемое

называется остаточным членом в форме Лагранжа.
При a = 0 получается так называемая формула Маклорена:
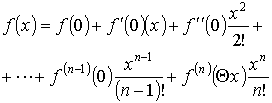
где 0 < Q < 1, а остаточный член записывается в виде

В29.Условие монотонности функции на промежутке. Условие постоянства функции на промежутке и его свойства.

Пусть f(x) определена и непрерывна на [a;b] и имеет конечную производную во всех точках.Для того, чтобы функ-я была постоянной достаточно чтобы производная=0 в каждой точке отрезка.
Док-во по теореме лангранжа есть хоть одно С из (x0,x) для которого f(c)=f(x0)+f’(c)(=0)(x-x0) (f’(x)-f(x))/(x’-x0)=f’(c) f(x)=f(x)
Следствие: f(x) и g(x) непрер, имеют производн и если производн совпад., то фун-и отличаются на постоянную величину.
Док-во: h(x)=f(x)-g(x) h’(x)=f’(x)-g’(x)=0 f-g=c f=g+c
В30.Достаточные признаки экстремума функции 1 переменной
Экстремумы функции.
 Можно указать О(х1) в которой все значения функции
Можно указать О(х1) в которой все значения функции
f(x)<f(x1) b и О°d1(х1) анологично для точки х2
f(x)>f(x1) b и О°d2(х1). Значенгие функции в точке М1, М3 и М5 –
max; M2 и М4 – min – такие точки назавыются точкками
экстремума или точками локального max и min.
Определение: (точки экстремума)
Пусть функия f(x) определена в некоторой О(х0) и f(x)>f(x0) в
О°(х0) или f(x)<f(x0) в этом случае точка х0 – называется точкой локального max (min).
 Замечание:
Замечание:
f(x)£f(x1) в Оd1(х1)
f(x)³f(x2) в Оd2(х2)
говорят, что точки х1 и х2 точки не строгого локального
экстремума.
Теорема: (Ферма) (о необходимости условия экстремума дифференцируемой функции)
Пусть y=f(x) дифференцируема в точки х0 и точка х0 – точка экстремума, тогда f(x0)=0
Доказательсто: Заметим, что х0 точка экстремума, то в её окрестности f(x) – f(x0) сохраняет знак. Запишем условие ∆f(x0)=f(x)-f(x0)(x-x0)+o(x-x0)
f(x)-f(x0)=(x-x0)[f(x0)+a(x-x0)] то при х – достаточно близких к х0 знак выражения стоящего в квадратных скобках совпадает со знаком f’(x0)¹0 (x-x0) – меняет знак при переходе черех точку х0 Þ f’(x0)=0
Функция u=f(Р) имеет максимум (минимум) в точке P0(x01,...,x0n), если существует такая окрестность точки P0, для всех точек Р (x1,...,xn)которой, отличных от точки P0, выполняется неравенство f(Р0)>f(Р) (соответственно f(Р0)<f(P)). Максимум или минимум функции наз. её экстремумом. Необходимое условие экстремума: Если дифференцируемая функция f(Р) достигает экстремума в точке P0, то в этой точке
f'xk(P0)=0 для всех k=1,2,...,n {1} или df(P0,Dx1,...,Dxn)=0 тождественно относительно,Dx1,...,Dxn. Точки, в которых выполняются условия {1} наз. стационарными точками функции u=f(Р). Таким образом, если P0 – точка экстремума функции u=f(P), то либо P0 – стационарная точка, либо в этой точке функция не дифференцируема. Достаточные условия экстремума. Пусть P0(x01,...,x0n) – стационарная точка функции u=f(P), причем эта функция дважды дифференцируема в некоторой окрестности точки P0 и все её вторые частные производные непрерывны в точке P0. Тогда: (1) если второй дифференциал d2u(P0(Dx1,...,Dxn)) как функция Dx1,...,Dxn имеет постоянный знак при всевозможных наборах значений Dx1,...,Dxn не равных одновременно нулю, то функция u=f(P) имеет в точке P0 экстремум, а именно – максимум при d2u(P0(Dx1,...,Dxn))<0 и минимум при d2u(P0(Dx1,...,Dxn))>0; (2) если d2u(P0(Dx1,...,Dxn)) является знакопеременной функцией Dx1,...,Dxn, т.е. принимает как положительные, так и отрицательные значения то точка P0 не является точкой экстремума функции u=f(P); (3) если d2u(P0(Dx1,...,Dxn))³0 или d2u(P0(Dx1,...,Dxn))£0, причем, существуют такие наборы значений Dx1,...,Dxn не равных одновременно нулю, для которых значение второго дифференциала обращается в нуль, то функция, u=f(P) в точке P0 может иметь экстремум, но может и не иметь его (в этом случае для выяснения вопроса требуется дополнительное исследование). В частном случае функции двух переменных достаточные условия экстремума можно сформулировать следующим образом. Пусть P0(x0,y0) – стационарная точка функции z=f(x,y) причем эта функция дважды дифференцируема в некоторой окрестности точки P0 и все её вторые частные производные непрерывны в точке P0. Введем обозначения: A=f''xx(x0,y0), B=f''xx(x0,y0), C=f''xx(x0,y0) D=AC–B2. Тогда: [1] если D>0, то функция z=f(х,у) имеет в точке Р0(x0,y0) экстремум, а именно – максимум при А<0 (С<0) и минимум при А>0 (С>0); [2] если D<0, то экстремум в точке Р0(x0,y0) отсутствует; [3] если D=0, то требуется дополнительное исследование.
В31.Вогнутость, выпуклость, точки перегиба графика функции. Условиях их существования


 Выпуклость и вогнутость.
Выпуклость и вогнутость.
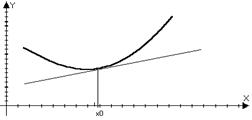
Определение: Пусть функция f(x) – дифференцируема в
точке х0, то она называется выпуклой (вогнутой) в верх
в точке х0, если f(x)-yкас<0 в О(х0)
 |
Определение: Пусть функция f(x) – дифференцируема в
точке х0, то она называется выпуклой (вогнутой) вниз в
точке х0, если f(x)-yкас>0 в О(х0)
Определение: Пусть функция f(x) – дифференцируема в
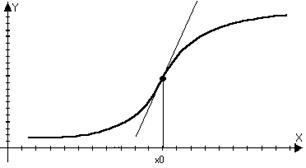 точке х0, то она называется выпуклой (вогнутой) в верх
точке х0, то она называется выпуклой (вогнутой) в верх
(вниз) на интервале (a,b), если она выпукла в верх (вниз)
в каждой точке этого интервала.
Определение: (точки перегиба) Пусть функция f(x) диф-
ференцируема в О°(х0) и непрерывна в О(х0). Точка х0 –
называется точкой перегиба графика f(x), если при пере-
ходе через точку меняется знак выпуклости.
Теорема: (о достаточном условие выпуклости функции).
Пусть функция f(x) дважды дифференцируема в точке х0 и f’’(x0)<0 (f’’(x0)>0), тогда f(x) – выпукла вверх (вниз) в тоске х0.
Доказательство: Напишем формулу Тейлора с остаточным членом в форме пеано:
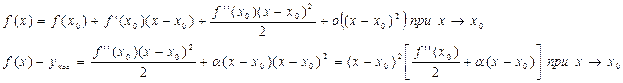
Если х близко к х0, то знак квадрата скобки определяется знаком f(x0). Если f’’(x0)<0, то f(x)-yкас>0 в О°(х0).
Если f’’(x0)>0, то f(x)-yкас>0 в О°(х0)
Теорема: Путь функция f(x) непрерывна в О(х0) и дважды дифференцируема в О°(х0), причём f’(x) меняет знак при переходе через точку х0, тогда точка х0 – точка перегиба.
Доказательство:
f’’(x) - +
 (·) x
(·) x
x0
f’’(x)<0 в O°-(x0)Þ f(x) – выпукла вверх в О°-(х0)
f’’(x)>0 в O°+(x0)Þ f(x) – выпукла вниз в О°+(х0)
Следствие: Если f(x) дважды дифференцируемы в точке х0. Если точке х0 точка перегиба, то f’’(x0)=0
Путь точка х0 точка перегиба и существует f’’(x0)>0, тогда

то есть при переходе через точку х0 левая часть равенства f(x)-yкас не меняет знак. Аналогично получаем для f(x)>0 f’’(x0)=0
Замечание: Условие равенства f’’(x0)=0 необходимо, но недостаточно.
В32.Вертикальные и наклонные асимптоты графика функции.
Асимптоты.
1. Вертикальные
1.1 Пусть функция f(x) определена в  , тогда прямая х=х0 называется правой вертикальной асимптотой для функции f(x)
, тогда прямая х=х0 называется правой вертикальной асимптотой для функции f(x) 
1.2  Пусть функция f(x) определена в
Пусть функция f(x) определена в  , тогда прямая х=х0 называется левой вертикальной асимптотой для функции f(x)
, тогда прямая х=х0 называется левой вертикальной асимптотой для функции f(x) 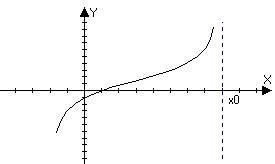

2. Наклонные асимптоты
2.1 Пусть функция f(x) определена в  , тогда прямая y=kx+b называется правой наклонной асимптотой для функции f(x). (Если k=0, то говорят, что y=b – горизонтальная асимптота).
, тогда прямая y=kx+b называется правой наклонной асимптотой для функции f(x). (Если k=0, то говорят, что y=b – горизонтальная асимптота). 

2.2 Пусть функция f(x) определена в 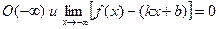 , тогда прямая y=kx+b называется левой наклонной асимптотой для функции f(x).
, тогда прямая y=kx+b называется левой наклонной асимптотой для функции f(x).


|
|
|


