Задачи для самостоятельного решения

 

1. Планируется деятельность четырех промышленных предприятий (системы) на очередной год. Начальные средства: S ₀=5 условных единиц. Размеры вложения в каждое предприятие кратны 1 условной единице. Средства Х, выделенные k –му предприятию (k =1, 2, 3, 4), приносит в конце года прибыль f_k (X). Функции f_k (X) заданы таблично:

Х	f 1(X)	f 2(X)	f 3(X)	f 4(X)
	0,2 0,9 1,0 1,2 2,0	1,0 1,1 1,3 1,4 1,8	2,1 2,5 2,9 3,9 4,9	2,0 2,5 3,0 4,0

Определите, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль наибольшей.

2. Планируется деятельность трех промышленных предприятий на очередной год. Начальные средства: S ₀=9 условных единиц. Размеры вложения в каждое предприятие кратны 1 условной единице. Средства Х, выделенные k –му предприятию (k =1, 2, 3), приносит в конце года прибыль f_k (X). Функции f_k (X) заданы таблично:

Х	f 1(X)	f 2(X)	f 3(X)

Определите, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль наибольшей.

 

 

Методические указания к практическим занятиям

Линейное и дискретное программирование

Задача. Найти решение ЗЛП

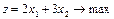
при ограничениях

,

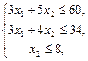
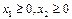Решение. Приведем задачу к каноническому виду, введя дополнительные неотрицательные переменные x₃,, x_4,, x₅. Получим систему ограничений

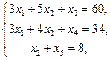
x_j ³0, j=1,2,…,5

Решаем систему симплексным методом поэтапно.

Введем основные (базисные, связанные) и неосновные (свободные, принимающие нулевые значения) переменные. Базисные переменные выразим через неосновные.

1 шаг. Основные переменные x₃, x₄, x₅; неосновные переменные x ₁, x ₂.

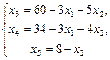
Первое базисное решение: X₁ (0;0;60;34;8) – допустимое. Соответствующее значение линейной функции z₁=0.

Переводим в основные переменную x ₂, которая входит в выражение линейной функции с наибольшим положительным коэффициентом. Находим максимально возможное значение переменной x ₂, которое «позволяет» принять система ограничений, из условия минимума соответствующих отношений:

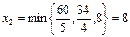
т.е. разрешающим (выделенным) является третье уравнение. При x ₂=8 в этом уравнении x ₅=0, и в неосновные переходит переменная x ₅.

2 шаг. Основные переменные x ₂, x ₃, x ₄; неосновные переменные x ₁, x ₅

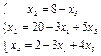
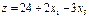
Первое базисное решение: X₂ (0;8;20;2;0) – допустимое. Соответствующее значение линейной функции z₂=24. Переводим в основные переменную x ₁,

,

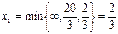а в неосновные x ₄.

3 шаг. Основные переменные x ₁, x ₂, x ₃; неосновные переменные x ₄, x ₅.

.

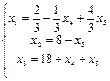
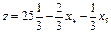X₃ (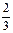;8;18;0;0);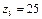

Базисное решение X₃ оптимальное для задачи.

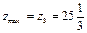(), так как в выражении линейной функции отсутствуют неосновные переменные с положительными коэффициентами.

Задача. Решить задачу Z = 3 x₁ + x₂ ® max при ограничениях:

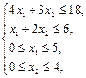
х ₁, х ₂ – целые числа.

Решение. За нижнюю границу линейной функции примем, например, ее значение в точке (0,0), т.е. Z₀= Z(0; 0) = 0.

I этап. Решая задачу симплексным методом, получим Z_max=13 при 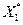= (4,5; 0; 0; 1,5; 0,5; 4); так как первая компонента 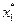дробная, то из области решения исключается полоса, содержащая дробное оптимальное значение 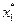, т.е. 4< x ₁<5. Поэтому задача 1 разбивается на две задачи 2 и 3:

Задача 2	Задача 3
Z = 3 x1 + x2 ® max при ограничениях: 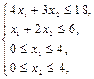х 1, х 2 – целые числа.	Z = 3 x1 + x2 ® max при ограничениях: 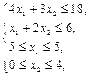х 1, х 2 – целые числа.

Список задач: 2 и 3. Нижняя граница линейной функции не изменилась: Z₀=0.

II этап. Решаем (по выбору) одну из задач списка, например задачу 3 симплексным методом.

Получим, что условия задачи 3 противоречивы.

III этап. Решаем задачу 2 симплексным методом. Получим 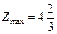при . Хотя 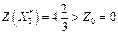, по-прежнему сохраняется Z₀=0, ибо план Х₃ нецелочисленный. Так как 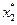- дробное число, из области решений исключаем полосу 0< x ₂<1 и задачу 2 разбиваем на две задачи 4 и 5.

Задача 4	Задача 5
Z = 3 x1 + x2 ® max при ограничениях: 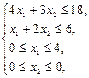х 1, х 2 – целые числа.	Z = 3 x1 + x2 ® max при ограничениях: 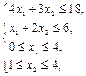х 1, х 2 – целые числа.

Список задач: 4 и 5. Значение Z₀=0.

IV этап. Решаем задачу 4 симплексным методом. Получим Z_max = 12 при = (4; 0; 2; 2; 0; 0). Задачу исключаем из списка, но при этом меняем Z₀; Z₀= Z()=12, ибо план целочисленный.

V этап. Решаем задачу 5 симплексным методом. Получим Z_max = 12,25 при 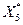=(3,75; 1; 0; 0,25; 0,25; 0; 3). Z₀ не меняется, т.е. Z₀=12, ибо план 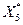нецелочисленный. Так как 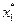- дробное, из области решений исключаем полосу 3< x ₁<4 и задача 5 разбивается на две задачи: 6 и 7.

Задача 6	Задача 7
Z = 3 x1 + x2 ® max при ограничениях: 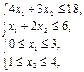х 1, х 2 – целые числа.	Z = 3 x1 + x2 ® max при ограничениях: 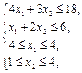х 1, х 2 – целые числа.

Список задач: 6 и 7. Значение Z₀=12.

VI этап. Решаем одну из задач списка, например задачу 7, симплексным методом.

Получим, что условия задачи 7 противоречивы.

VII этап. Решаем задачу 6 симплексным методом. Получим Z_max = 10,5 при 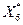=(3; 1,5; 1,5; 0; 0; 0,5; 2,5). Так как Z(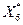)=10,5 < Z₀=12, то задача исключается из списка.

Итак, список задач исчерпан и оптимальным целочисленным решением исходной задачи будет Х* = = (4; 0; 2; 2; 0; 0), а оптимум линейной функции Z_max =12.

ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

Задача. Планируется деятельность четырех промышленных предприятий (системы) на очередной год. Начальные средства: S₀=5 условных единиц. Размеры вложения в каждое предприятие кратны 1 условной единице. Средства Х, выделенные k–му предприятию (k=1, 2, 3, 4), приносит в конце года прибыль f_k(X). Функции f_k(X) заданы таблично:

 

Х	f1(X)	f2(X)	f3(X)	f4(X)

Принято считать, что:

а) прибыль f_k(X) не зависит от вложенных средств в другие предприятия;

б) прибыль от каждого предприятия выражается в одних условных единицах;

в) суммарная прибыль равна сумме прибылей, полученных от каждого предприятия.

Определить, какое количество средств нужно выделить каждому предприятию, чтобы суммарная прибыль наибольшей.

Решение. Обозначим через X_k количество средств, выделенных k-му предприятию. Суммарная прибыль равна 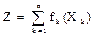. Переменные X удовлетворяют ограничениям: 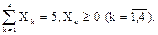Требуется найти переменные X₁, X₂, X₃, X₄, удовлетворяющие данным ограничениям и обращающие в максимум функцию Z.

Рассмотрим особенности модели. Ограничения линейные, но переменные целочисленные, а функции f_k(X_k) заданы таблично, поэтому нельзя применить методы целочисленного линейного программирования.

Схема решения задачи методом ДП имеет следующий вид: процесс решения распределения средств S₀=5 можно рассматривать как 4-шаговый, номер шага совпадает с номером предприятия; выбор переменных X₁, X₂, X₃, X₄ – уравнения соответственно на I, II, III, IV шагах; Ŝ - конечное состояние процесса распределения – равно нулю, так как все средства должны быть вложены в производство, Ŝ=0. Покажем схему распределения:

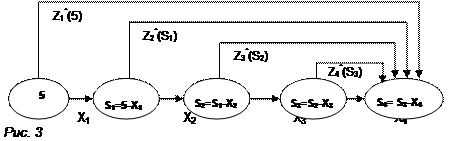Уравнения состояний в данной задаче имеют вид:

S_k=S_k-1-X, (k= ),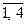

где S_k-параметр состояния – количество средств, оставшихся после k-го шага, т.е. средства, которые остается распределить между оставшимися 4-k предприятиями.

Введем в рассмотрение функцию Z_k^* (S_k-1) – условно оптимальную прибыль, полученную от k-го, (k+1)-го,..., 4-го предприятий, если между ними распределялись оптимальным образом средства S_k-1 (0 £ S_k-1 £ 5). уравнения на k-ом шаге удовлетворяют условию: 0 £ X_k£S_k-1 (либо k-му предприятию ничего не выделяем, X_k=0, либо не больше того, что имеем к k-му шагу, X_k £ S_k-1).

Уравнения (1) и (4) имеют вид:

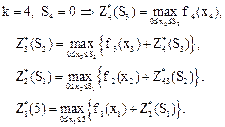
Последовательно решаем данные уравнения, проводя последовательную оптимизацию каждого шага.

IV шаг. Из таблицы условия видно, что f₄(x) прибыли монотонно возрастают, поэтому все средства, оставшиеся к IV шагу, следует вложить в 4-е предприятие. При этом для возможных значений S₃=0,1,..., 5 получим: Z₄^*(S₃)=f₄(S₃) и X₄^*(S₃)=S₃.

III шаг. Делаем все предположения относительно остатка средств S₂ к III шагу: S₂ может принимать значение 0, 1, 2, 3, 4, 5 (например, S₂=0, если все средства отданы 1-му и 2-му предприятиям, S₂=5, если 1-е и 2-е предприятие ничего не получили и т.д.). В зависимости от этого выбираем 0 £ X₃£S₂ и сравниваем для разных X₃, при фиксированном S₂ значения суммы f₃(X₃)+Z₄^*(S₃). Для каждого S₂ наибольшее из этих значений есть Z₃^*(S₂)- условная оптимальная прибыль, полученная при оптимальном распределении средств S₂ между 3-м и 4-м предприятиями. Оптимизация дана в таблице при k=3. Для каждого значения S₂ Z₃^*(S₂) и Х₃^*(S₂) помещены в графах 5 и 6 соответственно.

Sk-1

Xk

Sk

k=3

k=2

k=1

f3(X3)+ Z4*(S3)

Z3* (S2)

X3* (S2)

f2(X2)+ Z3*(S2)

Z2* (S1)

X2* (S1)

f1(X1)+ Z2*(S1)

Z1* (S0)

X1* (S0)

0+1=1 3+0=3

0+4=4 6+0=6

0+6=6 8+0=8

0+6=6 3+4=7 4+0=4

0+7=7 6+4=10 9+0=9

0+10=10 8+6=14 10+0=10

0+8=8 3+6=9 4+4=8 7+0=7

0+9=9 6+7=13 9+4=13 11+0=11

0+13=13 8+10=18 10+6=16 11+0=11

0+13=13 3+8=11 4+6=10 7+4=11 11+0=11

0+13=13 6+9=15 9+7=16 11+4=15 13+0=13

0+16=16 8+13=21 10+10=20 11+6=17 12+0=12

0+16=16 3+13=16 4+8=12 7+6=13 11+4=15 18+0=18

0+18=18 6+13=19 9+9=18 11+7=18 13+4=17 15+0+15

0+19=19 8+16=24 10+13=23 11+10=21 12+6=18 18+0=18

II шаг. Условная оптимизация проведена в таблице при k=2. Для всех возможных значений S₁ значения Z₂^*(S₁) и X₂^*(S₁) находятся в столбцах 8 и 9 соответственно; первые слагаемые в столбце 7 – значения f₂(X₂) взяты из условия, а вторые слагаемые взяты из столбца 5 при S₂=S₁–X₂.

I шаг. Условная оптимизация проведена в таблице при k=1 для S₀=5. Если X₁=0, то S₁=5, прибыль, полученная от четырех предприятий при условии, что S₁=5 ед. средств между оставшимися тремя предприятиями будут распределены оптимально, равна f₁(0)+ Z₂^*(5)=0+19=19. Если X₁=1, то S₂ =4. Суммарная прибыль при условии, что S₂ =4 ед. средств между оставшимися тремя предприятиями будут распределены оптимально, равна f₁(1)+Z₂^*(4)=8+16=24. Аналогично при X₁=2, S₂ =3 и f₁(2)+ Z₂^*(3)=10+13=23; при X₁=3, S₂ =2 и f₁(3)+ Z₂^*(2)=11+10=21; при X₁=5, S₂ =0 и f₁(5)+ Z₂^*(0)=18+0=18. Сравнивая полученные значения, получим Z₁^*(5)=24 усл. ед. = Z_max при X₁^*= X₁^*(5)=1.

Вычисляя, получим S₁^* = 5 - 1 = 4, а по таблице в столбце 9 находим X₂^* = X₂^* (4) = 2. Далее находим S₂^* = 4-2 = 2, а в столбце 6 X₃^* = X₃^*(2) = 1. Наконец, S₃^* = 2-1 = 1 и X₄^* = X₄^*(1) = 1, т. е. X^*(1; 2; 1; 1).

Максимум суммарной прибыли равен 24 усл. ед. средств при условии, что 1-му предприятию выделено 1 усл. ед.; 2-му предприятию – 2 усл. ед.; 3-му предприятию – 1 усл. ед.; 4-му предприятию – 1 усл. ед. ТЕОРИЯ ИГР
Задача. В новом жилом микрорайоне создается ателье для ремонта в стационарных условиях
заявок на ремонт телеаппаратуры выражается (примерно) числами 2, 5, 8, 10 тысяч заявок
в год. Накопленный опыт работы аналогичных предприятий показывает, что прибыль от ремонта одного телевизора
в условиях ателье (ремонт на дому не учитывается) составляет
9 денежных единиц; потери, вызванные отказом в ремонте ввиду недостатка мощностей - 5
денежных единиц; убытки от простоя специалистов и оборудования при отсутствии заявок
6 денежных единиц.
Составить матрицу эффективности работы создаваемого ателье при любом стечении об-
стоятельств. Дать рекомендации о мощности нового ателье. Решение.
Составим матрицу эффективности работы создаваемого ателье.
Обозначим множество стратегий X = {2,5,8,10} - мощности ателье, которые могут быть
выбраны для ремонота телевизоров в микрорайоне. Обозначим S = {0,2,5,8,10}- состояния
среды, возможная потребность в ремонте телеаппаратуры в микрорайоне.
							Заполним ячейку таблицы, выделенную цветом.
X S							Мощность ателье 8 тыс.
	-12			-12	-22		телевизоров в год. Потребность - 5
	-30						тыс. в год. Доход составит 9х5=45 тыс
	-48	-18					Убыток из-за простоя составит 6х3=18
	-60	-30					тыс. Вписываем в эту клеточку 45 - 18=
							27 тыс. единиц в год. Возьмем сосед-
нюю клеточку: мощность ателье 5 тыс. а потребность - 8 тыс. телевизоров в год. Доход соста-
вит 9х5=45 тыс. единиц. Потери, вызванные отказом в ремонте, составят 5х3=15 тыс. Вписы-
ваем в эту клеточку 45 - 15 = 30 тыс. единиц. Действуя аналогичным образом, заполним все
клеточки таблицы.
Приступаем к принятию решения в условиях неопределенности.
Критерий Вальда (критерий осторожного наблюдателя).
Этот критерий оптимизирует полезность в предположении, что среда находится в самом
невыгодном для наблюдателя состоянии. Обозначимlij значение, стоящее в клеточке на пере-
сечении i-ой строки и j-того столбца. Тогда критерий Вальда запишем так:
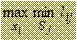
Критерий в таком виде называется максиминными используется в случае поиска наилучшей
стратегии в наихудших условиях, когда речь идет, как в данном случае, о выигрыше. Если выбирается
наилучшая стратегия в случае оценки потерь, то применяется минимаксный критерий
	X S						min
opt		-12			-12	-22	-22
		-30					-30
		-48	-18				-48
		-60	-30				-60
							-22	max
Сначала определяем минимальное значение по каждой строке с помощью функции МИН.
Затем определяем максимальное значение из них с помощью функции МАКС. Таким образом,
по критерию Вальда следует строить телеателье с мощностью 2 тыс. телевизоров в год.
Критерий Лапласа
Если неизвестны состояния среды, то все состояния среды считают равновероятными:
В данном случае число состояний среды равняется J=5 по числу столбцов изучаемой таблицы
Из формулы следут, что каждую строку следует просуммировать и разделить на 5.
Проделаем это
	X S
		-12			-12	-22	-5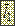
		-30
opt		-48	-18
		-60	-30
						max
По критерию Лапласа следует строить телеателье с мощностью 8 тыс. ремонтов телевизоров в год.
Критерий Гурвица
Критерий основан на следующих предположениях: среда может находится в самом невы-
годном состоянии с вероятностью 1 - α и в самом выгодном с вероятностью α, где α - коэффи-
циент доверия. Тогда решающее правило записывается так:
Еслиα = 0, получаем критерий Вальда.
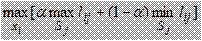
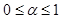
Если α = 1, то приходим к решающему правилу вида
	X S
		-12			-12	-22
		-30
		-48	-18
		-60	-30
	X α	0,1	0,2	0,5	0,9	max	min
		-18	-14	-2			-22
		-22,5	-15	7,5	37,5		-30
		-36	-24				-48
		-45	-30				-60
	max	-18	-14
Оптимальная мощность телеателье в зависимости от αпредставлена в таблице
	α	0,1	0,2	0,5	0,9
	Xopt
Критерий Сэвиджа(минимизации "сожалений").
"Сожаление" или риск есть разность между наилучшим значением в столбце j и всеми осталь-
ными значениями lij в том же столбце. Пусть
Вычитаем это значение из всех остальных в этом столбце:
Строим матрицу "сожалений".
	X S
		-12			-12	-22
		-30
		-48	-18
		-60	-30
	max	-12
	X S						min
				-42	-84	-112	-112
		-18	-18		-42	-70	-70
Xopt		-36	-36	-18		-28	-36
		-48	-48	-30	-12		-48
						max	-36
В случае, если речь идет о потерях, то используется минимаксный критерий.
Подведем итог нашего исследования:
Инвестиции вкладываются по критерию Вальда в сторительство телеателье на2 тыс.ремон-
тов в год.
По критерию Лапласа следует строить телеателье на 8 тыс. ремонтов телевизоров в год.
По критерию Гурвица следует строить телеателье на 2 тыс. ремонтов телевизоров в год, если.
обстановка не внушает доверия, и 10 тыс. - если обстановка благоприятная.
По критерию Сэвиджа следует строить телеателье на 8 тыс. ремонтов телевизоров в год.
Резюме.
Если даже минимальный риск недопустим, следует применять критерий Вальда.
Если наоборот, определенный риск вполне приемлем и заказчик намерен вложить в предпри-
ятие столько средств, чтобы потом не сожалеть, что вложено слишком мало, то выбирают

СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ

Задача. В вычислительный центр коллективного пользования с тремя ЭВМ поступают заказы от предприятий на вычислительные работы. Если работают все три ЭВМ, то вновь поступающий заказ не принимается, и предприятие вынуждено обратиться в другой вычислительный центр. Среднее время работы с одним заказом составляет 3 ч. Интенсивность потока заявок 0,25 (1/ч). Найти предельные вероятности состояний и показатели эффективности работы вычислительного центра.

Решение. По условию n=3, λ=0,25(1/ч), 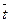_об.=3 (ч). Интен­сивность потока обслуживаний μ=1/ 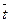_об.=1/3=0,33. Интенсив­ность нагрузки ЭВМ по формуле (24) ρ=0,25/0,33=0,75. Найдем предельные вероятности состояний:

по формуле (25) p₀=(1+0,75+0,75²/2!+0,75³/3!)^-1=0,476;

по формуле (26) p₁=0,75∙0,476=0,357; p₂=(0,75²/2!)∙0,476=0,134; p₃=(0,75³/3!)∙0,476=0,033 т.е. в стационарном режиме ра­боты вычислительного центра в среднем 47,6% времени нет ни одной заявки, 35,7% — имеется одна заявка (занята одна ЭВМ), 13,4% — две заявки (две ЭВМ), 3,3% времени — три заявки (заняты три ЭВМ).

Вероятность отказа (когда заняты все три ЭВМ), таким обра­зом, P_отк.=p₃=0,033.

По формуле (28) относительная пропускная способность центра Q = 1-0,033 = 0,967, т.е. в среднем из каждых 100 заявок вычислительный центр обслуживает 96,7 заявок.

По формуле (29) абсолютная пропускная способность цен­тра A=0,25∙0,967 = 0,242, т.е. в один час в среднем обслуживается 0,242 заявки.

По формуле (30) среднее число занятых ЭВМ 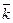=0,242/0,33 = 0,725, т.е. каждая из трех ЭВМ будет занята обслу­живанием заявок в среднем лишь на 72,5/3 =24,2%.

При оценке эффективности работы вычислительного центра необходимо сопоставить доходы от выполнения заявок с потеря­ми от простоя дорогостоящих ЭВМ (с одной стороны, у нас вы­сокая пропускная способность СМО, а с другой стороны — зна­чительный простой каналов обслуживания) и выбрать компро­миссное решение.

Задача. В порту имеется один причал для разгрузки судов. Интен­сивность потока судов равна 0,4 (судов в сутки). Среднее время разгрузки одного судна составляет 2 суток. Предполагается, что очередь может быть неограниченной длины. Найти показатели эффективности работы причала, а также вероятность того, что ожидают разгрузки не более чем 2 судна.

Решение. Имеем ρ = λ/μ = μ 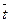_об.=0,4∙2=0,8. Так как ρ = 0,8 < 1, то очередь на разгрузку не может бесконечно возрастать и предельные вероятности существуют. Найдем их.

Вероятность того, что причал свободен, по (33) p₀ = 1 - 0,8 = 0,2, а вероятность того, что он занят, P_зан. = 1—0,2 = 0,8. По формуле (34) вероятности того, что у причала находятся 1, 2, 3 судна (т.е. ожидают разгрузки 0, 1, 2 судна), равны p₁ = 0,8(1-0,8) = 0,16; p₂ = 0,8²∙(1-0,8) = 0,128; p₃ = 0,8³∙(1-0,8) = 0,1024.

Вероятность того, что ожидают разгрузку не более чем 2 судна, равна

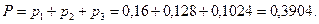
По формуле (40) среднее число судов, ожидающих разгрузки

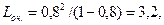
а среднее время ожидания разгрузки по формуле (15.42)

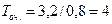(сутки).

По формуле (36) среднее число судов, находящихся у при­чала, L_сист. = 0,8/(1-0,8) = 4 (сутки) (или проще по (37) L_сист. = 3,2+0,8 = 4 (сутки), а среднее время пребывания судна у прича­ла по формуле (41) T_сист = 4/0,8 = 5 (сутки).

Очевидно, что эффективность разгрузки судов невысокая. Для ее повышения необходимо уменьшение среднего времени раз­грузки судна 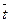_об. либо увеличение числа причалов п.

Задача. В универсаме к узлу расчета поступает поток покупателей с интенсивностью l = 81 чел. в час. Средняя продолжитель­ность обслуживания контролером-кассиром одного покупателя 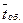= 2мин. Определить:

а. Минимальное количество контролеров-кассиров п_min, при котором очередь не будет расти до бесконечности, и соответст­вующие характеристики обслуживания при n=n_min.

б. Оптимальное количество n_опт. контролеров-кассиров, при котором относительная величина затрат С_отн., связанная с из­держками на содержание каналов обслуживания и с пребывани­ем в очереди покупателей, задаваемая, например, как 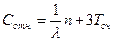, будет минимальна, и сравнить характеристики обслуживания при n=n_min и n=n_опт.

в. Вероятность того, что в очереди будет не более трех покупателей.

Решение.

а. По условию l = 81(1/ч) = 81/60 = 1,35 (1/мин.). По формуле (24) r = l/m = l 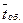= 1,35×2 = 2,7. Оче­редь не будет возрастать до бесконечности при условии r/n < 1, т.е. при n > r = 2,7. Таким образом, минимальное количество контролеров-кассиров n_min = 3.

Найдем характеристики обслуживания СМО при п = 3.

Вероятность того, что в узле расчета отсутствуют покупатели, по формуле (45) p₀ = =(1+2,7+2,7²/2!+2,7³/3!+2,7⁴/3!(3-2,7))^-1 = 0,025, т.е. в среднем 2,5%времени контролеры-кассиры будут простаивать.

Вероятность того, что в узле расчета будет очередь, по (48) P_оч.= (2,7⁴/3!(3-2,7))0,025 = 0,735

Среднее число покупателей, находящихся в очереди, по (50) L_оч. = (2,7⁴/3∙3!(1-2,7/3)²)0,025 = 7,35.

Среднее время ожидания в очереди по (42) T_оч.= 7,35/1,35 = 5,44 (мин).

Среднее число покупателей в узле расчета по (51) L_сист.= 7,35+2,7 = 10,05.

Среднее время нахождения покупателей в узле расчета по(41) T_сист. = 10,05/1,35 = 7,44 (мин).

Характеристика обслуживания	Число контролеров-кассиров
Вероятность простоя кон­тролеров-кассиров p0	0,025	0,057	0,065	0,067

12345

Поделиться:

Воспользуйтесь поиском по сайту: