Главная | Обратная связь | Поможем написать вашу работу!

ДУ, допускающие понижение порядка.

Многочлены над полями Q,R,C. Основная TR алгебры.

Мн-н называется не приводимым над полем Р, если не м. б. представлен в виде произведения двух других мн-нов с коэф-ми из поля Р, степени которых меньше степени данного мн-на.

Мн-н нулевой степени (const) не причисляется ни к приводимым, ни к не приводимым.

Над полем С не приводимы только мн-ны первой степени. Всякий мн-н м/б разложен на лин-ые множители, т.е. всякий мн-н в виде: a₀xⁿ+ a₁xⁿ^-1+…

Над полем R не приводимы только мн-ны 1-ой степени и мн-ны 2-ой степени, не имеющие действит.корней.

Над полем Q существуют не приводимые мн-ны различных степеней.

Пример: xⁿ+2, nєN.

Непроводимость мн-на над Q опр-ся по критерию Эйзенштейна: Если для мн-на n>0 с целыми коэф-ми существует простое число p: старший коэф-т , все остальные коэф-ты , а свободный член , i=1,n. То этот мн-н – не приводим над полем Q.

Пример: 1) x⁴+1 – над Q. 2) x⁴+1= - над R. 3) - над С.

Если степень мн-на > 0 => не разрешимые в радикалах.

Нахождение рацион. Корней мн-на (TR-мы справедливы для мн-нов с целыми коэф-ми):

1)TR1: Если несократимая дробь вида явл-ся корнем мн-на . 2) TR2: Если несократимая дробь вида явл-ся корнем мн-на

3)Следствие из TR2: .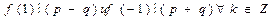

TR1(Основная TR-ма алгебры): Всякий мн-н, степени n>=1 с комплексными коэф-ми, имеет хотя бы 1 корень, в общем случае – комплексный.

TR2: Всякий мн-н, степени n>=1 с комплексными коэф-ми, имеет n корней, если каждый корень считать столько раз, какова его кратность.

TR3: Всякий мн-н f(x) с действительными коэф-ми, имеет комплексный корень а, то и число 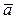также явл-ся его корнем, где кратность а и совпадают.

TR4: Всякий мн-н f(x) с действительными коэф-ми!-ым образом можна представить в виде произведения нескольких множителей вида (x-a), соответ-щих его действ-ым корням, и квадрат-ых 3-членов , соотв-щих его компл-ым корням. При действ-ых значениях а переменной х все указанные множители будут действительными.

Основные типы ДУ 1-го порядка

ДУ – это ур-е, в кот-м неизв. ф-я или в-р ф-и входит под знаком производной или диф-ла.

Порядок ДУ – макс-й порядок входящей в ур-е производной (диф-ла) неизвестной ф-ии.

Ур-я 1-го порядка, разрешаемые относ-но производной.

Обыкн-е ДУ 1-го порядка можно, разрешить относ-но производной, представив в виде:

где с – const. Константа с м. б. определена, если известны знач-я y(x₀)=y₀.

Уравнения с разделенными и разделяющимися пер-ми.

Рассмотрим ДУ вида 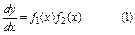Предполагаем, что f₂(у)¹0. преобразуем его к виду Пологая y известной ф-ей от x, (2) можно рассматривать как рав-во 2-х диф-лов, тогда неопределенные интегралы от них будут отличаться постоянным слагаемым С. мы получили соотношение, связывающее искомую ф-ю у, независимую переменную х и произвольную постоянную С, т. е. получили общий интеграл (общ. решение) ур-я (2).

ДУ типа M(x)dx+N(y)dy=0 наз. ДУ с разделенными переменными.

Его общее реш-е имеет вид: , а ур-е вида: М₁(х)N₁(y)dx+M₂(x)N₂(y)dy=0 – наз. ДУ с разделяющимися переменными, т. к. путем деления на М₂(х)N₁(y) оно приводится к ур-ю с разделенными переменными

3. Ур-я, приводимые к ур-ям с разделяющимися пер-ми.

Рассм ур-е вида (1), где - нек. константы. Сделаем замену: , тогда . Подставляя (3) и (2) в (1), получим или - ур-е с разделяющимися пер-ми. Рассм ур-е вида , в этом случае

- ур-е с разделяющимися пер-ми.

4. Линейные ур-я 1-го порядка – ур-я, содержащие у и у^’в первой степени, вида:

Если Q(x)º0 Þ такое ур-е наз-ся однородным его реш-е будет иметь вид: К линейным ДУ могут быть сведены некоторые ДУ:

Уравнение Бернулли

y^’=P(x)y+Q(x)y^m, m¹0, m¹1 Пусть Подставляя полученное выражение в ур-е Бернулли, получим: Пришли к линейному ДУ относительно z.

6. Уравнение Рикатти:

y^’=P(x)y+Q(x)y²+f(x)

В общем виде это ур-е не интегр-ся, но оно может быть сведено заменой пер-х к ур-ю Бернулли, если известно какое-то частное реш-е y₁(x) этого ур-я. Вводя новую ф-ю z(x) пологая y=z+y₁и подставляя последнее в данное ур-е, получим: z’+y₁’= P(x) (z+ y₁)+Q(x)z²+2Q(x)zy₁+ Q(x)y₁ ²+ f(x) т. к. y₁–решение исходного ур-я Þ y₁’=P(x)y₁+Q(x)y₁²+f(x) Подчеркнутые члены взаимно уничтожаются и для отыскания z, получим: z’=(P(x)+2Q(x)y₁)z+Q(x)z², т. е. пришли к ур-ю Бернулли.

7. Уравнения в полных дифференциалах:

– полный дифференциал.

ДУ 1-го порядка вида P(x,y)dx+Q(x,y)dy=0 (1) наз. ур-ем в полных диф-лах, если его левая часть явл-ся полным диф-лом нек-й ф-ии U(x,y), т. е. P(x,y)= Q(x,y)= . Для того, чтобы (1) являлось ур-ем в полных диф-лах необх. и достаточно, чтобы выполнялось след. усл-е:

– условие Эйлера; = =

Если (1)явл-ся. ур-ем в полных диф-лах Þ оно м. б. переписано в виде

dU=0 (2). Общий интеграл (2) имеет вид U(x,y)=C (3), где С – некоторая постоянная. Ф-я U может быть найдена след. образом: по условию имеем =P(x,y). Проинтегрируем это выражение по х

(4). Для отыскания воспользуемся вторым соотношением из условия . Подставим в (4) Þ приходим к ур-ю для отыскания : . Интегрируем, Þ находим подставляя которую в (4), а (4) в (3) закончим процесс построения решения.

ДУ, допускающие понижение порядка.

1. Исходное ДУ не содержит функцию, ее производных до (к-1) порядка т. е. ур-е имеет вид:

F(x,y⁽^k⁾,y⁽^k⁺¹⁾,…y⁽ⁿ⁾)=0 (1)
Порядок ур-я может быть снижен до (n-k)порядка заменой y⁽^k⁾(x)=p(x) Þ y⁽^k⁺¹⁾(x)=p’(x), y⁽^k⁺²⁾(x)=p’’(x)…y⁽ⁿ⁾(x)=p⁽ⁿ^-^k⁾(x) Þ

F(x,p(x),…p⁽ⁿ^-^k⁾(x))=0 (2)
Интегрируя (2) Þ p(x)=p(x,c,…c_n_-_k) Ф-я у после этого находится путём к-ого интегрирования, т. е. y₁⁽^k⁾(x)=p(x, c₁,…,c_n_-_k).

2. Исходное ур-е не содержит переменной x

F(y,y’,…,y⁽ⁿ⁾(x))=0 (3)

В этом случае порядок может быть снижен на 1 подстановкой: y’(x)=p(y), т. е. p рассматривается как новая неизвестная ф-я от y, т. е. p=p(y) Þ y’(x)=p(y) Þ высшие производные будут вычислены по формулам:

y”=(y’)’=(p(y))’=p’y’=pp’ Þ исходное ур-е примет вид F(y,p,p’,…p⁽ⁿ^-1)(y))=0 – порядок ниже на 1.

3. F(x,y,y’,…,y⁽ⁿ⁾(x))=0 и левая часть этого ур-я представляет собой произведение некоторого диф. выражения (n-1) порядка, т. е. j(x,y,y’,…,y⁽ⁿ^-1)(x))=0. В этом случае находится так называемый первый интеграл, т. е. ДУ (n-1) порядка с 1 производной постоянной эквивалентен исходному ур-ю n-го порядка. Этим понижается порядок исходного ур-я на 1.

4. Рассмотрим частный случай ур-я n-го порядка с переменными коэффициентами, именуемые уравнением Эйлера имеет вид:

x⁽ⁿ⁾y_n⁽ⁿ⁾(x)+x⁽ⁿ^-1)y_n_-1⁽ⁿ^-1)(x)+…+xy₁(x)+a₀y(x)=0, a₀=const¹0 (4) Заметим, что порядок х соответствует порядку производной y(x). Решение (4) может быть получено введением новой переменной x=e^t Þ dx=e^tdt (5)

(6)

Аналогично могут быть выражены и следующие производные по x. Подставляя (5), (6) в (4) и преобразуя его, сведём (4) с переменными коэффициентами к ДУ с постоянными коэф-ми, методы решения которые нам известны.

5.F(x,y,y’,…,y⁽ⁿ⁾(x))=0 (7)

Пусть (7) однородно относительно аргумента y,y’,…,y⁽ⁿ⁾ т. е. однородно относительно i-ой производной Þ

F(x,ky,ky’,…,ky⁽ⁿ⁾(x))=k^pF(x,y,y’,…,y⁽ⁿ⁾(x)) (8) (8) является однородным p-го порядка (измерения). Порядок такого ур-я может быть понижен на 1 подстановкой

(9) где z(x) – новая неизвестная ф-я. При такой замене:

y’=z y’’=(z²+z') (10) Подставим (10) в (7) и замечаем в силу однородности (7), что множитель можно вынести за знак ф-ии F и получим

F(x,z,z’,…,z⁽ⁿ^-1)(x))=0.

Воспользуйтесь поиском по сайту: