 |
Отчёт по лабораторным работам №1-2
|
|
|
|
По дисциплине: Технологии визуализации информации
Тема: Создание различных моделей визуализации данных.
Двухмерные и трёхмерные массивы.

Пермь 2016 г.
Цель: ознакомиться с различными вариантами реализации математических моделей и их визуализацией в программной среде MS Excel.
Задачи:
· Имеются две выборки: первая выборка — потребительский спрос на товар А в течение времени, вторая выборка – спрос на товар Б. Требуется выяснить, имеется ли значимое различие между спросом на товары А и Б.
· Располагая данными об изменении температуры с начала отопительного сезона, необходимо построить диаграмму рассеивания.
· Спрогнозировать падение тела на примере определения зависимости высоты от времени свободного падения тела.
· Ознакомиться с другими видами диаграмм и реализовать несколько различных примеров.
Ход работы:
1. В ходе исследования мы получили данные по спросу на товары А и Б.Строим две характеристики на одной плоскости, которые необходимо сравнить между собой, – спрос на товары А и Б. По оси x обозначим время, в течение которого товары находятся на рынке, а по оси y - количество приобретённых товаров. После построения находим такие величины, как:
– Стандартное отклонение.
– Среднее отклонение.
– Среднее значение.
– Среднеквадратическое отклонение.
– Дисперсия.
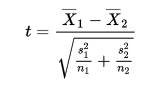 После этого вычисляем t – критерий по формуле:
После этого вычисляем t – критерий по формуле:
который равен 0,631289.
После чего находим степень свободы df = 100+100 – 2 = 198 и определяем по таблице критических значений t – Стьюдента уровень значимости. Значение 0,631289 меньше, чем значения при р ≤0,05 (значение рассчитанного t -критерия Стьюдента меньшетабличного), следовательно, различия между спросом на товары А и Б статистически не значимы.
|
|
|
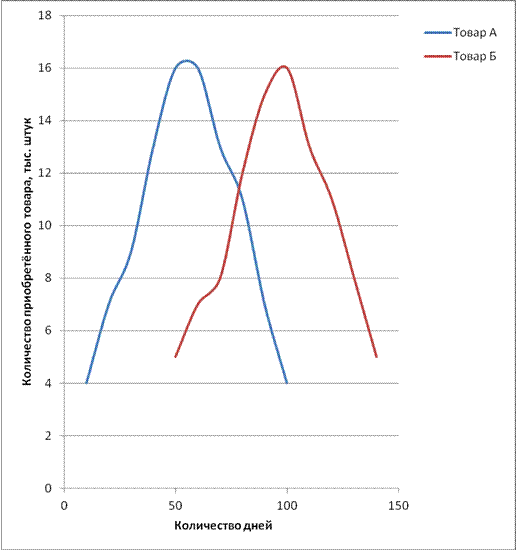
Рисунок 1 – Отображение спроса на товары А и Б
Данная зависимость была построена также с использованием другого типа диаграмм – гистограммы.

Рисунок 2 – Отображение спроса на товары А и Б в виде
гистограмм
2. В ходе выполнения второго пунктанеобходимо построить диаграмму рассеивания с двумя переменными (x – время, y – температура), причём в каждой точке x происходит до 5 измерений. Визуализацию будем проводить при помощи МНК и аппроксимации табличных данных линейной зависимостью.
Для начала мы строим диаграмму рассеивания всех значений y (y1,y2,y3,y4,y5). После чего с помощью функции СРЗНАЧ находим среднее значение (y среднее).
Возьмём приближающую функцию в виде 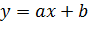 , то есть будем аппроксимировать эту таблично заданную функцию линейной зависимостью.
, то есть будем аппроксимировать эту таблично заданную функцию линейной зависимостью.
В МНК условия минимума можно записать таким образом:
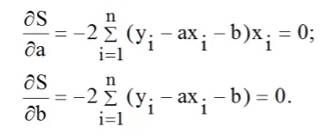
или:

Для отыскания наилучших параметров a и b методом наименьших квадратов, необходимо решить данную систему уравнений. Для этого используем MS Excel.
Решив данную систему матричным методом, используя функции МОБР (получение обратной матрицы) и МУМНОЖ (перемножение обратной матрицы на матрицу свободных членов), мы получаем: a = 1,672308 и b =4,268.
После находим значение y, вычисленное по формуле 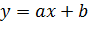 (столбец – y линейное), и строим график. Все проделанные вычисления отображены на рисунке 3.
(столбец – y линейное), и строим график. Все проделанные вычисления отображены на рисунке 3.
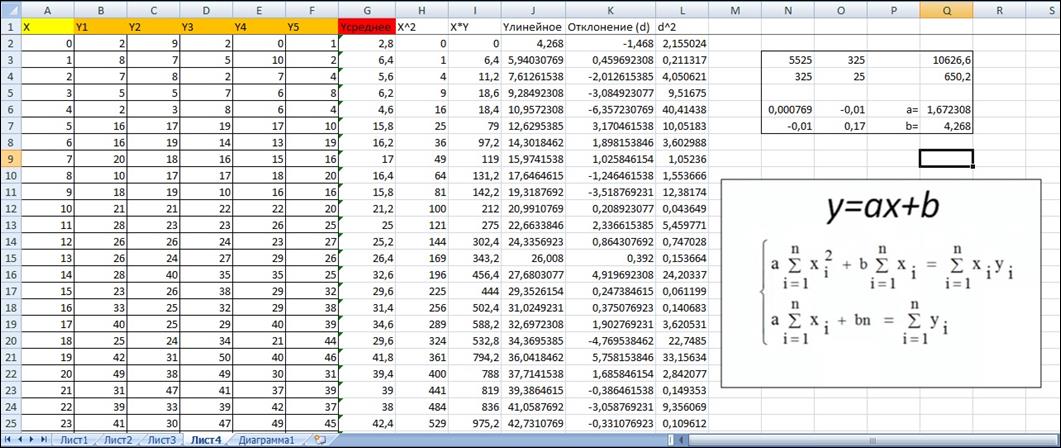
Рисунок 3 – Вычисления с помощью МНК в программной среде MS Excel
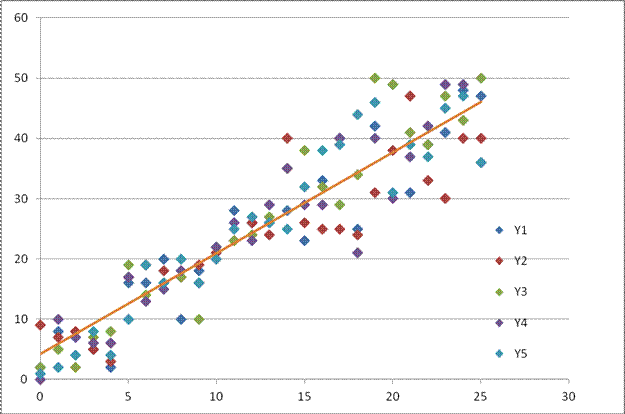
Рисунок 4 – Диаграмма рассеивания, отображающая изменение температуры
3. При помощи аппроксимации возможно спрогнозировать падение тела. Построим диаграмму зависимости высоты от времени свободного падения и аппроксимируем полученную кривую с помощью степенной зависимости.
Как видно, получена следующая аппроксимирующая функция: y =5,0118 x 1,9995.
Теперь по полученной зависимости с помощью MS Excel можно предсказать, например, что за время х =20 сек тело пролетит 1962 м.
|
|
|
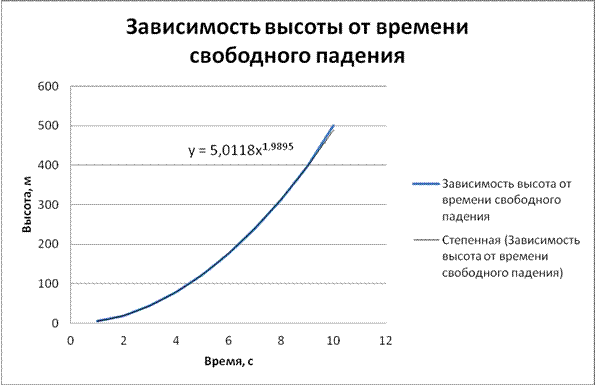
Рисунок 5 – Аппроксимирующая кривая
4. Последним этапом работы является использование различных типов диаграмм для визуализации математических моделей с их обоснованием. Ниже приведены описание задачи и типы диаграмм, которые являются наиболее подходящими для отображения всей полноты информации.

|


Рисунок 6 – Кольцевая диаграмма
Кольцевая диаграмма отображает отношение частей к целому, но может содержать более одного ряда данных. На диаграммах этого типа данные отображаются в виде колец, каждое из которых представляет ряд данных. Если в метках данных отображаются проценты, то каждое кольцо в сумме должно давать 100 %. Такое представление отлично подходит для того, чтобы сравнивать числовые параметры в различных временных промежутках.
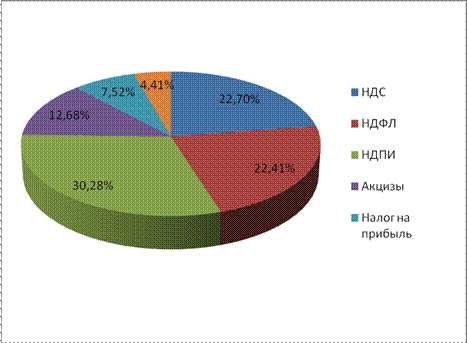
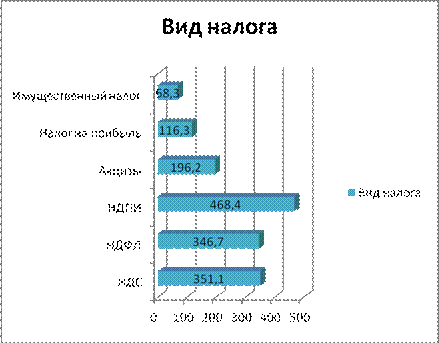
На данных диаграммах в качестве примера взята налоговая аналитика «Поступлений по типам налогов в консолидированный бюджет Российской Федерации за 2015 год» (информация с сайта ФНС).

Рисунок 7 – Линейчатая диаграмма с группировкой
Линейчатые диаграммы иллюстрируют сравнение отдельных элементов. Линейчатые диаграммы с группировкой позволяют сравнивать величины по категориям. В диаграммах этого типа категории обычно располагаются по вертикальной оси, а величины – по горизонтальной.

Рисунок 8 – Объёмная нормированная гистограмма с накоплением
На данной гистограмме изображена динамика продаж автомобилей в период с 2010 по 2015 года.
Данный тип диаграмм подходит, если необходимо сравнивать не одну, а несколько сущностей, которые к тому же дают суммарный вклад в общие итоги.
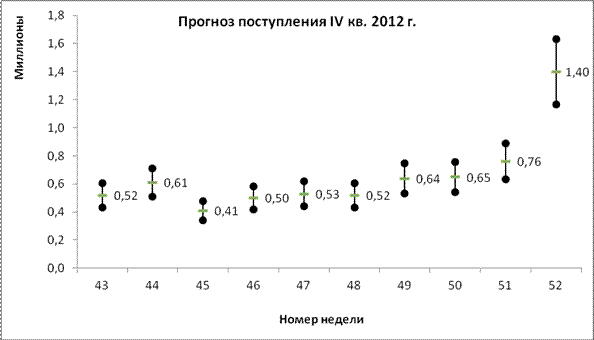
Рисунок 9 – Биржевая (ящичная) диаграмма
Можно выделить следующие области применения ящичных диаграмм:
· Изменение цен акций и объемов торгов.
· Анализ статистических данных (например, в метеорологии или менеджменте качества).
· Представление результатов маркетинговых исследований, социологических опросов.
|
|
|
· Составление прогнозов.
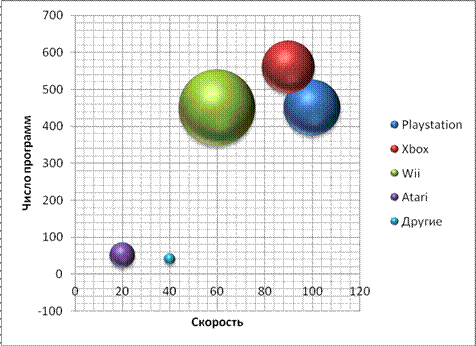
Рисунок 10 – Пузырьковая диаграмма
Данная диаграмма отображает рынок игровых приставок. По оси X представлено быстродействие приставок, по оси Y - число программ для них, доля рынка, занимаемого каждой приставкой, - размер пузырька.
Пузырьковая диаграмма – это разновидность точечной диаграммы, в которой точки данных заменены пузырьками, причем их размер служит дополнительным (третьим) измерением данных.
Таким измерением может являться не только размер пузырька, но и насыщенность его цвета.
Вывод: в ходе выполненной лабораторной работы было произведено ознакомление с различными вариантами реализации математических моделей и их визуализацией в программной среде MS Excel.
|
|
|


