Поток вектора напряженности электрического поля. Теорема Остроградского-Гауса. Циркуляция вектора напряженности электростатического поля. Теорема Ирншоу.

Связь напряженности и потенциала электростатического поля

Будем искать, каким образом связаны напряженность электростатического поля, которая является его силовой характеристикой, и потенциал, который есть его энергетическая характеристика поля.

Работа по перемещению единичного точечного положительного электрического заряда из одной точки поля в другую вдоль оси х при условии, что точки расположены достаточно близко друг к другу и x₂—x₁=dx, равна E_xdx. Та же работа равна φ₁—φ₂=dφ. Приравняв обе формулы, запишем

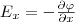(1)

где символ частной производной подчеркивает, что дифференцирование осуществляется только по х. Повторив эти рассуждения для осей у и z, найдем вектор Е:

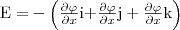
где i, j, k — единичные векторы координатных осей х, у, z.

Из определения градиента следует, что

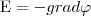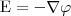или (2)

т. е. напряженность Е поля равна градиенту потенциала со знаком минус. Знак минус говорит о том, что вектор напряженности Е поля направлен в сторону уменьшения потенциала.

Поток вектора напряженности электрического поля. Теорема Остроградского-Гауса. Циркуляция вектора напряженности электростатического поля. Теорема Ирншоу.

По определению потоком векторного поля 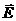через площадку 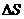называется величина

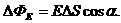
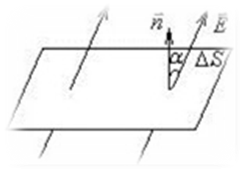
К определению потока вектора .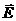

Если поле неоднородно или поверхность, через которую вычисляется поток, не является плоской, то определение потока нужно применить к бесконечно малому элементу поверхности, а именно записать:

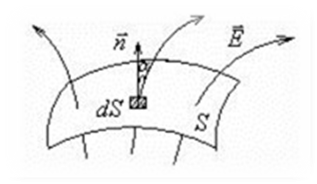
Тогда поток через всю поверхность S будет:

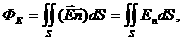
Рис.2.2. где .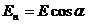

Заметим, что поток – величина алгебраическая. Знак потока зависит от выбора направления нормали к элементарным площадкам, на которые разбивается поверхность S при вычислении ФЕ. Изменение направления нормали на противоположное изменит знак En, а значит и знак потока ФЕ. В случае замкнутых поверхностей принято считать знак потока положительным, если силовые линии поля выходят из охватываемой области наружу. Численно поток равен количеству силовых линий, пресекающих данную поверхность. Размерность потока в СИ: [ФЕ] = В·м (отметим, что она совпадает с размерностью величины q/εо).

Окружим точечный заряд q замкнутой сферической поверхностью радиусаr и вычислим поток электрического поля точечного заряда через эту поверхность (рис.2.3).

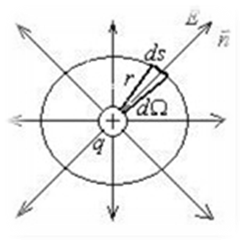По определению имеем: ,

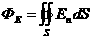где 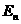- напряженность электрического поля в направлении внешней нормали, 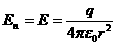; 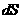- элемент поверхности, , - элемент телесного угла.

К доказательству теоремы Гаусса.

Вычисляем: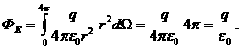

Мы видим, что полученный результат не зависит от формы и размеров выбранной поверхности. Это очевидно, поскольку поток численно равен количеству силовых линий, пересекающих данную поверхность, и в случае выбора замкнутой поверхности любой другой формы он не изменится, так как силовые линии нигде не прерываются.

Если внутри замкнутой поверхности имеется несколько зарядов, то поток их результирующего поля, согласно принципу суперпозиции, будет равен:

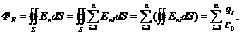
В частности, если система зарядов находится вне выбранной поверхности или алгебраическая сумма всех зарядов, заключенных под поверхностью, равна нулю, то поток .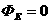

Доказанная выше теорема, носит название теоремы Гаусса (Полная ее формулировка звучит так: поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности (деленной на ):

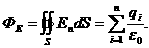
Отметим, что теорема Гаусса является прямым следствием закона Кулона и является одной из основных теорем электростатики.

 

В случае, если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль какой-либо траектории (рис. 1) двигается другой точечный заряд Q₀, то сила, которая приложена к заряду, совершает некоторую работу. Работа силы F на элементарном перемещении d l равна

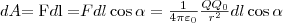
Так как d l /cosα=dr, то

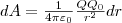
Работа при перемещении заряда Q₀ из точки 1 в точку 2

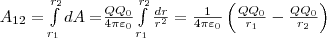(1)

от траектории перемещения не зависит, а определяется только положениями начальной 1 и конечной 2 точек. Значит, электростатическое поле точечного заряда является потенциальным, а электростатические силы — консервативными

Из формулы (1) видно, что работа, которая совершается при перемещении электрического заряда во внешнем электростатическом поле по произвольному замкнутому пути L, равна нулю, т.е.

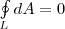(2)

Если в качестве заряда, которого перемещают в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути d l равна Е d l = E _l d l, где E _l = Ecosα — проекция вектора Е на направление элементарного перемещения. Тогда формулу (2) можно представить в виде

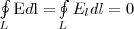(3)

Интеграл называется циркуляцией вектора напряженности. Значит, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, которое обладает свойством (3), называется потенциальным. Из равенства нулю циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они обязательно начинаются и кончаются на зарядах (на положительных или отрицательных) или же идут в бесконечность.

Формула (3) верна только для электростатического поля. В дальнейшем будет показано, что с случае поля движущихся зарядов условие (3) не верно (для него циркуляция вектора напряженности отлична от нуля).

 

Поделиться:

Воспользуйтесь поиском по сайту: