Устойчивость тонкостенных стержней

УСТОЙЧИВОСТЬ ПЛАСТИНОК

 

Пластинка является наиболее характерным элементом конструкции самолёта и двигателя. С ней обычно отождествляют элемент обшивки крыла, фюзеляжа, оперения летательного аппарата, стенку лонжерона, нервюры, шпангоута.

Основной особенностью пластинки является её способность воспринима-ть только распределённую нагрузку, действующую главным об­разом в её плоскости, (рис. 11.1)

Обычная пластинка при дейст­вии распределенной поперечной нагрузки работает как широкополая; балка сплошного поперечного сечения, но при этом наблюдаются две особенности:

- при изгибе из-за стеснения поперечных деформаций пластинка оказывается несколько более жест­кой, чем узкая балка той же площади

цилиндрическая жёсткость - выше обычной ;

Рис. 11.1. Нагружение пластины - граничные условия для пластинки более разнообразны, так как включают опирание продольных кромок (рис. 11.2), свободных у балки.

Распределённую попе-речную нагрузку пластинка воспринимает плохо и в этом отношении не является рациональным элементом, по­скольку работает на изгиб. По этой причине пластинке присущи все недостатки балки сплошного попереч-ного сечения. Обычно применяют пластинки, под-креплённые рёбрами жёсткости (стрингерами, Рис. 10.2. Схемы опирания пластины нервюра­ми) - панели.

Значительно лучше пластинка работает на восприятие нагрузок, прило-женных в её плоскости (растяжение, сжатие, сдвиг).

При растяжении пластинки разрушаются при достижении в материа­ле напряжений уровня σ_b (предел прочности при растяжении).

При сжатии и сдвиге пластинки разрушаются из-за потери устой­чивости. Нагрузки инапряжения, действующие в момент потери устойчивости, принято называть критическими.

Рассчитать величину указанных напряжений можно с использовани­ем дифференциального уравнения продольно-поперечного изгиба.

 

11.1. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ПОПЕРЕЧНОГО
ИЗГИБА ПЛАСТИНЫ.

При условии выполнения для материала закона Гука уравнение имеет вид:

(11.1)

 

где: W, D- прогиб и цилиндрическая жесткость пластинки;

D - распределённая по площади поперечная нагрузка;

N _x - распределённые по ширине пластинки погонные усилия;

n_y - распределённые по длине пластинки погонные усилия;

q- погонные касательные усилия.

Решение дифференциального уравнения (11.1) заключается в нахож­дении такой функции W(x,y), которая в каждой точке, взятой внутри пластинки, обращает данное уравнение в верное равенство, ана контуре удовлетворяет ещё и граничным условиям (11.2).

Рассмотрим решение дифференциального уравнения (11.1) в упрощён­ном виде при действии распределённой сжимающей нагрузки только в
направлении оси X (рис. 11.3). Граничные условия - шарнирное опирание по
4-м кромкам (рис. 11.2, в).

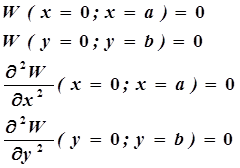(11.2)

Рис.11.3 Нагружение и опирание сжатой пластинки

Применим метод подбора решения. Можно проверить, чтопо край­ней мере граничным условиям (1.2в) удовлетворяет функция:

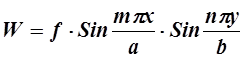(11.3)

 

где m и п - целые числа I, 2 …

f - некоторый коэффициент.

Эта же функция похожим образом описывает и форму поверхности пластинки после потери устойчивости.

Будем поэтому считать (11.3) приближённым решением (11.1). Нас будет интересовать вопрос, при каких значениях нагрузки начальная форма плоского равновесия перестаёт быть устойчивой (w¹ 0)

Для этого в дифференциальное уравнение (11.1) подставим (11.3).

Подготовим значения производных для подстановки.

 

Результаты подстановки после сокращения на общий множитель

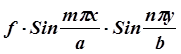
После очевидных преобразований имеем:

и

 

Обычно n = 1 (вдоль оси y образуется только одна полуволна), поэтому

.

Учитывая, что

имеем

.

 

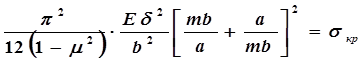Величина

,

 

а величина 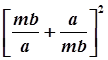обозначается как k _s.

 

Окончательно 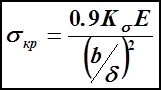(11.5)

График функции К σ = f(а/b)для различных форм потери устой­чивости при шарнирном опирании по 4кромкам приведен на рис.1.4.

Рис. 11.4. График функции Кσ = f(а/b)

Реализуется всегда наименьшее значение критических напряжений, отсюда всегда можно определить заранее, по какой форме пластинка потеряет устойчивость, если её размеры известны.

При пользовании формулой (11.5) следует учитывать, что небез­различно, как ориентирована пластинка в системе координат X, У. Размер "а" следует брать внаправлении действующей сжимающей на­грузки (Рис.11. 4).

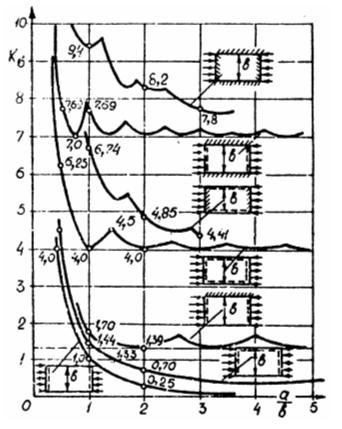В случае других форм опира-ния следует пользоваться специаль-ными таблицами и графиками, в частности, графиком, приведенным на рис. 11.5.

11.2. КРИТИЧЕСКИЕ
НАПРЯ ЖЕНИЯ СДВИГА

Аналогично тому, как было получено выражение для критичес-ких напряжений сжатия, можно получить выражения для критических напряжений сдвига.

Для этого в уравнении(11.1) следует справа удер­жать только член , остальные принять равными 0.

 

 

Рис. 11.5. График функции Кσ = f(а/b) для

Различных форм опирания

Результат решения:

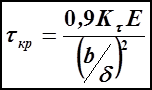(11.6)

 

Размер " b " при использовании (11.6) - всегда наименьший.

Величина К_τ, такжекак и К_σ для различных, случаев опирания пластинки по контуру берётся из таблиц, для наиболее употребительного случая - шарнирного опирания по 4-м кромкам, может рассчитываться по. формуле:

Физическая картина потери устойчивости при сдвиге иллюстриру­ется на рис. 11.6.

Сдвиг - это плоское напряжённое состояние, которое в окрестности каж­дой точки пластинки можно представить комбинацией растяжения и сжатия по 2-м взаимно перпендикулярным направлениям. Напряжения по обеим главным площадкам одинаковы по модулю σ₁ = - σ₂

Потеря устойчивости происходит под действием сжимающих напряжений σ₂, поэтому гребни волн образующихся при этом, направлены под углом 45° к основанию пластинки.

Рис. 11.6. Потеря устойчивости пластины при сдвиге

11.3. КРИТИЧЕСКИЕ НАПРЯЖЕНИЯ ПРИ СОВМЕСТНОМ
ДЕЙСТВИИ СЖАТИЯ И СДВИГА

Совместное действие сжатия и сдвига наблюдается при одновременном изгибе и кручении крыла, фюзеляжа, оперения и т.д.

При этом каждый элемент обшивки опёртый на два соседних стрингера и две нервюры, работает на сжатие, растяжение и сдвиг. Наиболее опасна комбинация сжатия и сдвига, т.к. растяжение способству­ет повышению критических напряжений. Общее решение можно получить, удерживая в правой части дифференциального уравнения (1I.I) члены и

Оно имеет вид

(11.8)

 

где σ_кр, τ_кр - критические напряжения сжатия и сдвига при их раздельном совместном действии,

n = 1…2 (обычно для алюминиевых сплавов n = 1,7).

Одно из напряжений (σ или τ) должно быть задано как действующее, второе определяется.

11.4. КРИТИЧЕСКИЕ НАПРЯЖЕНИЯ ПЛАСТИНКИ,
РАБОТАЮЩЕЙ ЗА ПРЕДЕЛА­МИ ПРОПОРЦИОНАЛЬНОСТИ.

Всё сказанное выше о расчёте критических напряжений справед­ливо для случая относительно тонких пластинок, теряющих устойчи­вость в пределах пропорциональности. Толстые пластинки теряют ус­тойчивость за пределом пропорциональности, когда основное допуще­ние, принятое при выводе дифференциального уравнения (11.1) (де­формации материала подчиняются закону Гука), не выполняется. Рас­чёт критических напряжений в этом случае проводятся с использова­нием эмпирических зависимостей:

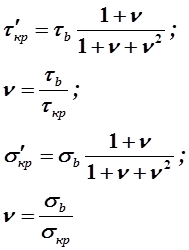(11.9)

где σ_кр и τ_кр определяются обычным способом.

Таким образом, расчёт критических напряжений пластинки вклю­чает в себя этапы:

1. Расчёт σ_кр или τ_кр в предположении работы материала в пределах пропорциональности.

2. Проверка выполнимости принятого предположения.

3. Пересчёт в случае необходимости критических напряжений σ_кр и τ_кр с использованием эмпирических зависимостей (9).

 

ВОПРОСЫ

1. Какие нагрузки хорошо воспринимает пластинка?

2. Опишите способы опирания пластинок?

3. Причины разрушения пластинки при растяжении, сжатии и сдвиге?

4. Укажите, какие параметры входят в дифференциальное уравнение поперечного изгиба пластины? В чем заключается решение этого уравнения? В чем заключается метод подбора решения?

5. Опишите уравнение для определения критического напряжения при сжатии?

6. Опишите график функции К_σ = f (а/b) при шарнирном опирании 4 кромок.

УСТОЙЧИВОСТЬ ТОНКОСТЕННЫХ СТЕРЖНЕЙ

Стержень - элемент удлинённой формы, работающий на растяжение-сжатие от продольных (осевых) сил (рис. 12.1, а).

Стержни в авиационных конструкциях - это стрингеры крыла, фюзеляжа, оперения, пояса лонжеронов, тяги проводки управления и т.д. Они имеют обычно тонкостенные поперечные сечения открытого или замкнутого профиля.

Открытые тонкостенные стержни (рис. 12.1, б) изготавливаются прессованием, прокаткой или штамповкой из тонких листов. их характерными сечениями являются профили уголкового, швеллерного, таврового и двутаврового типа.

 

Рис. 12.1. Примеры стержней, применяемых в авиаконструкциях

Наиболее распространёнными стержнями с замкнутыми се­чениям являются тонкостенные трубы. В ряде случаев замкну­тые сечения получаются после приклёпывания открытого профи­ля к обшивке (рис. 11.1, в).

Особенностью тонкостенных стержней является недоста­точная жёсткость поперечных сечений и возможность их искажения под действием внешней сжимающей силы.

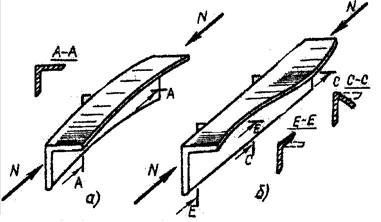Если соотношения размеров стержня таковы, что в про-цессе нагружения не происходит существенного изменения формы и. размеров поперечных сечений, то такой стержень при действии продольной сжимающей силы претерпевает общую потерю устойчивости с изгибом его оси (рис.12.2, а).

Рис.12.2. Виды потери устойчивости поэтому разрушение
тонкостенных стержней длинных изолированных

стержней при сжатии обычно происходит от общей потери устойчивости.

Короткие тонкостенные стержни обладают повышенной изгибной жёсткостью в продольном направлении и при действии сжимающей нагрузки чаще разрушаются в результате выпучивания тонких стенок (рис. 11.2, б) без искривления оси, то есть в результате местной потери устойчивости.

 

12Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: